Существуют матричные модели для описания гранулометрического состава материалов, однако применение их сопряжено с трудоемкими вычислительными процедурами и значительными погрешностями, а также с необходимостью проведения большого количества экспериментов по разрушению одиночных частиц и т. д.
В частности, для обобщения экспериментальных данных по разрушению одиночных частиц и использования их для потока материала необходимо было составлять и решать матрицы в следующем виде [1]:
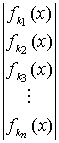 =
= 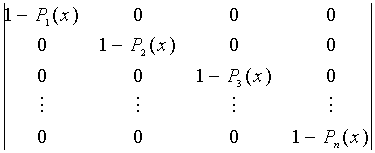 x
x 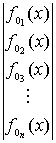 +
+
+ 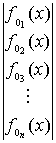 x
x 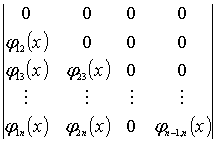 x
x 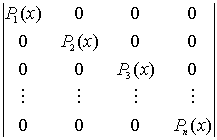 ,
, (1)
(1)
где f0 (x) — исходная монофракция, равная единице;
fkn(x) — приведенная дифференциальная доля в пределах n–ной фракции в конечном гранулометрическом составе;
φ1n(x) — приведенная дифференциальная доля n–ной фракции в распре-делительной функции, показывающая какая часть материала перешла из первой фракции в n–ную.
С учетом этого, для расчета изменения гранулометрического состава дисперсных материалов в настоящей статье предлагается более упрощенная и информативная методика, которая заключается в определении вероятностных параметров перехода непосредственно в потоках частиц, т. е. с использованием только селективной функции, вместо двух — селективной и распределительной.
Сущность данного подхода базируется на материальном балансе полидисперсного потока до и после разрушения, который можно выразить в виде следующей матрицы:
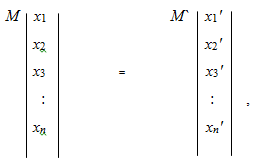 (2)
(2)
где M, M' — массовые расходы потока до и после разрушения (считаем, что M = M`); (х1, х2, х3,…,хn), (х1', х2', х3',…, хn') — соответственно, распределения полидисперсных частиц в потоке до и после разрушения.
Если распределение частиц по размерам представить в весовых долях, то справед-ливо условие: х1+х2+х3+…+хn=1,0и х1'+х2'+х3'+…+хn'=1,0.



 Переход разрушенных частиц из крупных в мелкие фракции при измельчении материалов осуществляется по следующей схеме при условии (х1> х2> х 3>…>хn):
Переход разрушенных частиц из крупных в мелкие фракции при измельчении материалов осуществляется по следующей схеме при условии (х1> х2> х 3>…>хn):
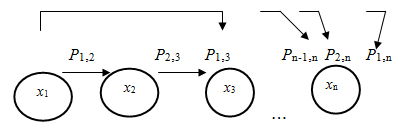
где Р1,2; Р1,3; Р1,n — вероятности перехода частиц из первой фракций, соответственно, во вторую и n-ную фракции;
Р2,3, Р2,n — то же самое, но для частиц последующих фракций.
Вероятность перехода выражается отношением массы частиц, перешедших при разрушении в следующие фракции, к исходной массе фракции. С учетом вероятностей перехода и материального баланса потока, гранулометрический состав частиц после разрушения определяется по следующему выражению:
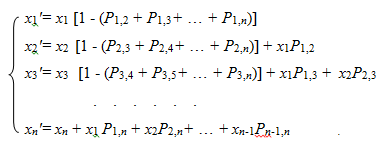 (3)
(3)
В системе уравнений (.3) выражения в квадратных скобках характеризуют доли неразрушившихся частиц, т. е. оставшихся в пределах тех же фракций, в которых они находились, а правые слагаемые — доли частиц, перешедших после разрушения в более мелкие фракции. Отличительной особенностью предложенной методики расчета грану-лометрического состава дисперсных материалов является то, что значительно упрощается механизм вычислений матриц. Вероятности перехода зависят от физико-механических свойств частиц, ее размеров, динамических параметров соударения, и использование предложенной методики позволяет получать вполне надежные результаты.
Литература:
1. Сариев А. А. Экспериментальное исследование изменения гранулометрического состава дисперсного материала при многократных нагружениях // Химия и хим. технология. — 2003.– Т.46, № 5. -С. 162–163.







