Учет нелинейных составляющих в выражениях деформаций оболочки через перемещения координатной поверхности необходим для получения более точных результатов вычислительного эксперимента при расчете конструкций различного назначения. Использование линейных моделей для расчета напряженно-деформированного состояния оболочек вращения дает значительную погрешность при больших нагрузках. При учете геометрической нелинейности эта погрешность значительно уменьшается.
В данной работе представлена численная модель геометрически нелинейного деформирования упругих неортотропных пространственно армированных оболочек вращения, основанная на методе конечных элементов в варианте метода перемещений. Модель построена на основе статических гипотез и кинематических гипотезах типа Кирхгофа-Лява и Тимошенко с использованием вариационных принципов теории оболочек. В качестве узловых неизвестных в первом случае выбраны линейные перемещения и их производные, во втором к ним добавлены углы поворота нормали со своими производными.
Использованные статические гипотезы теории оболочек включают предположения об отсутствии нормальных напряжений, действующих вдоль нормали к координатной поверхности оболочки, и равенстве нулю напряжений поперечного сдвига на лицевых поверхностях. В выражении для энергии деформации напряжения поперечного сдвига считаются пропорциональными квадратичной функции нормальной координаты [1].
В качестве свободных переменных взяты значения линейных и угловых перемещений и их производные. Для модели, основанной на гипотезе Кирхгофа-Лява, угловые перемещения выражаются через остальные переменные [3].
При геометрически нелинейной поставке задачи деформации координатной поверхности оболочки вращения представляются в виде суммы линейной и нелинейной составляющих. Тензор деформаций координатной поверхности содержит восемь компонент, в случае гипотезы Тимошеко, и шесть, в случае гипотезы Кирхгофа-Лява, так как углы поворота нормали в последнем случае не учитываются.
Так как рассматривается вариант осесимметричного нагружения, перемещения и деформации зависят только от меридиональной координаты. В связи с этим нелинейные составляющие учитываются только в выражениях деформаций координатной поверхности в направлении меридиана оболочки [2]:
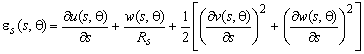(1)
где (s, q) — ортогональная система координат, заданная на координатной поверхности оболочки;
u(s,θ), v(s,θ), w(s,θ) — линейные перемещения координатной поверхности: вдоль дуги, окружности и нормали соответственно;
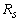— радиус кривизны.
Для задания зависимости перемещений от меридиональной координаты используется интерполяция с помощью эрмитовых сплайнов третьего порядка, что позволяет получить достаточно качественное решение и обеспечивает непрерывность производных от перемещений [3].
Тогда формула для потенциальной энергии элемента выглядит следующим образом [1]:
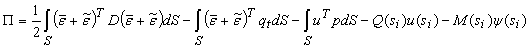, (2)
где S — площадь поверхности элемента;
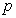– распределенная нагрузка;
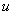— вектор перемещений координатной поверхности;
Q(si), M(si) — сосредоточенные силы и моменты;
si — текущая меридиональная координата;
— вектор углов поворота нормального элемента;
qt — начальные температурные воздействия;
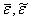— соответственно линейные и нелинейные составляющие тензора деформаций координатной поверхности оболочки.
После суммирования по элементам и дифференцирования по степеням свободы условие минимума потенциальной энергии записывается в виде системы нелинейных алгебраических уравнений:
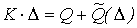, (3)
где K — глобальная матрица жесткости;
Q — глобальный вектор узловых сил;
Δ — глобальный вектор узловых переменных;
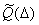— глобальный вектор дополнительных узловых сил:
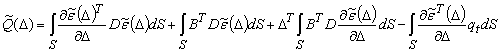. (4)
Процесс решения происходит итерационно [4]. На первой итерации решается система линейных уравнений:
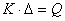. (5)
После этого найденное решение подставляется в вектор дополнительных узловых сил (4), который прибавляется к правым частям уравнений системы. Итерации продолжаются до достижения заданной точности.
По рассмотренному алгоритму была написана программа и проведены вычислительные эксперименты для анализа результатов учета геометрической нелинейности при решении модельных задач.
Результат вычислительного эксперимента, представленный на рисунке 1 свидетельствует о согласовании построенной модели с поведением реальной конструкции. Рассчитывалось напряженно-деформированное состояние полусферической оболочки, изготовленной из изотропного материала с модулем упругости Е=200000МПа и коэффициентом Пуассона ν=0.3. Исследовалась зависимость нормальных перемещений от нагрузок. Модель построена с учетом гипотезы Кирхгофа-Лява. По результатам расчета (см. рисунок 1) видно, что при малых нагрузках (не превышающих 15 МН/м2), значения перемещений, рассчитанных с учетом нелинейных составляющих деформаций совпадают со значениями, рассчитанными без их учета. Начиная с нагрузки 15 МН/м2 разница в результатах расчета заметна, а начиная с 25 МН/м2 при учете геометрической нелинейности сходимость отсутствует; это может быть связано с потерей устойчивости.
Рис. 1. Полусферическая оболочка
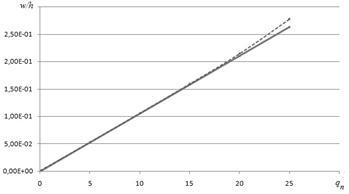
решение задачи в линейной постановке;
решение задачи с учетом геометрической нелинейности
Рис. 2. Зависимость прогибов от нормальных нагрузок полусферической оболочки
Следующий вычислительный эксперимент показал, что уточнение решения, связанное с использованием геометрической нелинейности наиболее заметно при расчетах с использованием классической гипотезы Кирхгофа-Лява, чем с использованием уточненной гипотезы Тимошенко. На рисунке 3 представлены зависимости прогибов от меридиональной координаты с учетом разных гипотез, полученные при расчете напряженно-деформированного состояния цилиндрической оболочки. Конструкция имеет следующие геометрические параметры: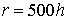 
, 
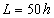, где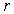 
— радиус, 
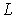— образующая, 
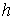— толщина стенки, изготовлена из изотропного материала с модулем упругости =2*105Па и коэффициентом Пуассона 
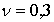. Подвергается воздействию нормальной нагрузки qn=0.2 МН/м2.
а)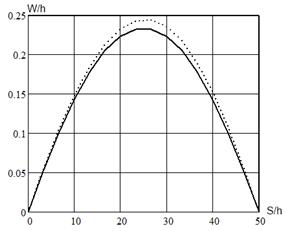
б)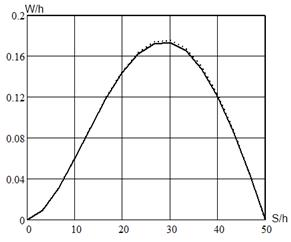 
без учета нелинейных составляющих деформаций;
с учетом нелинейных составляющих деформаций
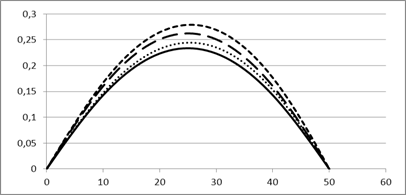
Рис. 3. Нормальные перемещения в цилиндрической оболочке, рассчитанные с учетом: а) гипотезы Кирхгофа-Лява; б) гипотезы Тимошенко
На рисунке 3 явно видно различие результатов вычислительного эксперимента, полученных при применении гипотез Кирхгофа-Лява и Тимошенко. Прогибы, рассчитанные на основе применения классической гипотезы Кирхгофа — Лява (см.рисунок 3, а), больше чем рассчитанные на основе уточненной теории Тимошенко (см. рисунок 3,б). Учет геометрической нелинейности оказал значительное влияние на результат расчетов только при использовании теории Кирхгофа-Лява. В этом случае различия результатов расчетов по линейной и нелинейной модели составляют 5.556 % (см. рисунок 3,а). При использовании модели, основанной на гипотезе Тимошенко значительного уточнения результатов вычислительного эксперимента при учете нелинейных составляющих в выражениях деформаций координатной поверхности не наблюдается (составляет 1.6 %) (см. рисунок 3,б).
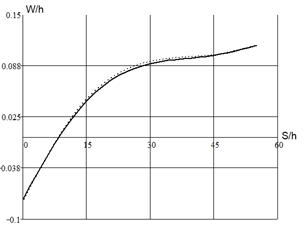
На рисунке 4 представлены результаты исследования поведения этой же цилиндрической оболочки при нагреве на 50С и давлении qn=0.2 МН/м2.
W/h
S/h
без учета нелинейных составляющих деформаций не нагретой оболочки;
с учетом нелинейных составляющих деформаций не нагретой оболочки;
без учета нелинейных составляющих деформаций при нагреве на 50С;
с учетом нелинейных составляющих деформаций при нагреве на 50С
Рис. 4. Прогибы по меридиану цилиндрической оболочки при нагреве на 50С и нормальных нагрузках qn=0.2 МН/м2
По результатам расчета можно сделать вывод, что с ростом температуры разница между перемещениями, рассчитанными с учетом и без учета нелинейных составляющих, увеличивается, что свидетельствует о возрастании значимости нелинейных составляющих деформации.
Проведем расчет напряженно-деформированного состояния оболочки вращения, представляющую собой часть полусферы (см. рисунок 1), изготовленной из изотропного материала с модулем упругости Е=2*105МПа и коэффициентом Пуассона ν=0.3.
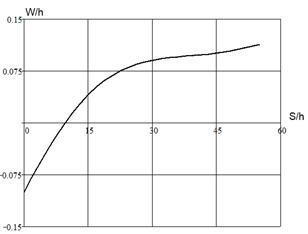
Сравнивались значения прогибов при одновременном воздействии нормального давления qn=10 МН/м2 ирастягивающей нагрузки вдоль меридиана Qs=10 МН/м, и при раздельном воздействии этих нагрузок с последующим сложением векторов перемещений (рисунок 5).
Результаты расчета нормальных перемещений с использованием линейной модели в случаях раздельного воздействии нагрузок с последующим сложением векторов перемещений и их одновременном воздействии полностью совпадают (см. рисунок 5,б), что не соответствует действительности. В случае же учета нелинейных составляющих деформаций заметно различие значений перемещений при раздельном и одновременном воздействии нагрузок (см. рисунок 5,а).
а) б)
при одновременной нагрузке Qs=10 МН/м и qn=10 МН/м2;
при сложении нагрузок Qs=10 МН/м и qn=10 МН/м2по компонентам
Рис. 5. Прогибы по меридиану полусферической оболочки: а) без учета нелинейных составляющих деформаций; б) с учетом нелинейных составляющих деформаций
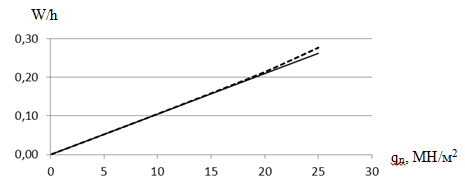
Следующий вычислительный эксперимент заключается в исследовании зависимости перемещений от нагрузок, при варьировании нормальных нагрузок с учетом гипотезы Кирхгофа-Лява. Зависимость перемещений от нагрузок представлена на рисунке 6.
без учета нелинейных составляющих деформаций;
с учетом нелинейных составляющих деформаций
Рис. 6. Зависимость прогибов цилиндрической оболочки от нормального давления
Литература:
1. Решетникова Е. В. Численно-аналитическое моделирование статики, устойчивости и колебаний пространственно армированных оболочек вращения. Автореферат дис. на соискание ученой степени кандидата технических наук: 05.13.18. /Новокузнецк, 2005.
2. Механика композитных материалов и элементов конструкций: В 3-х т. Т.2. Механика элементов конструкций / А. Н. Гузь, Я. М. Григоренко, И. Ю. Бабич и др.– Киев: Наук. Думка, 1983. — 464 с.
3. Сегерлинд Л. Применение метода конечных элементов / Л. Сегерлинд. — М.: Мир, 1979. — 392 с.
4. Еременко С. Ю. Методы конечных элементов в механике деформируемых тел / С. Ю. Еременко. — Харьков: изд. «Основа» при Харьк. гос. ун-те, 1991. — 272 с.
5. Каледин В. О. Напряженно-деформированное состояние подкрепленных и составных ортотропных оболочек вращения [Текст] / В. О. Каледин, Е. В. Решетникова // Вопросы оборонной техники. Серия 15. Композиционные неметаллические материалы в машиностроении. — М.: НТЦ «Информтехника». — 2002. — Вып. 1(129). — С.5–14.
