На современном этапе одна из основных целей модернизации образования состоит в повышении его качества. Важным условием ее достижения является фундаментализация образования, предполагающая овладение соответствующими «базисными» знаниями, навыками и умениями. Первичные теоретические представления об основных понятиях темы студенты получают на лекционных занятиях. Трансформация теоретических знаний в способы деятельности возможна в случае включения обучаемого в деятельность по решению различных задач практического и прикладного характера. Насколько эффективно отработаны действия по введению основных понятий темы и работы с теоремами выясняется на итоговых занятиях. В связи с этим огромное значение приобретает организация повторения после изучения основных тем курса математики технического вуза. К одной из них и относится тема «Введение в математический анализ». Преподаватель может организовать повторение несколькими путями:
1. Повторение основных методов вычисления пределов; решение задач алгоритмического характера; итоговая самостоятельная работа — диагностика уровня овладения действиями, соответствующих различным этапам введения понятий «предел числовой последовательности» и «предел функции в точке».
2. Повторение основных методов вычисления пределов; заслушивание докладов, содержащих знания неалгоритмического уровня; итоговая самостоятельная работа — диагностика овладения действиями алгоритмического и неалгоритмического уровня. Если занятие построить только на докладах, то получим семинарское занятие.
Выбор формы проведения занятия осуществляет преподаватель, ориентируясь на подготовленность обучаемых. Вторую форму итогового повторения целесообразно выбирать преподавателю в случае, когда большинство студентов принадлежат к следующим трем группам обучаемых:
1. Студенты воспринимают и воспроизводят главную идею сообщения, программный материал усвоен ими в полном объеме и грамотно излагается. Четко выделяют главное в предстоящей учебно-познавательной деятельности и в соответствии с этим ставят ее цель и последовательно раскрывают ее в задачах. У этих студентов присутствуют познавательные мотивы, связанные с содержанием учебной дисциплины и процессом ее изучения. Волевые усилия проявляют во всех видах учебно-познавательной деятельности; доводят любую учебную работу до конца.
2. Студенты усваивают и грамотно излагают программный материал, но могут допускать небольшие пробелы, не искажающие содержания. У них также присутствуют познавательные мотивы, связанные с содержанием учебной дисциплины. Однако при серьезных затруднениях в процессе решения задачи такие студенты отступают. Их интенсивность работы возрастает при приближении конца семестра.
3. Мотивационный компонент развит слабо (в основном социальные мотивы). Однако волевые усилия проявляются в большинстве случаев: на занятиях по математике работают напряженно, часто проявляют стремление довести работу до конца, хотя способны выполнять частично продуктивную деятельность.
Таким образом, большинство студентов группы будут готовы к познавательной самостоятельности (1 и 2 выделенные группы), остальные же способны делать выводы (выделять главное) из услышанного (3-я группа).
При выполнении указанных выше условий целесообразно будет организовать итоговое повторение по теме «Введение в математический анализ» по второму пути: преподаватель за несколько недель до занятия выдает доклады наиболее успевающим студентам. В докладах содержатся теоретическая и практическая части. Последняя часть, включает в себя задачи неалгоритмического уровня овладения действиями различных этапов введения понятий «Предел числовой последовательности» и «Предел функции в точке». Перед занятием преподаватель консультирует обучаемых, которые делают доклады, дает указания, но решение задач осуществляется студентами самостоятельно.
После каждого сообщения необходимо сделать выводы, то есть выделить главное (указать новые способы вычисления пределов). Эту работу проводят студенты, не разрабатывающие доклады.
После проведения итогового занятия студенты должны
Знать: виды неопределенностей, основные способы вычисления пределов;
Уметь: вычислять пределы;
Иметь представление о нестандартных методах вычисления пределов.
Актуальность данной темы заключается в том, что понятие предела — основное понятие математического анализа, с помощью которого вводятся понятия производной, определенного интеграла, кратного интеграла, которые в свою очередь используются в следующих темах: теория функций нескольких переменных, дифференциальные уравнения, ряды. Таким образом, понятие предела является основополагающим для всего курса математического анализа.
После показа актуальности темы преподаватель организует работу по повторению основных способов вычисления пределов. Для этого он проводит устный счет пределов. Задания подбираются таким образом, что они обобщают и систематизируют действия по раскрытию всех изученных видов неопределенностей.
Задания 1, 2 (под цифрами 1,2) проверяют сформированность действий по раскрытию неопределенностей вида 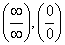 ; задание 2 (под цифрой 3) — сформированность действия по выделению существенных свойств понятия «Неопределенность
; задание 2 (под цифрой 3) — сформированность действия по выделению существенных свойств понятия «Неопределенность 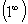 »; задание 3 (под цифрами 1, 2) — на выделение существенных свойств понятия «Первый замечательный предел»; (под цифрами 3,4) — на применение рабочей формулы второго замечательного предела.
»; задание 3 (под цифрами 1, 2) — на выделение существенных свойств понятия «Первый замечательный предел»; (под цифрами 3,4) — на применение рабочей формулы второго замечательного предела.
Задание 1. Выберите правильный ответ:
|
Ответы Условия |
0 |
|
5 |
1 |
|
1. |
||||
|
2. |
||||
|
3. |
||||
|
4. |
Задание 2. Выберите правильный ответ из числа предложенных альтернатив:
1. 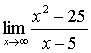
а) 5 б) 10 в) 0 г) свой ответ
2. 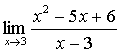
а) 1 б) -1 в) 2 г) свой ответ
3. 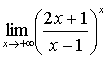
а) 2 б) 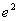 в)
в) 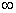 г) свой ответ
г) свой ответ
Задание 3. Заполните пропуски:
1. 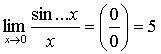
2. 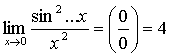
3. 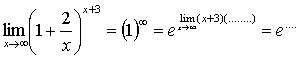
4. 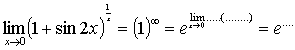
После повторения основных способов вычисления пределов заслушиваются доклады, содержащие задачи неалгоритмического уровня овладения действиями.
Например, ДОКЛАД 1.
Тема: «Предел числовой последовательности»
Теоретическая часть.
Определение: 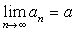 :
: 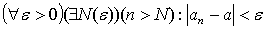
Геометрический смысл: за пределами 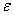 окрестности конечное число точек (N); в самой
окрестности конечное число точек (N); в самой 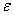 окрестности их бесконечное количество, и они «сгущаются» около точки
окрестности их бесконечное количество, и они «сгущаются» около точки 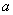 .
.
Задачи:
1) 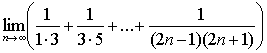
Указания: 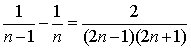
2) 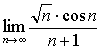
Указания: последовательность 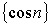 ограничена
ограничена
Всего три доклада по темам:
1. Предел функции в точке;
2. Первый замечательный предел;
3. Второй замечательный предел.
Тем самым организуется работа не только по повторению основных способов вычисления пределов, но и решаются задачи неалгоритмического содержания, т. е. преподаватель создает условия для развития познавательной самостоятельности каждого студента группы.
Проверка сформированности действий алгоритмического (1 и 2 задачи) и неалгоритмического уровня (3 задача) осуществляется посредством самостоятельной работы по вариантам.
Например, Вариант 1
1. 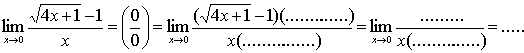
2. 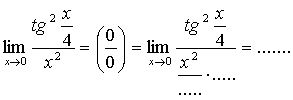
3. 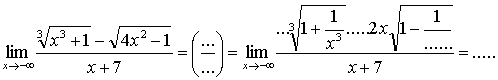
Практика показала, что использование заданий с пропусками, докладов с нестандартными задачами, способствует овладению большинством студентов знаниями не только алгоритмического уровня, но и неалгоритмического.
Литература:
1. Миганова Е. Ю. Методика конструирования систем учебных математических задач (на примере курса геометрии педвузов). Учебное пособие. — АГПИ: Саранск — Арзамас — 2001. — 96с.
2. Новичкова Т. Ю. Теория и методика использования тестов в обучении математике учащихся общеобразовательных учреждений. Дис. канд. пед наук — Пенза — 2004. — 177с.
3. Саранцев Г. И. Методическая подготовка студентов математических специальностей педагогических вузов и университетов в современных условиях: монография — Поволжское отд-ние Российской акад. образования Мордоский гос.пед. ин-т им. М. Е. Евсевьева — Саранск — 2010. — 127с.
4. Ячинова С. Н. Цели обучения как средство управления учебной деятельностью на уроке математики. Дис. канд. пед наук — Пенза — 2003. — 165с.