На начальном этапе обучения в любом техническом высшем учебном заведении бакалавры и магистры получают фундаментальную подготовку, которая играет существенную роль в их дальнейшем профессиональном образовании. Глубокое изучение фундаментальных дисциплин позволяет создать прочную базу для подготовки специалиста, способного ориентироваться в непрерывно меняющейся производственной обстановке. В связи с этим остро встает вопрос усиления фундаментальной подготовки бакалавров и магистров, возникает необходимость в создании такой системы обучения, которая способствовала бы развитию теоретического и творческого мышления, формированию умений и навыков по ориентированию в стремительно растущем потоке научной информации.
Отметим, что преподавание математики в техническом вузе должно отличаться от преподавания того же материала, например в педагогическом вузе. Дело в том, что для будущего инженера существенную роль могут играть разные вычислительные процессы, умение дифференцировать и интегрировать более или менее сложные выражения, умение найти точное или приближенное решение дифференциального уравнения. Всевозможные тонкости, связанные с обоснованиями тонких выводов, вряд ли будут играть сколько-нибудь решающую роль в практике рядового инженера, для которого важнее всего понимать существо дела.
Решая эти вопросы надо не забывать и о том, что вузовское обучение — это прежде всего обучение профессиональное. Конечно, любой из разделов математики полезен учащемуся, но невозможно включить в программу “все нужное”. Поэтому, желая усовершенствовать преподавание всегда необходимо ставить вопрос: “А нет ли более важного, более необходимого раздела для будущего специалиста, чем этот”. И только самое важное должно войти в преподавание, т. е. то, что необходимо студенту как в процессе всего обучения в вузе, так и в дальнейшей профессиональной деятельности. Таким образом, курс должен содержать то, что учащийся в отведенное время может усвоить и запомнить.
Несомненно и то, что важнейшим фактором успеха в обучении является интерес студента к науке а, следовательно, и лекция, и практические занятия должны быть интересными. Хорошо известно, что интересный материал усваивается почти без усилий и легче запоминается. Интерес к делу способен повысить и уровень логического мышления, позволяя решать задачи и усваивать материал повышенной трудности.
Что касается наших учебных программ, то они обычно просто систематически излагают курс и не обеспечивают интересного преподавания. Преподаватель должен агитировать за него, заинтересовать им, показывая силу его методов, задачи, которые он решает. Это значит, что при составлении учебных программ, подготовке лекций и практических занятий авторы должны позаботиться о подборке материала, его расположении, о подходах и постановке вопросов для того, чтобы обучающиеся были увлечены предметом. Таким образом, интерес студентов к обучению надо рассматривать как один из самых мощных стимулов обучения, а утверждение, что “преподавание должно быть интересным”, надо считать одним из важнейших положений, быть может — принципом методики.
Целесообразно также, чтобы всякая новая проблема излагалась бы как своего рода задача, поставленная перед студентами. Именно в этом случае студент будет с интересом следить за ее решением. Многое зависит и от того, как поставлен даже очевидный вопрос, как вовлечены все студенты в обсуждение поставленной проблемы.
Существенную роль в формировании профессионализма будущих специалистов может сыграть регионализация образования. Наиболее эффективными условиями для использования регионального компонента в процессе обучения можно рассматривать преподавание математических дисциплин. В частности, математика предоставляет широкие возможности для введения и обсуждения тем региональной направленности.
Регионализация образования на примере математических дисциплин может осуществляться в виде: знакомства с информационными статистическими базами вуза, Интернета, СМИ; проведения лекций, семинаров, практикумов с использованием информационных статистических данных по региону; привлечения студентов к исследовательской работе с использованием математических методов по решению вопросов и проблем региона; включения студентов в исследовательскую работу с использованием математических методов по решению вопросов экономики [1].
Использование статистических данных по региону во время учебных занятий, ресурсных информационных базы интернета, электронных СМИ способствует развитию экономического мышления и критического отношения к информации. Приведем исследования студентов ПГУАС по прогнозированию экономических показателей с помощью временных рядов на примере Пензенской области [2, 3, 4].
В качестве математических методов прогнозирования выделим методы экстраполяции, которые отличаются простотой, наглядностью и легко реализуются на ЭВМ. Методологическая предпосылка экстраполяции состоит в признании преимущественной связи между прошлым, настоящим и будущим. При этом развитие экономических явлений наиболее полно находит свое отражение во временных рядах, которые представляют собой упорядоченные во времени наборы измерений каких-либо характеристик исследуемого объекта, процесса.
В настоящее время разработана большая группа экстраполяционных методов прогнозирования отдельных экономических показателей. Наиболее распространенными методами оценки параметров аппроксимирующих зависимостей являются метод наименьших квадратов (МНК) и его модификации, метод экспоненциального сглаживания, метод вероятностного моделирования, метод адаптивного сглаживания.
Метод наименьших квадратов состоит в определении параметров модели тренда, минимизирующих ее отклонение от точек исходного временного ряда:
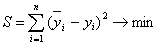
где  — расчетные (теоретические) значения исходного ряда;
— расчетные (теоретические) значения исходного ряда;
уi — фактические значения исходного ряда.
Рассмотрим практические стороны построения точечных и интервальных прогнозов на основе анализа временных рядов на примере ежеквартальных данных с 2007 года по настоящее время о стоимости газа в многоквартирных домах города Пензы.
Для получения прогноза о стоимости газа по представленным данным необходимо построить модель временного ряда. Анализ временного ряда, необходимо начинать с построения и изучения его диаграммы (рис. 1).
Визуальный анализ диаграммы данного ряда позволяет уверенно сказать, что временной ряд имеет тенденцию и не имеет сезонных и циклических компонент. Предположим, что характер тренда линейный. Определим модель тренда методом наименьших квадратов как
y(t)=a+bt.
Полученная модель тренда
y(t)=17,64+1,27t
имеет очень высокие показатели адекватности: коэффициент детерминации R2=0,917, таким образом, полученная модель на 92 % объясняет изменение стоимости; уровень значимости F-критерия составляет 6,84E-08, что существенно меньше 0,01, т. е. полученная модель является высоко значимой; уровень значимости t-критерия составляет 2,55E-10, что существенно меньше 0,01, следовательно, все коэффициенты статически значимы.
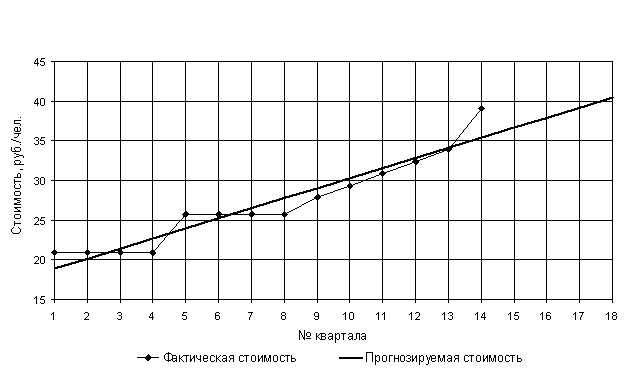
Рис. 1. Стоимость газа по г.Пензе
В целом можно сделать вывод, что полученная модель тренда достаточно адекватно описывает исследуемую статистическую зависимость и вполне пригодна для получения обоснованных заключений и прогнозов.
Экономическая интерпретация модели позволяет сделать вывод о том, что цена на газ в г. Пенза за квартал дорожает в среднем на 1 рубль 27 копеек.
Рассчитаем точечные прогнозы для значений стоимости газа на начало 2014 года (руб.):
1 кв. 2014г.: y17=17,64+1,27*17=39,21
2 кв. 2014г.: y18=17,64+1,27*18=40,48
Рассмотрим процесс получения интервальных прогнозов по формуле


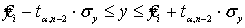 ,
,
где  - точечный прогноз;
- точечный прогноз;
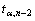 -критическое значение t- критерия при уровне значимости α и числе степеней свободы m=n-2 (t0,05;12= 2,2);
-критическое значение t- критерия при уровне значимости α и числе степеней свободы m=n-2 (t0,05;12= 2,2);
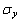 -ошибка прогноза.
-ошибка прогноза.
Ошибку прогноза определяется по формуле:
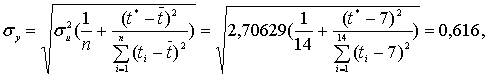
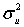 - дисперсия отклонений;
- дисперсия отклонений;
t*- порядковый номер периода времени, на который рассчитывается прогноз.
Очевидно, что использование полученной модели тренда для среднесрочного и тем более долгосрочного прогнозирования недопустимо.
Таким образом, процесс использования региональной статистической, цифровой информации в единстве с изучаемой дисциплиной способствуют осознанному восприятию теории и закладывает основы для формирования творчески активных, неравнодушных специалистов. Изложение материала, связывающее его с практикой — один из приемов, способствующий возбуждению интереса у студентов. Если учащийся видит, что наука возникла в результате определенных потребностей общества, и содействует ему в решении профессиональных задач, то это уже пробуждает интерес к делу. Тогда и те теоретические тонкости, которые часто так трудно преодолевать в сухом формальном изложении, здесь будут усваиваться значительно легче, так как учащийся будет чувствовать себя заинтересованным в их преодолении и будет понимать, почему они возникают.
Литература:
1. Корощенко Н. Л. Региональный компонент содержания образования математических дисциплин как фактор формирования профессионализма будущих специалистов [Текст]/ Н. Л. Корощенко// Проблемы преподавания математики в школе и вузе в условиях реализации новых образовательных стандартов: Сборник научных статей. — Тобольск: ТГСПА им. Д. И. Менделеева, 2012.
2. Круглов Ю. В. Исследование и статистическое моделирование расселения населения [Текст]/ Ю. В. Круглов, Е. С. Стецурина, О. В. Снежкина // Вестник Сибирской государственной автомобильно-дорожной академии. 2013. № 2 (30). С. 62–67.
3. Снежкина О. В. Прогнозирование экономических показателей с помощью временных рядов [Текст]/ О. В. Снежкина, Г. А. Левова// Материали за 9-а международна научна практична конференция, «Новини на научния прогрес», — 2013. Том 1. Икономики. София. «БялГРАД-БГ» ООД
4. Кубис В. А. Моделирование эффективности работы защитной газовоздушной завесы [Текст]/ В. А. Кубис, С. А. Степанов, О. В. Снежкина, А. П. Левцев // Региональная архитектура и строительство. 2012. № 1(12)







