Рассматривается программная модель для исследования траектории движения транспортного робота по трассе, заданной опорными точками с использованием различных алгоритмов управления. Модель используется в учебном процессе.
Введение
Робототехника внесла существенный вклад в повышение производительности и качества, однако ввод в эксплуатацию роботизированной ячейки, а так же обучение высококвалифицированных специалистов (в том числе и студентов) в условиях реального производства может оказаться весьма затратным с точки зрения финансов и времени.
Проектирование методического и материально-технического обеспечения лабораторных циклов по учебным дисциплинам связано с преодолением достаточно противоречивых ограничений, среди которых наиболее существенными представляются:
- создание дидактических средств для приобретения навыков работы с исследуемыми объектами;
- гибкость комплектования лабораторных установок объектами исследования;
- обеспечение мер безаварийной эксплуатации исследуемых объектов в процессе выполнения работы и при непреднамеренных нарушениях режимов;
- стоимость обеспечения лабораторного цикла;
- возможность тиражирования и поставки средств обеспечения лабораторных циклов потребителям.
Наличие программной интегрированной обучающей среды с набором виртуальных моделей различных технологических объектов и с удобным пользовательским интерфейсом позволяет самостоятельно осваивать изучаемую дисциплину, контролировать уровень знаний студентов, выполнять практические и лабораторные работы
Постановка задачи моделирования движения робота
Необходимо создать программную модель для исследования различных законов управления транспортным роботом по траектории, заданной опорными точками при наличии внешних помех. Робот движется в плоскости в декартовой системе координат. Движение происходит из некоторой начальной точки в заданную конечную точку по нелинейной траектории с заданной курсовой скоростью Vk. В начальный и конечный момент времени скорость движения равна нулю. Наброс скорости (изменение скорости за один цикл управления) постоянен и составляет ΔV. Управление производится по двум ортогональным приводам.
Режимы работы модели: ручной/ автоматический.
В ручном режимемогут задаваться:
- опорные точки траектории,
- курсовая скорость,
- наброс скорости,
- условия остановки движения.
Возможные состояния в автоматическом режиме:
- пуск,
- останов,
- сброс.
Модель для исследования движения робота
Релейный закон управления. В системах, где инерционность объекта не играет существенной роли и не требуется точного выхода в заданную точку, может использоваться релейный способ управления, т. к. он технически легко реализуется:
VX = sign(Xi-Xt)*VK (1)
Vp = sign(Yi-Yt)*Vk,
где Хi, Yi — координаты очередной опорной точки,
Хt, Yt — текущие координаты,
Vx, Vy — компоненты вектора курсовой скорости.
При релейном законе управления величина скорости по обеим осям одинакова и равна VK. Это приводит к тому, что невозможно организовать движение точно по заданной траектории (контурное управление), но легко реализуется выход в заданную точку (позиционное управление).
Данный алгоритм имеет существенные недостатки:
- скорость движения никогда не обращается в нуль,
- скорость изменяется мгновенно при переходе через заданную точку, что в реальных условиях выполнить невозможно.
Рассмотрим простой вариант формирования вектора скорости инерционного объекта, ориентированный на релейный закон. Инерционность в модели будет задаваться набросом скорости ΔV. Увеличенный наброс, при управлении будет, с одной стороны, уменьшать время разгона и торможения, а с другой — может повысить неустойчивость системы управления.
Используем вспомогательные переменные:
Vpx:=sign(X3-Xt)*Vk;
Vpy:=sign(Yi-Yt)*Vk;
Если модуль реальной скорости по соответствующей координате меньше заданной, то объект разгоняется с набросом скорости ΔV:
abs (Vx)<=abs(Vpx) then Vx:=Vx+ΔV*sign(Xi-Xt) (2)
иначе скорость равна заданной:
Vx:=Vk*sign(Хi-Xt).
И аналогично, если
abs(Vy)<=abs(Vpy) then Vy:=Vy+ΔV*sign(Yi-Yt)
иначе
Vy:=Vk*sign(Yi-Yt).
Управление движением по нелинейной траектории. Для определения направления движения по заданной нелинейной траектории необходимо рассчитать компоненты вектора курсовой скорости Vx и Vy по формулам для вычисления:
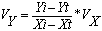
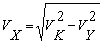 (3)
(3)
где Vk — заданная курсовая скорость.
Разрешая данную систему уравнений относительно Vx и Vy, можно задать на модели скорость движения по траектории безинерционного объекта.
Управление инерционным объектом. В рассмотренном алгоритме нужно уделить внимание изменению Vx и Vy с учетом наброса скорости в начальной точке (X0, Y0), в конечной (Хк, Ук) и в промежуточных опорных точках (Xi, Yi). Решение данных уравнений позволяет управлять роботом с необходимой точностью, однако такие формулы не практичны при дефиците времени, так как машина долго выполняет такие операции, как нахождение квадратного корня, умножения и деления.
Приближенный метод расчета вектора скорости. Предлагаются так же различные приближенные способы расчета VX и VY по заданной VK, исключающие использование “долгих” команд.
Предположим, что VX — независимая компонента (const), например
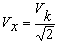
Тогда
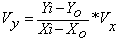
При равенстве компонент VX и VY модуль вектора реальной скорости составит
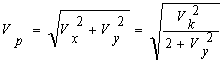
При изменении координат Xi, Yi компонента Vx будет оставаться постоянной, а вектор скорости Vy будет очень быстро и сильно расти, следовательно, реальная скорость будет очень велика. Поэтому этот алгоритм модифицируем.
Добавим следующие условия:
Если |Xi — Xt| < |Yi — Yt|, то
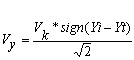 и
и 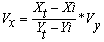
иначе
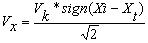 и
и 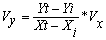
Режим торможения в дискретной системе управления имеет свои нюансы. Для исключения перерегулирования необходимо вычислять и учитывать тормозной путь для текущей скорости:
Sx = Vx2 / 2ΔVиSy = Vy2 / 2ΔV
Остановить робот мгновенно и точно в заданной точке невозможно (что связано, в частности, с особенностями представления информации в дискретной форме), поэтому приходится вводить параметр ε, — точность выхода в заданную точку. Определим ∆X и ∆Yпри движении к очередной (или конечной) точке:
∆X= Xt — Xiи ∆Y= Yt — Yi
В соответствии с этим смену опорной точки (или торможение) следует производить в некоторой окрестности ε, радиус которой будет зависеть от требуемой точности навигации: ∆X2 + ∆Y2 ≤ ε 2.
Модель для исследования движения робота
Интерфейс компьютерной модели (рис. 1) представлен в виде графической сетки в декартовых координатах, окон для ввода параметров управления и задания опорных то чек, информационных окон для вывода формул закона управления и вывода текущих координат при движении по траектории, кнопок управления моделью.
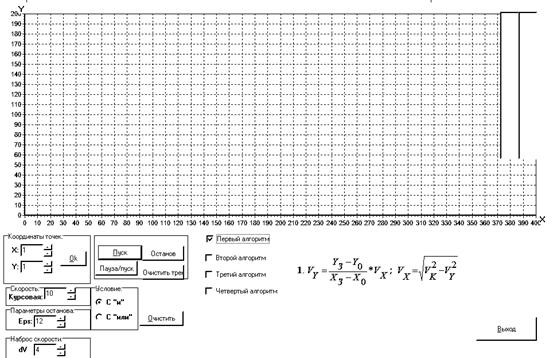
Рис. 1. Интерфейс программы «Транспортный робот»
Модель позволяет задать траекторию движения робота, наброс скорости, курсовую скорость перемещения (как на этапе инициализации движения, так и во время перемещения) и задать условия останова. Останов, или смена опорной точки может происходить если обе текущие координаты (условие И) попали заданную окрестность, или хотя бы одна из них (условие ИЛИ).
На рис. 2. представлена траектория движения безинерционного объекта при релейном управлении в соответствии с формулой (1). Траектория задана двумя точками: начальной и конечной, т. е. движение должно происходить по прямой, соединяющие эти точки, причем скорость в начале и в конце V(t=0)=0 и V(t=Tk)=0. При равенстве модулей скорости Vx и Vy движение происходит с курсовым углом в ±45о. Изменение вектора скорости происходит мгновенно.
При использовании релейного закона (см. формулу (2)) для инерционного объекта (рис. 3) траектория движения сглаживается, но на стационарных участках движение, опять же, происходит с курсовым углом в ±45о.
Изменение наброса скорости влияет на качество управления. С уменьшением наброса скорости уменьшается скорость движения робота, следовательно, транспортный робот точнее выйдет в заданную точку. При увеличении наброса скорости наблюдается перерегулирование (неустойчивое состояние объекта, не происходит остановки движения). На этих примерах видно, что релейный закон имеет смысл использовать при позиционном управлении. Для контурного управления этот закон иногда используют, но при этом заданную непрерывную траекторию аппроксимируют ступенчатой траекторией.

Рис. 2. Релейный закон управления, безынерционный объект
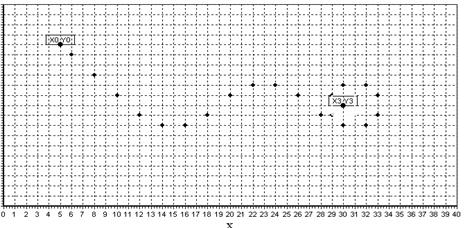
Рис. 3. Релейный закон управления, инерционный объект
На рис. 4 представлена траектория движения инерционного объекта при контурном управлении в соответствии с формулами (3). Хорошо видно, что в начале траектории объект наращивает курсовую скорость, затем переходит в стационарный режим движения и в близи конечной точки начинается торможение. Но за счет инерции происходит переход через конечную точку. Поскольку компоненты скорости различны:
|Vx| > |Vy|
перерегулирование по координате Х много больше, чем по координате Y.
На компьютерной модели можно количественно и качественно исследовать для различных законов управления, различных заданных траекторий, различных параметров системы управления:
- вид реальной траектории движения,
- погрешности удержания объекта на заданной траектории,
- влияние пространственной крутизны траектории на качество управления,
- время прохождения траектории,
- влияние таких параметров, как наброс скорости, значение курсовой скорости, размер заданной окрестности при смене опорной точки или останова.
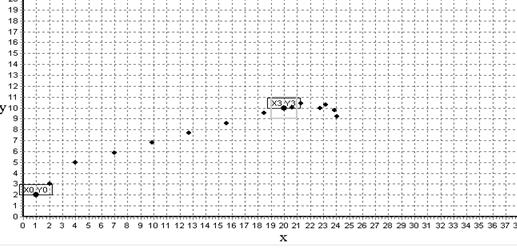
Рис. 4. Траектория инерционного объекта при контурном управлении
Заключение
Разработана программная модель транспортного робота, движущегося по заданной траектории для лабораторной работы по дисциплине «Моделирование робототехнических систем». Проведен качественный анализ двух законов управления транспортным роботом: релейным законом и релейным инерционным законом.
Литература:
2. Раводин О. М. Бейнарович В. А. Принципы построения программного обеспечения копировально-фрезерных станков Аппаратно-программные средства автоматизации технологических процессов. -Изд-во ТУСУР, Томск 1998.
3. Раводин О. М. Гибкие производственные системы и робототехника. Учебное пособие. Издание 2-ое переработанное и дополненное. — Томск: В-Спектр, 2007. — 260 с.







