В статье изложена инженерная методика для расчета параметров суспензии в выпарных аппаратах. Рассматриваются растворы при концентрациях, достигших предельные значений, в результате чего происходит образование твердой фазы. Расчетная область представляет собой U‑образный сосуд, в нисходящей ветви которого параметры известны, а в восходящей ветви находится суспензия — смесь насыщенного раствора соли и взвешенных частиц твердой фазы. Учтено положение уровня в восходящей ветви, оказывающее влияние на массу раствора и твердой фазы. Методика пригодна для инженерных оценокпри конструкторских разработках.
Ключевые слова: раствор, фаза, концентрация, баланс, масса, динамика, перепад уровней.
В химических технологиях широко применяются выпарные аппараты. Основные процессы в них описаны в классических трудах [1, 2]. Автором рассматривались близкие по тематике задачи — изменение концентрации без фазовых переходов, а также образование твердой фазы на стенках [3, 4]. Вне поля внимания остались задачи по определению параметров двухфазной смеси — суспензии. Особую актуальность данные процессы получают в случае резкого изменения температуры жидкой фазы при условии, что достигаются предельные значения растворимости солей. Это может происходить, например, при аварийных режимах в выпарных аппаратах и прочих устройствах.
Пусть расчетный объект представляет собой два сообщающихся сосуда (см. Рис. 1). Перетоки жидкой среды между сосудами могут осуществляться через канал вблизи дна. В первом сосуде, «опускной» участок, пусть находится среда с известными определяющими параметрами (плотность, уровень), которые необходимы для вычисления параметров весового столба в нем. Во втором сосуде, «подъемный» участок, находится суспензия.
Задача расчета следующая. Необходима проверка возможности существования, а затем — уточнение параметров состояния суспензии в подъемном участке. Этому предшествует запись балансовых соотношений для массы соли в подъемном участке:
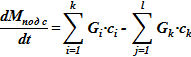
Для конкретного момента времени необходимо вычислить значение суммарной массы соли, находящейся в виде смеси насыщенного раствора и твердой фазы в подъемном участке —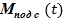 
.
Полученное значение является основным при построении решения, в котором уже будут конкретизироваться параметры состояния суспензии — солевой раствор при предельной концентрации и равномерно распределенные в нем твердые частицы соли.
Расчету параметров суспензии в «подъемном» участке предшествуют оценки правомерности поиска решения для смеси в виде суспензии. С этой целью производится вычисление параметров среды в «подъемном» участке для двух предельных вариантов решения: 1) максимальный уровень среды hmaxпод, когда имеем исключительно солевой раствор при предельной концентрации без твердой фазы; 2) минимальный уровень среды hmin под, когда имеем исключительно твердую фазу — кристаллы. Полученные значения используются для проверки наличия решения и обоснования правомерности использования алгоритма.
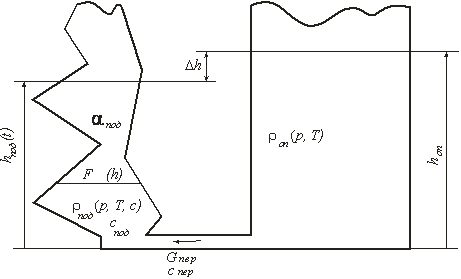
Рис. 1. Схема расчетной области
Исходные данные для расчета:
- зависимость площади поперечного сечения в подъемном участке от высоты,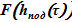 
;
- плотности жидкой и твердой фазы для подъемного участка — ρпод ж (плотность раствора жидкости при предельной растворимости), ρпод к;
- плотность среды и уровень в опускном участке ρоп и hоп;
- концентрация cпод ж, г/кг для раствора в подъемном участке. Данная величина при рассмотрении суспензии равна предельной концентрации;
- суммарное количество соли в подъемном участке Mпод с, находящейся в жидкой (раствор) и твердой (кристалл) фазе. Как упоминалось выше, эта величина определяется из балансовых соотношений с привлечением граничных условий — расходов подачи/отбора среды. Для сокращения выкладок принято, что твердая фаза — кристаллы,- формируется исключительно из соли.
Основные используемые соотношения при построении алгоритма:
1) Равенство весовых столбов в опускном и подъемном участке
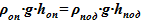
2) Зависимость объема в подъемном участке от физического уровня смеси
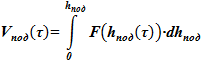
3) Зависимость плотности и удельного объема суспензии от объемного и массового содержание твердой фазы
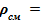ρж + α· (ρк — ρж),
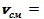vж — х· (vж — vк)
Алгоритм расчета параметров суспензии следующий. Нужно определить верхнюю, максимально возможную оценку для массы соли, а также минимально возможную оценку для массы соли в суспензии. Если искомое значение массы соли лежит в указанной области, то можно отыскать решение с помощью итеративных вычислений.
1) Определяется максимально возможный уровень выродившейся суспензии, когда без содержания твердой фазы (α=0) и основные параметры для этого случая
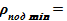ρпод ж + α· (ρпод к — ρпод ж) = ρпод ж,
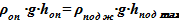
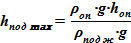
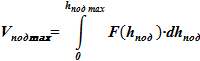
Mпод с min = Vпод max· ρпод ж · cпод ж /1000
2) Определяется минимально возможный уровень выродившейся суспензии, когда объемное содержание твердой фазы равно α=1
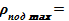ρпод ж + α ·(ρпод к — ρпод ж) = ρпод к
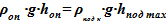
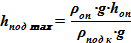
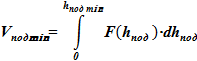
Mпод с max = Vпод min· ρпод к
3) Проверяется возможность существования решения для двухфазной смеси — суспензии
Mпод с min £Mпод с £ Mпод с max
и, если неравенство соблюдается, производится переход к итеративному процессу поиска решения
4) Принимаем новое значение уровня в подъемном участке и определяемые им величины для двухфазной смеси — плотность, объем
hпод н = (hпод max + hпод min) · 0,5
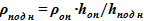; vпод н = 1/ρпод н
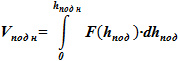
5) Вычисляем объемное и массовое содержание твердой фазы
xпод н = 1-((vпод н — vпод к)/(vпод ж — vпод к))
αпод н = 1-((ρпод н — ρпод ж)/(ρпод к — ρпод ж))
6) В этом случае можно определить значения объемов и масс для каждого из компонентов смеси при заданном уровне смеси в подъемом участке hпод н
Vпод н к = Vпод н · αпод н;Vпод н ж=Vпод н-Vпод н к
Mпод н к = Vпод н к · ρпод к;Mпод н ж=Vпод н ж · ρпод ж,
7) Вычисляется масса соли, находящейся в растворе, и суммарная масса соли в обоих фазовых состояниях — жидком и твердом
Mпод н ж с= Mпод н ж спод ж/1000; Mпод н с = Mпод н ж с + Mпод н к
8) Проводится сравнение вычисленного значения суммарной массы соли в обеих фазах с заданным в граничных условиях. Если точность решения не удовлетворительная, то происходит изменение предельных значений для высоты смеси в подъемном участке и повторяется итеративный процесс, начиная с пункта 4)
hпод max = hпод н, еслиMпод с ≥ Mпод н с
или
hпод min = hпод н, еслиMпод с £ Mпод н с
Данная методика проста и может применяться для описания различных процессов, в которых появляется необходимость поиска параметров двухфазной смеси — суспензии. Детальное описание, построение моделей с дополнительными параметрами и учет процессов, оставшихся вне поля зрения, — это следующий шаг, который должен рассматриваться в дальнейшем.
Список условных обозначений:
M — масса, кг;
h — высота, м;
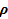— плотность, кг/м3;
G — расход, кг/с;
с — концентрация, г/кг;
V — объем, м3;
α (х) — объемное (массовое) содержание твердой фазы в суспензии.
Литература:
1. Касаткин А. Г. Основные процессы и аппараты химической технологии. М.: Химия, 1971, 784 с.
2. Гельперин Н. И. Основные процессы и аппараты химической технологии. М.: Химия, 1981, 812 с.
3. Шмаль И. И. Аналитические оценки для процесса кристаллизации // Молодой ученый. — 2013. — № 7 (54), с. 30–31.
4. Шмаль И. И. Метод расчета нестационарных изменений концентрации в выпарных установках // Молодой ученый. — 2013. — № 8 (55), с. 42–44.
