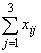Ограничимся тремя основными задачами статистического анализа связей между ранжировками в маркетинговых исследованиях.
Анализ структуры совокупности упорядочений. Если точки xk разбросаны равномерно по всей области их возможных значений 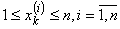 , то связь (согласованность) между ранжировками Xk = (xk(1), xk(2),..., xk(n))т, практически отсутствует.Если имеется ядро (сгусток близко лежащих друг от друга точек), то имеется согласованность переменных.При наличии нескольких ядер можно говорить о наличии нескольких подмножеств переменных с высокой степенью взаимосвязей между входящими в ядра переменными.
, то связь (согласованность) между ранжировками Xk = (xk(1), xk(2),..., xk(n))т, практически отсутствует.Если имеется ядро (сгусток близко лежащих друг от друга точек), то имеется согласованность переменных.При наличии нескольких ядер можно говорить о наличии нескольких подмножеств переменных с высокой степенью взаимосвязей между входящими в ядра переменными.
Анализ интегральной (совокупной) согласованности переменных и их условная ранжировка по критерию степени тесноты связи каждой из них с остальными переменными. Такая задача возникает при определении степени согласованности мнений экспертов, и условном упорядочении экспертов по их компетентности. В основе анализа лежит определение коэффициента совокупной согласованности — коэффициента конкордациидля различных комбинаций переменных.
Регрессия на порядковых (ординальных) переменных. Здесь осуществляется наилучшее (в определённом смысле) восстановление ранжировки
Xo = (xo(1), xo(2),..., xo(n))т, связанной с результирующей переменной 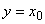 , по ранжировкам X1,X2,..., Xp (соответствуют объясняющим переменным x1, x2,..., xp).
, по ранжировкам X1,X2,..., Xp (соответствуют объясняющим переменным x1, x2,..., xp).
Ранжирование признаков. При решении этих задачиспользуется установленная между двумя качественными признаками изделия связь, когда каждый из этих признаков допускает лишь относительное сравнение различных изделий («лучше» — «хуже») без указания численных значений признаков [1,2]. Если выборка изделий O(i), 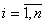 , сравнивается по каждому из p + 1 признаков
, сравнивается по каждому из p + 1 признаков 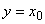 ; x1,x2,..., xp (порядковых переменных), то результатом измерения каждой из порядковых переменных является приписывание каждому из обследованных объектов некоторой условной числовой метки, обозначающей место объекта в ряду из всех n анализируемых объектов (упорядочение по убыванию степени проявления в них k-го, , изучаемого свойства). Число xk(i), определяющее место O(i) по k-му признаку, и будет рангом i-го объекта по k-мупризнаку(табл. 1).
; x1,x2,..., xp (порядковых переменных), то результатом измерения каждой из порядковых переменных является приписывание каждому из обследованных объектов некоторой условной числовой метки, обозначающей место объекта в ряду из всех n анализируемых объектов (упорядочение по убыванию степени проявления в них k-го, , изучаемого свойства). Число xk(i), определяющее место O(i) по k-му признаку, и будет рангом i-го объекта по k-мупризнаку(табл. 1).
Таблица 1
|
Порядковый номер объекта |
Порядковый номер исследуемой переменной (свойства) |
||||||
|
0 |
1 |
2 |
... |
k |
... |
p |
|
|
1 |
xo(1) = y(1) |
x1(1) |
x2(1) |
... |
xk(1) |
... |
xp(1) |
|
2 |
xo(2) = y(2) |
x1(2) |
x2(2) |
... |
xk(2) |
... |
xp(2) |
|
|
... |
... |
|||||
|
i |
xo(i) = y(i) |
x1(i) |
x2(i) |
... |
xk(i) |
... |
xp(i) |
|
|
... |
... |
|||||
|
n |
xo(n) = y(n) |
x1(n) |
x2(n) |
... |
xk(n) |
... |
xp(n) |
Столбец с номером k, , указанной таблицы представляет собой перестановку из n натуральных чисел 1, 2,..., n, определяющую порядковые места объектов O(1),O(2),..., O(n) вряду, упорядоченном по свойству xk.
Неполные последовательности рангов. При маркетинговых исследованиях часто используются так называемые неполные последовательности рангов. Приведем задачу определения стратегии предприятия, выпускающего цемент семи сортов с учётом предпочтения покупателей, а также исходя из упорядочений суждений нескольких покупателей. Предполагается, что предприятием при предварительной оценке покупателям предоставляются не все сорта цемента (например, с целью экономии времени и средств). Каждый сорт цемента оценивается одинаковое число раз, а каждая пара — по одному разу. Таким образом, все элементы сопоставляются одинаковое число раз (табл.2). В каждой последовательности отсутствуют оценки 4-х сортов.
Таблица 2
|
Покупатели |
Сорт цемента |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
+ |
+ |
+ |
||||
|
2 |
+ |
+ |
+ |
||||
|
3 |
+ |
+ |
+ |
||||
|
4 |
+ |
+ |
+ |
||||
|
5 |
+ |
+ |
+ |
||||
|
6 |
+ |
+ |
+ |
||||
|
7 |
+ |
+ |
+ |
||||
Оценки покупателей приведены в табл.3.
Таблица 3
|
Покупатели |
Сорт цемента |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
2 |
1 |
3 |
||||
|
2 |
2 |
3 |
1 |
||||
|
3 |
1 |
2 |
3 |
||||
|
4 |
1 |
3 |
2 |
||||
|
5 |
1 |
2 |
3 |
||||
|
6 |
1 |
2 |
3 |
||||
|
7 |
1 |
2 |
3 |
||||
|
|
4 |
4 |
6 |
6 |
6 |
8 |
8 |
Согласованность мнений покупателей оценивалась по коэффициенту конкордации:
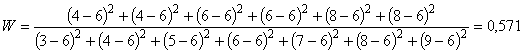 .
.
Если из общего числа n объектов в эксперименте каждый раз содержится k объектов и каждый из них участвует в эксперименте в общей сложности m раз, то всего будет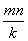 групп. При этом в каждой группе будет сопоставляться между собой
групп. При этом в каждой группе будет сопоставляться между собой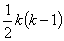 пар; общее число сопоставлений равно
пар; общее число сопоставлений равно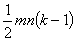 ; общее число групп, в которых встречается заданная пара элементов
; общее число групп, в которых встречается заданная пара элементов 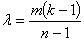 (l — целое число; m (k — 1) должно делиться на (n — 1) без остатка;
(l — целое число; m (k — 1) должно делиться на (n — 1) без остатка; 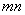 дoлжно делиться на k без остатка; эти условия накладывают ограничения на числа, используемые при составлении такого рода планов экспериментов). В рассмотренном примере n = 7, k = 3 (m должно делиться на 3). При этом l= 1. В общем случае
дoлжно делиться на k без остатка; эти условия накладывают ограничения на числа, используемые при составлении такого рода планов экспериментов). В рассмотренном примере n = 7, k = 3 (m должно делиться на 3). При этом l= 1. В общем случае 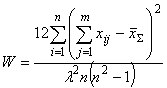 (для рассмотренного примера
(для рассмотренного примера 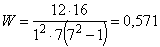 ).
).
Диаграммы предпочтений. Рассмотрим на конкретном примере. Эксплуатирующей организации поочерёдно предлагались по два из 6 видов теплоизоляционного материала (всего 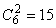 пар). Каждый раз фиксировалось, какой материал потребителем используется в первую очередь (табл.4).
пар). Каждый раз фиксировалось, какой материал потребителем используется в первую очередь (табл.4).
Таблица 4
|
Вид материала |
Вид материала |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
- |
1 |
1 |
0 |
1 |
1 |
|
2 |
0 |
- |
0 |
1 |
1 |
0 |
|
3 |
0 |
1 |
- |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
- |
0 |
0 |
|
5 |
0 |
0 |
0 |
1 |
- |
1 |
|
6 |
0 |
1 |
0 |
1 |
0 |
- |
Запись 1 в клетке, находящейся на пересечении столбца 2 и строки 1, означает, что материал 1 предпочтительнее 2, а запись 0 в клетке, находящейся на пересечении столбца 4 и строки 1, означает, что материал 4 предпочтительнее материала 1.
Система предпочтений оценивалась по диаграмме (объекты от 1 до 6 располагаются по вершинам правильного многоугольника; если 1 предпочтительнее 2, то стрелка направлена от 1 к 2 вдоль линии 1–2 (рис. 1).).
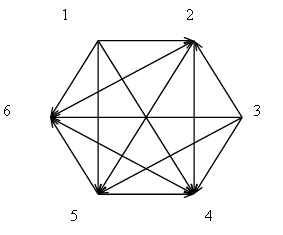
Рис.1
Здесь всего 5 циклов предпочтения по трём объектам:
1 ® 2 ® 4 ® 1
1 ® 3 ® 4 ® 1
2 ® 5 ® 6 ® 2
1 ® 6 ® 4 ® 1
1 ® 5 ® 4 ® 1
(5 несовместимыхситуаций; обычно, если 1 ® 2, 2 ® 4, то 1 ® 4, а здесь имеем 4 ® 1).
Коэффициент совместности: (n — нечётно); (n — чётно), 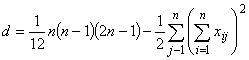 – число обнаружившихся циклов предпочтений по трём объектам;
– число обнаружившихся циклов предпочтений по трём объектам; 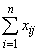 – сумма чисел по строкам.
– сумма чисел по строкам.
В рассматриваемом случае 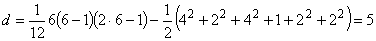 ;
;
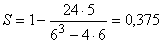 .
.
Циклы предпочтений по всем объектам отсутствуют (ранговые оценки удаётся упорядочить тогда и только тогда, когда S = 1!).
Согласованность между предпочтениями экспертов. Рассмотрим задачу определения согласованности мнений покупателей о качестве продукции на примере оценки кровельного материала. В эксперименте участвовали m покупателей (экспертов), каждый из которых рассматривал все возможные пары из n объектов и определял 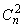 предпочтений. В таблице, аналогичной указанной выше, при x ® y вписывается 1 в клетку, расположенную на пересечении строки с номером x и столбца с номером y. Затем определяется количество единиц в каждой клетке (от 0 до m). Если эксперты единодушны, то
предпочтений. В таблице, аналогичной указанной выше, при x ® y вписывается 1 в клетку, расположенную на пересечении строки с номером x и столбца с номером y. Затем определяется количество единиц в каждой клетке (от 0 до m). Если эксперты единодушны, то 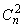 клеток будут содержать по m единиц, а в остальных — нули.Если в клетке, находящейся на пересечении строки с номером x и столбца с номером y, стоит число gi j, то
клеток будут содержать по m единиц, а в остальных — нули.Если в клетке, находящейся на пересечении строки с номером x и столбца с номером y, стоит число gi j, то 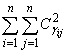 определяет общее число случаев, в которых у пары экспертов одинаковые оценки. Полная согласованность в предпочтениях экспертов достигается при коэффициенте согласия U = 1. В общем случае справедливо
определяет общее число случаев, в которых у пары экспертов одинаковые оценки. Полная согласованность в предпочтениях экспертов достигается при коэффициенте согласия U = 1. В общем случае справедливо 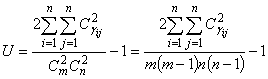 .
.
Определялись предпочтения относительно использования 5 видов кровли, высказанные 21 покупателем (табл.5).
Таблица 5
|
Вид кровли |
1 |
2 |
3 |
4 |
5 |
S |
|
1 |
- |
14 |
11 |
14 |
24 |
53 |
|
2 |
7 |
- |
14 |
13 |
15 |
49 |
|
3 |
10 |
7 |
- |
11 |
13 |
41 |
|
4 |
7 |
8 |
10 |
- |
13 |
38 |
|
5 |
7 |
6 |
8 |
8 |
- |
29 |
|
Итого: |
210 |
Здесь: 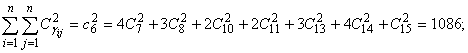
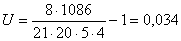
(согласованность между предпочтениями покупателей практически отсутствует).
Таким образом, при маркетинговых исследованиях формализация оценок эффективно может производиться методами ранговой корреляции. Приведенный подход также успешно использовался при выборе модификаторов для серных композитов [3], изучении флокулообразования в дисперсных системах [4], когнитивном моделировании композитов [5].
Литература:
1. Будылина Е. А., Гарькина И. А. Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. -2013. — № 2(16). -C. 138–143.
2. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. -2013. -№ 5. С. 42–45.
3. Гарькина И. А. Модификаторы для серных композитов специального назначения / Известия высших учебных заведений. Серия: Химия и химическая технология. — 2008. –Т.51. № 5. — С. 70–75.
4. Гарькина И. А., Данилов А. М., Смирнов В. А. Флокуляция в дисперсных системах/ Системы управления и информационные технологии. — 2008. — № 2.3(32). — С.344–347.
5. Гарькина И. А., Данилов А. М., Королев Е. В. Когнитивное моделирование при синтезе композиционных материалов как сложных систем / Известия ВУЗов. Строительство. — 2009. — № 3/4. — С.30–37.