Предварительно рассмотрим задачу определения аналитических зависимостей по экспериментальным данным в общей постановке. Пусть результатом измерения физической величины, находящейся при проведении всей серии измерений в неизменном состоянии, является ряд чисел 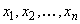 ,
, 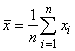 - среднее арифметическое наблюдённых значений (ошибки измерений:
- среднее арифметическое наблюдённых значений (ошибки измерений: 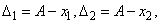 …,
…, 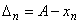 ; A- истинное значение измеряемой величины).
; A- истинное значение измеряемой величины).
Если наиболее вероятным значением искомой величины A принять 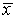 , то законом распределения случайных ошибок будет нормальный закон Гаусса с плотностью вероятностей
, то законом распределения случайных ошибок будет нормальный закон Гаусса с плотностью вероятностей
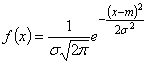 ,
,
где m — математическое ожидание;
s – среднее квадратическое отклонение случайной величины X.
В соответствии с теоремой Чебышева при достаточно большом числе независимых опытов среднее арифметическое 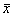 наблюдённых значений случайной величины X сходится по вероятности к её математическому ожиданию m (при бесконечно большом числе измерений истинное значение измеряемой величины A будет равно среднеарифметическому значению
наблюдённых значений случайной величины X сходится по вероятности к её математическому ожиданию m (при бесконечно большом числе измерений истинное значение измеряемой величины A будет равно среднеарифметическому значению 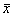 результатов всех произведённых измерений). Предполагается, систематические погрешности отсутствуют. Если измеряемая величина за время измерений меняется вследствие непостоянства другой величины, связанной с ней, то и в этих случаях будет наблюдаться статистический разброс, приводящий к случайным погрешностям (разброс будет уже проходить не относительно неизменного «истинного», или среднего значения измеряемой величины, а относительно изменяющегося «истинного значения»).
результатов всех произведённых измерений). Предполагается, систематические погрешности отсутствуют. Если измеряемая величина за время измерений меняется вследствие непостоянства другой величины, связанной с ней, то и в этих случаях будет наблюдаться статистический разброс, приводящий к случайным погрешностям (разброс будет уже проходить не относительно неизменного «истинного», или среднего значения измеряемой величины, а относительно изменяющегося «истинного значения»).
Установление эмпирической зависимости 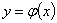 сводится к проведению по данным экспериментальным точкам некоторой кривой (не ломаной), которая проходила бы как можно ближе к истинной функциональной зависимости
сводится к проведению по данным экспериментальным точкам некоторой кривой (не ломаной), которая проходила бы как можно ближе к истинной функциональной зависимости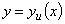 .
.
Значению аргумента 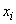 соответствует истинное значение измеряемой величины
соответствует истинное значение измеряемой величины 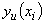 , а в результате измерения вместо
, а в результате измерения вместо 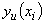 получим случайную величину
получим случайную величину 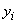 . Так как ошибки измерения величины
. Так как ошибки измерения величины 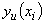 распределены по нормальному закону с математическим ожиданием, равным
распределены по нормальному закону с математическим ожиданием, равным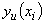 , и со средним квадратическим отклонением
, и со средним квадратическим отклонением 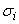 (характеризует ошибку измерения), то случайная величина будет распределена по нормальному закону:
(характеризует ошибку измерения), то случайная величина будет распределена по нормальному закону:
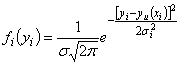 , (
, (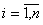 ).
).
Таким образом, в результате ряда измерений произошло следующее событие B: случайные величины (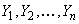 ) приняли совокупность значений
) приняли совокупность значений 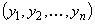 . Тогда установление эмпирической зависимости
. Тогда установление эмпирической зависимости 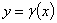 сводится к подбору математических ожиданий случайных величин
сводится к подбору математических ожиданий случайных величин 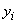 , равных
, равных 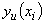 , чтобы вероятность события B была максимальна (принцип максимального правдоподобия). Оказывается, если точность измерения при всех
, чтобы вероятность события B была максимальна (принцип максимального правдоподобия). Оказывается, если точность измерения при всех 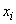 одинакова и равна s, то, для того чтобы совокупность наблюдённых значений
одинакова и равна s, то, для того чтобы совокупность наблюдённых значений 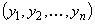 была наивероятнейшей, нужно выбрать функцию
была наивероятнейшей, нужно выбрать функцию 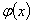 так, чтобы сумма квадратов отклонений наблюдённых значений
так, чтобы сумма квадратов отклонений наблюдённых значений 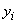 от
от 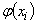 была минимальной:
была минимальной:
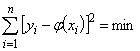 .
.
Способ согласования кривой 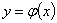 и экспериментальных точек, при котором выполняется это условие, носит название метода наименьших квадратов.Если из соображений, связанных с существом изучаемого явления или просто с внешним видом наблюдённой зависимости (расположения точек
и экспериментальных точек, при котором выполняется это условие, носит название метода наименьших квадратов.Если из соображений, связанных с существом изучаемого явления или просто с внешним видом наблюдённой зависимости (расположения точек  на плоскости), выбран общий вид функции
на плоскости), выбран общий вид функции 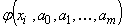 , зависящий от нескольких числовых параметров
, зависящий от нескольких числовых параметров 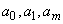 , и требуется выбрать
, и требуется выбрать 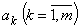 так, чтобы выполнялось условие
так, чтобы выполнялось условие
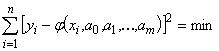 ,
,
то значения 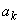 определятся из условий:
определятся из условий:
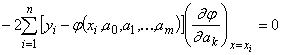
или
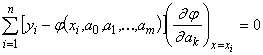 .
.
Составление и решение этой системы упрощается в случае, когда функция 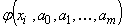 линейна относительно параметров. Тогда справедливо:
линейна относительно параметров. Тогда справедливо:
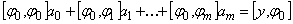 ;
;
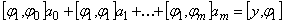
...
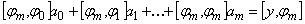 .
.
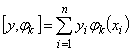 ;
; 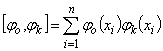 ;...;
;...; 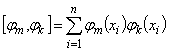 .
.
В частном случае при сглаживании полиномом 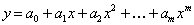 коэффициенты
коэффициенты 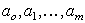 определятся из системы уравнений:
определятся из системы уравнений:
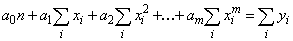 ;
;
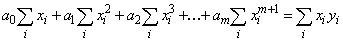 ;
;
…
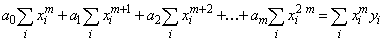 .
.
Рассмотренный подходиспользовалсядля установления связи между коэффициентами пластичности kпл и структуры kстр эпоксидных композитов (табл.1). Из расположения экспериментальных точек на плоскости при определении аналитической зависимости ограничились линейной зависимостью
kстр = a0 + a1 kпл, (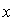 =kпл,
=kпл, 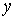 = kстр).
= kстр).
Таблица 1
|
kпл |
0,08 |
0,43 |
0,47 |
0,51 |
0,52 |
0,6 |
0,7 |
0,9 |
0,93 |
1,4 |
|
kстр |
16,1 |
13,2 |
14,8 |
14,2 |
13,8 |
14,2 |
7,8 |
14,5 |
15 |
5,4 |
Искомая зависимость определилась в виде
;
возможность ограничиться линейной корреляционной связью между kстр и kпл следует из 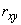 = — 0,68.
= — 0,68.
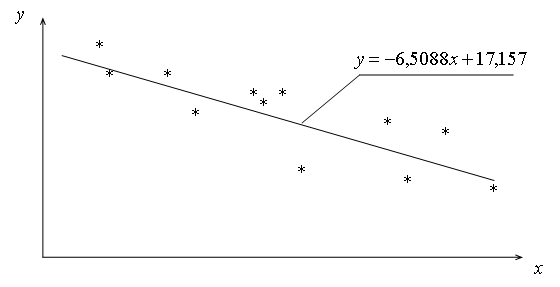 |
Рис.1.
Так же определялась зависимость влияния содержания водорода H [вес. ч.] в бетоне на толщину [см] защиты при расчёте, исходя из допустимой дозы излучений синхроциклотрона Xд, допустимого потока Xп при кратности ослабления 107 раз и плотности бетона 2350 кг/м3 (табл.2).
Таблица 2
|
H, вес. ч. |
0,1 |
0,35 |
0,61 |
0,81 |
1,09 |
|
Xд, см |
1005 |
991 |
983 |
980 |
975 |
|
Xп, см |
1133 |
1095 |
1077 |
1069 |
1060 |
Здесь линейная интерпретация дает большую погрешность. Поэтому были определены параметры квадратичной зависимости Xд от H. В соответствии с предыдущим была получена следующая искомая аналитическая зависимость в виде:
.
Для получения аналитических зависимостей часто используются и методы математического планирования эксперимента (полно- и дробно-факторные планы эксперимента, позволяющие получить интерполяционные полиномы во всем рассматриваемом факторном пространстве или его локальной области при существенном сокращении числа опытов в эксперименте).
Литература:
1. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. -2013. -№ 5. С. 42–45.
2. Будылина Е. А., Гарькина И. А., Данилов А. М., Пылайкин С. П. Подходы к многокритериальности сложных систем / Молодой ученый. -2013. -№ 6. С. 40–43.
3. Данилов А.М, Гарькина И. А. Методология проектирования сложных систем при разработке материалов специального назначения // Известия ВУЗов. Строительство, 2011 г. — № 1. — С.80–85.
4. Будылина Е. А., Гарькина И. А., Данилов А. М., Сухов Я. И. Некоторые подходы к анализу и синтезу сложных систем / «Молодой ученый. — № 10(57), 2013. — с.105–107.
5. Будылина Е. А., Гарькина И. А. Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. № 2(16). 2013. — C. 138–143.
6. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы управления / Региональная архитектура и строительство, № 1 (12), 2012. — С.39–43







