К основным целям обучения математике относится формирование умений строить математические модели простейших реальных явлений, исследовать явления по заданным моделям, конструировать приложения моделей. Одним из средств реализации этой цели является метод математического моделирования. Под математическим моделированием, в узком смысле слова, понимают описание в виде уравнений и неравенств реальных физических, химических, технологических, биологических, экономических и других процессов. Для того чтобы использовать математические методы для анализа и синтеза различных процессов, необходимо уметь описать эти процессы на языке математики, то есть описать в виде системы уравнений и неравенств. При построении модели используются такие операции мышления, как анализ через синтез, сравнение, классификация, обобщение, которые способствуют его развитию. Составление математической модели, перевод задачи на язык математики готовит студентов к моделированию реальных процессов и явлений в их будущей профессиональной деятельности. Особую роль математическое моделирование играет в экономической и научной сфере деятельности.
Рассмотрим применение математического моделирования при решении транспортных задач в экономике, а также математическую модель в задачах по теории цепей Маркова, в теории вероятностей. Чем и покажем значение математического моделирования в разных областях.
1. Математическое моделирование в экономике. Математическая модель транспортной задачи является математической моделью задачи линейного программирования. Среди множества решений системы ограничений необходимо найти такое неотрицательное решение, при котором целевая функция принимала бы минимальное значение. Как и любая другая задача линейного программирования, транспортная задача может быть решена при помощи симплекс-метода. Благодаря особому устройству системы ограничений общая процедура симплекс-метода в применении к транспортной задаче сильно упрощается. Хотя для транспортной задачи существуют несколько весьма простых и удобных методов отыскания начального допустимого решения (опорного плана). Транспортные задачи закрытого типа, когда запас груза на базах совпадает с объемом потребности предприятий, решаются двумя методами: северо-западного угла и минимальной стоимости. Транспортные задачи открытого типа, когда запасы превышают потребности или наоборот, сводятся к задачам закрытого типа путем введения фиктивного пункта назначения (в случае превышения груза на базах над общими потребностями предприятий) или фиктивного поставщика (в случае превышения спроса над запасами на базах).
Отметим, что процесс моделирования состоит из следующих этапов: 1) перевод предложенной задачи на язык математических терминов, то есть построение математической модели задачи (формализация); 2) решение задачи (решение внутри модели); 3) перевод полученного результата (математического решения) на язык, на котором была сформулирована исходная задача (интерпретация полученного решения).
Наиболее ответственным и сложным является первый этап — построение математической модели. Оно осуществляется логическим путем на основе анализа изучаемого явления (процесса) и требует умения описать явление (процесс) на языке математики. Второй этап — этап решения задачи в рамках математической теории можно еще назвать этапом математической обработки формальной модели. Он является решающим в математическом моделировании. Именно на этом этапе применяются все математические методы (логические, алгебраические, геометрические и т. д.) для формального вывода следствий из исходных допущений модели. На стадии математической обработки рассматриваются абстракции. Этот этап представляет собой дедуктивное ядро моделирования. На последнем этапе моделирования полученные выводы проходят через еще один процесс перевода — с языка математики обратно на естественный язык. Всё выше сказанное проиллюстрируем примером.
Пример. На базах имеется запас сырья необходимого для производства четырех предприятий. На первой базе — 60 т., на второй — 90 т., на третьей — 140 т. Первому предприятию для производства требуется 40 т. сырья, второму — 30 т., третьему — 100 т., четвертому — 120 т. Найти оптимальный план задачи методом северо-западного угла, зная, что стоимость перевозок с первой базы на первое предприятие равна 4 ед., на второе — 2 ед., на третье — 3 ед., на четвертое — 4 ед., со второй базы на первое предприятие равна 2 ед., на второе — 4 ед., на третье — 3 ед., на четвертое — 5 ед., с третьей базы на первое предприятие равна 6 ед., на второе — 5 ед., на третье — 4 ед., на четвертое — 6 ед.
I этап. Формализация. Построим математическую модель задачи в виде таблицы:
|
П Б |
П1 |
П2 |
П3 |
П4 |
Запасы |
|
Б1 |
4 |
2 |
3 |
4 |
60 |
|
Б2 |
2 |
4 |
3 |
5 |
90 |
|
Б3 |
6 |
5 |
4 |
6 |
140 |
|
Потребности |
40 |
30 |
100 |
120 |
290 290 |
II этап. Внутримодельное решение. Заполнение таблицы начнем с верхней левой клетки. Стоимость перевозки одной тонны груза с первой базы к первому потребителю равна 4. Перевезем с базы Б1 40 тонн груза на П1. И величину этой перевозки запишем в клетку (1,1). Потребности первого предприятия полностью удовлетворены. Запас на первой базе изменился — теперь это 20 тонн.
|
П Б |
П1 |
П2 |
П3 |
П4 |
Запасы |
|
Б1 |
4 40 |
2 |
3 |
4 |
20 |
|
Б2 |
2 |
4 |
3 |
5 |
90 |
|
Б3 |
6 |
5 |
4 |
6 |
140 |
|
Потребности |
30 |
100 |
120 |
290 290 |
Не рассматривая клетки первого столбца, снова берем левую верхнюю клетку из оставшихся. Это клетка (1,2). С первой базы перевезем оставшиеся 20 тонн на втрое предприятие. Его потребность не удовлетворена на 10 тонн.
|
П Б |
П1 |
П2 |
П3 |
П4 |
Запасы |
|
Б1 |
4 40 |
2 20 |
3 |
4 |
|
|
Б2 |
2 |
4 |
3 |
5 |
90 |
|
Б3 |
6 |
5 |
4 |
6 |
140 |
|
Потребности |
10 |
100 |
120 |
290 290 |
Помещаем в клетку (2,2) 10 тонн груза для второго предприятия, тем самым изменился запас на второй базе. Продолжая распределение, выбираем клетку (2,3). Направляем все 80 тонн со второй базы на третье предприятие. Оставшиеся 140 тонн с третьей базы распределяем соответственно на третье и четвертое предприятия. Получим окончательную таблицу, в которой необходимо проверить суммы поставок по строкам и столбцам.
|
П Б |
П1 |
П2 |
П3 |
П4 |
Запасы |
|
Б1 |
4 40 |
2 20 |
3 |
4 |
60 |
|
Б2 |
2 |
4 10 |
3 80 |
5 |
90 |
|
Б3 |
6 |
5 |
4 20 |
6 120 |
140 |
|
Потребности |
40 |
30 |
100 |
120 |
290 290 |
III этап. Интерпретация. Переведем результат с математического языка на язык исходной задачи. Число занятых клеток в составленном плане равно шести. Число базисных переменных также должно быть равно шести: 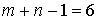 . Это означает, что полученный методом северо-западного угла план является опорным.
. Это означает, что полученный методом северо-западного угла план является опорным.
Как и в случае любого моделирования, математическая модель не описывает полностью изучаемое явление, и возникают вопросы о применимости полученных таким образом результатов. Существуют методы первоначального распределения поставок, связывающие выбор клетки с величиной издержек. Так, в методе минимальной стоимости на каждом этапе выбирается та клетка из свободных, которой соответствует минимальный коэффициент издержек. Например, в рассмотренном примере распределительная таблица, созданная по методу минимальной стоимости, выглядит следующим образом:
|
П Б |
П1 |
П2 |
П3 |
П4 |
Запасы |
|
Б1 |
4 |
2 30 |
3 30 |
4 |
60 |
|
Б2 |
2 40 |
4 |
3 50 |
5 |
90 |
|
Б3 |
6 |
5 |
4 20 |
6 120 |
140 |
|
Потребности |
40 |
30 |
100 |
120 |
290 290 |
Можно было бы ожидать, что в смысле близости к оптимуму допустимые решения, построенные с учетом затрат, будут лучше планов, построенных диагональным методом северо-западного угла. Однако на практике это не так. Необходимо обращать внимание студентов на то, что математическая модель и реальный процесс не тождественны между собой. Как правило, математическая модель строится с некоторым упрощением и при некоторой идеализации.
2. Математическое моделирование в теории вероятностей. Пусть производятся последовательные испытания, в каждом из которых может произойти одно и только одно из k несовместных событий 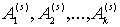 , образующих полную группу. Эта последовательность образует цепь Маркова, если условная вероятность в (s+1) –м испытании (s= 1, 2, 3,…) соответствует событию
, образующих полную группу. Эта последовательность образует цепь Маркова, если условная вероятность в (s+1) –м испытании (s= 1, 2, 3,…) соответствует событию 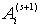 .
.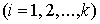 , после того как в s-м испытании, произошло событие известное нам, зависящее только от того, каким было событие, произошедшее в s-м испытании, и не изменяющееся от дополнительных сведений о том, какие события происходили в более ранних испытаниях. Чаще всего рассматриваются однородные цепи Маркова, в которых условная вероятность появления события
, после того как в s-м испытании, произошло событие известное нам, зависящее только от того, каким было событие, произошедшее в s-м испытании, и не изменяющееся от дополнительных сведений о том, какие события происходили в более ранних испытаниях. Чаще всего рассматриваются однородные цепи Маркова, в которых условная вероятность появления события 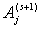 в (s+1)-м испытании при условии, что в s-м испытании осуществилось событие
в (s+1)-м испытании при условии, что в s-м испытании осуществилось событие 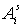 , не зависит от номера испытания. Эту вероятность назовем вероятностью перехода и обозначим буквой
, не зависит от номера испытания. Эту вероятность назовем вероятностью перехода и обозначим буквой 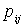 ; в этом обозначении первый индекс обозначает результат предшествующего испытания, а второй — указывает, в какое состояние перейдет система в последующий момент времени.
; в этом обозначении первый индекс обозначает результат предшествующего испытания, а второй — указывает, в какое состояние перейдет система в последующий момент времени.
Полная вероятностная картина возможных изменений, осуществляющихся при переходе от одного испытания к непосредственно следующему, задается матрицей
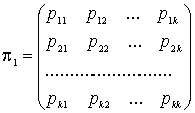
составленной из вероятностей перехода, называемой матрицей перехода. Рассмотрим примеры цепей Маркова и приведем их математическую модель.
Пример: Предположим, что частица находится на прямой и движется по этой прямой под влиянием случайных толчков, происходящих в моменты 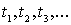 . Частица может находиться в точках с целочисленными координатами
. Частица может находиться в точках с целочисленными координатами 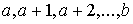 ; в точках
; в точках 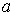 и
и 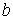 находятся отражающие стенки. Каждый толчок перемещает частицу вправо с вероятностью
находятся отражающие стенки. Каждый толчок перемещает частицу вправо с вероятностью 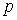 и влево с вероятностью
и влево с вероятностью 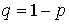 , при условии, что частица не находится у стенки. Если частица находится у стенки, то любой толчок переводит ее на единицу внутрь промежутка между стенками. Данный пример блуждания частицы представляет собой типичную цепь Маркова. Аналогично можно рассматривать случай, когда частица прилипает к одной из стенок или к обеим из них.
, при условии, что частица не находится у стенки. Если частица находится у стенки, то любой толчок переводит ее на единицу внутрь промежутка между стенками. Данный пример блуждания частицы представляет собой типичную цепь Маркова. Аналогично можно рассматривать случай, когда частица прилипает к одной из стенок или к обеим из них.
Напишем матрицу перехода для описанного примера, для случая частицы, блуждающей между двумя отражающими стенками, это будет нашей математической моделью. Если обозначим через 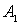 событие, состоящее в пребывании частицы в точке с координатой
событие, состоящее в пребывании частицы в точке с координатой 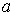 , через
, через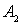 — пребывание в точке с координатой
— пребывание в точке с координатой 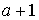 , …, через
, …, через 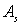
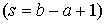 — пребывание в точке с координатой
— пребывание в точке с координатой 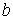 , то матрица перехода будет иметь вид (1).
, то матрица перехода будет иметь вид (1).
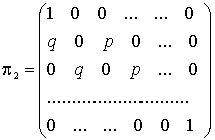
Так же приведем пример математической модели в виде матрицы перехода (2) для блуждания частицы между двумя поглощающими стенками. Обозначения событий и остальные условия сохраним те же, что и в предыдущем примере. Разница будет лишь в том, что частица, попавшая в состояния 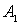 или
или 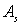 , остается в них с вероятностью равной единице.
, остается в них с вероятностью равной единице.
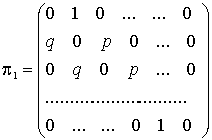 (1)
(1)
 (2)
(2)
Известно, что для решения задачи в рамках одной и той же модели может быть предложено много различных методов. В теории вероятностей и математической статистике хорошо известна история Центральной Предельной Теоремы, которая была получена многими различными методами, из которых напомним теорему Муавра-Лапласа, метод моментов Чебышева, метод характеристических функций Ляпунова, методы, примененные Линдебергом и Феллером. В настоящее время для решения практически важных задач могут быть использованы современные информационные технологии на основе метода статистических испытаний и соответствующих датчиков псевдослучайных чисел.
При решении задач посредством моделирования студенты учатся переводу жизненных проблемных ситуаций в абстрактные модели и наоборот. Использование моделирования способствует усилению творческой направленности процесса обучения, развитию умственных способностей, а тем самым развитию науки в целом.
Литература:
1. Акулич И. Л. Математическое программирование в примерах и задачах — М.: Высшая школа,1986. — 319 с.
2. Будылина Е. А., Гарькина И. А., Данилов А.М Моделирование с позиций управления в технических системах // Региональная архитектура и строительство. 2013. № 2 – С. 138–142.
3. Гнеденко Б. В. Курс теории вероятностей. — М.: Либроком, 2011. — 448 с.
4. Ермолаева Е. И. Математическое моделирование физических процессов в теории вероятностей // Актуальные проблемы гуманитарных и естественных наук. 2010. № 10 — С.13–14.
5. Козин Р. Г. Математическое моделирование. Примеры решения задач.- М.: МИФИ, 2010. — 177 с.







