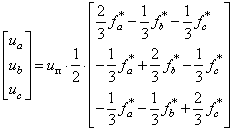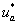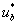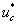В работе [1] рассматривался процесс математического моделирования асинхронного двигателя (2p = 2, Z1 = 6) на основе магнитных схем замещения. Питание обмотки индуктора (соединение «звезда» без нулевого провода, классический тип укладки обмотки) осуществлялось от источника трехфазного синусоидального напряжения.
В данной работе рассматривается процесс математического моделирования асинхронного двигателя (АД) при питании от трехфазного автономного инвертора напряжения с широтно-импульсной модуляцией (АИН ШИМ). Результаты этой работы будут основой для создания учебно-лабораторной установки по исследованию системы АИН ШИМ – АД.
Функциональная схема системы трехфазный автономный инвертор с ШИМ – асинхронный двигатель приведен на рис. 1.
В этой схеме приняты следующие обозначения:
- 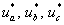 – задающие гармонические воздействия:
– задающие гармонические воздействия:
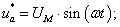
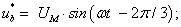
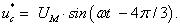
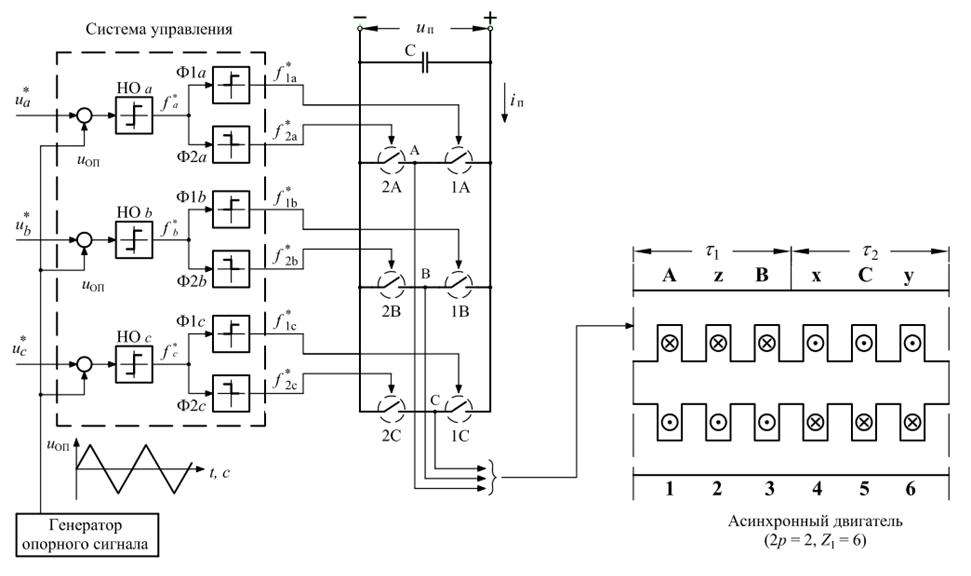
Рис. 1. Функциональная схема системы «АИН ШИМ – АД»
- uоп – опорное напряжение, представляющее собой пилообразное, двухстороннее, симметричное напряжение с частотой модуляции значительно превышающей частоту напряжения задания;
- НОа, НОb и НОс – нуль-органы, обеспечивающие сравнение сигналов задания с опорным сигналом. Если 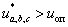 , то выходные сигналы нуль-органов
, то выходные сигналы нуль-органов 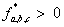 , иначе
, иначе 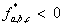 ;
;
-
|
- 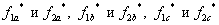 – дискретные выходные сигналы с формирователей, управляющих включением силовыми ключами.
– дискретные выходные сигналы с формирователей, управляющих включением силовыми ключами.
- 1А и 2А, 1В и 2В, 1С и 2С – силовые ключи попеременно подключающие обмотки фаз двигателя к разноименным полюсам источника постоянного напряжения uп.
Цифровой алгоритм расчета опорного сигнала ШИМ приведен в работе [3]. Программирование выходных сигналов нуль-органов произведен в MATLAB и имеет следующий вид:
dt=0.00001;
U0=1;
tau=0;
time=0;
u0p(1)=1;
pwm=-2;
f_sin=50;
f_triangle=1000;
for i=1:8000
tau(i+1)=tau(i)+dt*f_triangle;
time(i+1)=time(i)+dt;
s(i+1)=3*sin(2*pi*f_sin*time(i+1));
s_pi3(i+1)=3*sin(2*pi*f_sin*time(i+1)+pi/3);
if tau(i+1)>=1
tau(i+1)=tau(i+1)-1;
end
if (tau(i+1)>=0) && (tau(i+1)<0.5)
f(i)=1-4*tau(i+1);
else
f(i)=4*tau(i+1)-3;
end
u0p(i+1)=U0*f(i);
if (s(i+1)>=u0p(i+1))
pwm(i+1)=2;
else
pwm(i+1)=-2;
end
if (s_pi3(i+1)>=u0p(i+1))
pwm_pi3(i+1)=2;
else
pwm_pi3(i+1)=-2;
end
end
subplot(2,1,1);
plot(time,s,time,u0p,time,pwm);
hold on;
axis([0 0.04 -4 4]);
subplot(2,1,2);
plot(time,s_pi3,time,u0p,time,pwm_pi3);
hold on;
axis([0 0.04 -4 4]);
Результаты сравнений 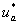 с
с 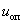 для двух значений (
для двух значений (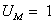 и
и 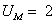 ) приведены на рис. 2 и 3 соответственно (сплошными линиями обозначены выходные сигналы
) приведены на рис. 2 и 3 соответственно (сплошными линиями обозначены выходные сигналы 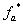 с нуль-органа).
с нуль-органа).
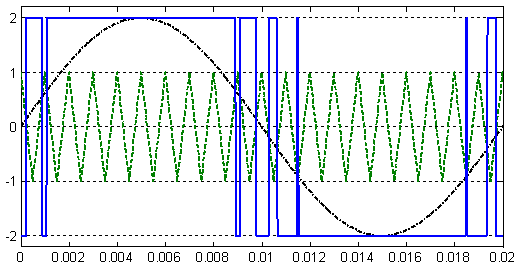
Рис. 2. Сигнал 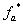 на выходе нуль-органа
на выходе нуль-органа 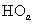 при
при 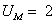
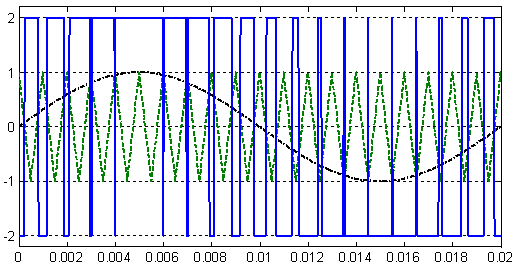
Рис. 3. Сигнал 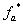 на выходе нуль-органа
на выходе нуль-органа 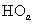 при
при 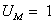
Формирователи сигналов управления силовыми ключами (Ф1а и Ф2а, Ф1b и Ф2b, Ф1с и Ф2с) задают программу подключения фаз обмоток двигателя к источнику постоянного напряжения uп.
Фазное напряжение в обмотке двигателя представляет собой пятиуровневую импульсную функцию [2] со значениями:
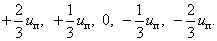
Импульсные напряжения подаваемые на двигатель 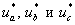 связаны с постоянным напряжением uп и выходными сигналами нуль-органов
связаны с постоянным напряжением uп и выходными сигналами нуль-органов 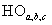
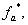 и
и 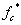 по следующей зависимости [2]:
по следующей зависимости [2]:
|
|
(*) |
Уравнения (*) для решения в программном пакете MATLAB примут следующий вид:
dt=0.00001;
U0=1;
tau=0;
time=0;
u0p(1)=1;
pwm=-1;
um=2;
f_sin=50;
f_triangle=1000;
Um=310/2;
up=Um/2;
for i=1:8000
tau(i+1)=tau(i)+dt*f_triangle;
time(i+1)=time(i)+dt;
s(i+1)=um*sin(2*pi*f_sin*time(i+1));
s_2pi3(i+1)=um*sin(2*pi*f_sin*time(i+1)+2*pi/3);
s_4pi3(i+1)=um*sin(2*pi*f_sin*time(i+1)+4*pi/3);
if tau(i+1)>=1
tau(i+1)=tau(i+1)-1;
end
if (tau(i+1)>=0) && (tau(i+1)<0.5)
f(i)=1-4*tau(i+1);
else
f(i)=4*tau(i+1)-3;
end
u0p(i+1)=U0*f(i);
if (s(i+1)>=u0p(i+1))
pwm(i+1)=2;
else
pwm(i+1)=-2;
end
if (s_2pi3(i+1)>=u0p(i+1))
pwm_2pi3(i+1)=2;
else
pwm_2pi3(i+1)=-2;
end
if (s_4pi3(i+1)>=u0p(i+1))
pwm_4pi3(i+1)=2;
else
pwm_4pi3(i+1)=-2;
end
PWM(i+1)=up*(1/2)*((2*(pwm(i+1)))/3-(pwm_2pi3(i+1))/3-(pwm_4pi3(i+1))/3);
PWM_2pi3(i+1)=up*(1/2)*(-pwm(i+1)/3+(2*pwm_2pi3(i+1))/3-pwm_4pi3(i+1)/3);
PWM_4pi3(i+1)=up*(1/2)*(-pwm(i+1)/3-pwm_2pi3(i+1)/3+(2*pwm_4pi3(i+1))/3);
end
plot(time,PWM);
axis([0 0.02 -250 250]);
Результаты расчета фазного напряжения 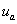 для задающих сигналов с
для задающих сигналов с 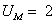 и
и 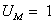 приведены на рис. 4 и 5 соответственно.
приведены на рис. 4 и 5 соответственно.
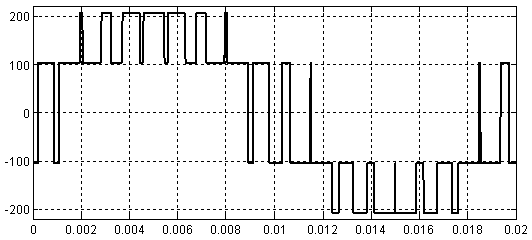
Рис. 4. Импульсное напряжение в фазе обмотки 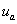 при амплитуде задающего сигнала
при амплитуде задающего сигнала 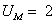
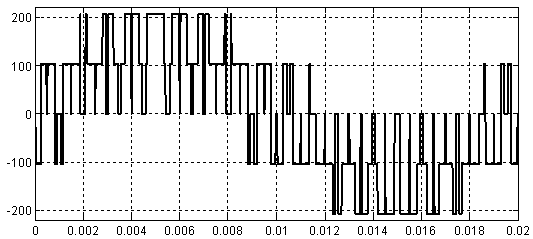
Рис. 5. Импульсное напряжение в фазе обмотки 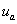 при амплитуде задающего сигнала
при амплитуде задающего сигнала 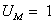
Одна из возможных реализаций математической модели системы «АИН ШИМ –АД» на языке высокого уровня MATLAB примет следующий вид:
% Математическая модель расчета асинхронного двигателя с помощью магнитных
% схем замещения методом Гаусса-Жордана
function AD
% Начальные условия
Rb=0.1003*10^7;
rs=19/2;
Ls=0.074/2;
rr=(9.269*10^-5)/2;
Lr=(0.0372*10^-5);
dt=0.00001;
tz=(9.769*10^-3);
m=1.9;
v0=0;
wn=200;
f=50;
w=2*pi*f;
U=wn/dt;
Um=310/2;
up=Um*0.5;
X=zeros(9,1);
F=0;
U0=1;
tau=0;
time=0;
u0p(1)=1;
um=2;
pwm=-1;
f_triangle=1000;
f_sin=50;
K=input('длительность цикла k=');
for k=1:(K+1)
% ШИМ
tau(k+1)=tau(k)+dt*f_triangle;
time(k+1)=time(k)+dt;
s(k+1)=um*sin(2*pi*f_sin*time(k+1));
s_2pi3(k+1)=um*sin(2*pi*f_sin*time(k+1)+2*pi/3);
s_4pi3(k+1)=um*sin(2*pi*f_sin*time(k+1)+4*pi/3);
if tau(k+1)>=1
tau(k+1)=tau(k+1)-1;
end
if (tau(k+1)>=0) && (tau(k+1)<0.5)
f(k)=1-4*tau(k+1);
else
f(k)=4*tau(k+1)-3;
end
u0p(k+1)=U0*f(k);
if (s(k+1)>=u0p(k+1))
pwm(k+1)=2;
else
pwm(k+1)=-2;
end
if (s_2pi3(k+1)>=u0p(k+1))
pwm_2pi3(k+1)=2;
else
pwm_2pi3(k+1)=-2;
end
if (s_4pi3(k+1)>=u0p(k+1))
pwm_4pi3(k+1)=2;
else
pwm_4pi3(k+1)=-2;
end
PWM(k+1)=up*(1/2)*((2*(pwm(k+1)))/3-(pwm_2pi3(k+1))/3-(pwm_4pi3(k+1))/3);
PWM_2pi3(k+1)=up*(1/2)*(-pwm(k+1)/3+(2*pwm_2pi3(k+1))/3-pwm_4pi3(k+1)/3);
PWM_4pi3(k+1)=up*(1/2)*(-pwm(k+1)/3-pwm_2pi3(k+1)/3+(2*pwm_4pi3(k+1))/3);
PWM_linear(k+1)=sqrt(3)*PWM(k+1);
PWM_2pi3_linear(k+1)=sqrt(3)*PWM_2pi3(k+1);
v(1,k)=v0; % создание вектор-строки для графика скорости
f(1,k)=sum(F);
% создание матрицы А
A=zeros(9);
B=2*Rb*(rr+Lr/dt)+1/dt;
C=-Rb*(rr+Lr/dt)+(2*Rb*Lr+1)*v0/(2*tz);
D=-Rb*Lr*v0/(2*tz);
E=-Rb*(rr+Lr/dt)-(2*Rb*Lr+1)*v0/(2*tz);
T=-wn*Lr*v0/(2*tz);
Y=-wn*(rr+Lr/dt);
W1=-wn*Lr/dt;
P=-Rb*Lr/dt;
Q=(2*Rb*Lr+1)/dt;
KS=rs+Ls/dt;
% Матрица А
% n=1
A(1,1)=B;
A(1,2)=C;
A(1,3)=D;
A(1,5)=-D;
A(1,6)=E;
A(1,7)=Y;
A(1,8)=-T;
A(1,9)=T;
% n=2
A(2,1)=E;
A(2,2)=B;
A(2,3)=C;
A(2,4)=D;
A(2,6)=-D;
A(2,7)=-T;
A(2,8)=-Y;
A(2,9)=T;
% n=3
A(3,1)=-D;
A(3,2)=E;
A(3,3)=B;
A(3,4)=C;
A(3,5)=D;
A(3,7)=-T;
A(3,8)=T;
A(3,9)=Y;
% n=4
A(4,2)=-D;
A(4,3)=E;
A(4,4)=B;
A(4,5)=C;
A(4,6)=D;
A(4,7)=-Y;
A(4,8)=T;
A(4,9)=-T;
% n=5
A(5,1)=D;
A(5,3)=-D;
A(5,4)=E;
A(5,5)=B;
A(5,6)=C;
A(5,7)=T;
A(5,8)=Y;
A(5,9)=-T;
% n=6
A(6,1)=C;
A(6,2)=D;
A(6,4)=-D;
A(6,5)=E;
A(6,6)=B;
A(6,7)=T;
A(6,8)=-T;
A(6,9)=-Y;
% n=7
A(7,1)=U;
A(7,3)=-U;
A(7,4)=-U;
A(7,6)=U;
A(7,7)=KS;
A(7,9)=-KS;
% n=8
A(8,2)=U;
A(8,3)=U;
A(8,5)=-U;
A(8,6)=-U;
A(8,8)=-KS;
A(8,9)=KS;
% n=9
A(9,7)=1;
A(9,8)=1;
A(9,9)=1;
% Матрица свободных членов
S=[W1*X(7)+P*(X(6)+X(2))+Q*X(1);
W1*(-1)*X(8)+P*(X(1)+X(3))+Q*X(2);
W1*X(9)+P*(X(2)+X(4))+Q*X(3);
W1*(-1)*X(7)+P*(X(3)+X(5))+Q*X(4);
W1*X(8)+P*(X(4)+X(6))+Q*X(5);
W1*(-1)*X(9)+P*(X(5)+X(1))+Q*X(6);
U*(X(1)-X(4)+X(6)-X(3))+(Ls/dt)*(X(7)-X(9))+PWM_2pi3_linear(k+1);
U*(X(3)-X(6)+X(2)-X(5))+(Ls/dt)*(X(9)-X(8))+PWM_linear(k+1);
0];
% Решение методом Гаусса-Жордана
Z=rref([A S]); % Приведение расширенной матрицы к треугольному виду
X=Z(1:9,10:10); % Выделение последнего столбца из матрицы
% Матрица токов ротора
Ir=[-wn*X(7)-Rb*X(6)+2*Rb*X(1)-Rb*X(2);
-wn*(-1)*X(8)-Rb*X(1)+2*Rb*X(2)-Rb*X(3);
-wn*X(9)-Rb*X(2)+2*Rb*X(3)-Rb*X(4);
-wn*(-1)*X(7)-Rb*X(3)+2*Rb*X(4)-Rb*X(5);
-wn*X(8)-Rb*X(4)+2*Rb*X(5)-Rb*X(6);
-wn*(-1)*X(9)-Rb*X(5)+2*Rb*X(6)-Rb*X(1)];
% Электромагнитное усилие
F=[(X(2)-X(6))*Ir(1)/(2*tz);
(X(3)-X(1))*Ir(2)/(2*tz);
(X(4)-X(2))*Ir(3)/(2*tz);
(X(5)-X(3))*Ir(4)/(2*tz);
(X(6)-X(4))*Ir(5)/(2*tz);
(X(1)-X(5))*Ir(6)/(2*tz)];
% Скорость
v0=v0+(sum(F)/m)*dt;
end;
% Построение графиков
k=0:(K);
subplot(2,1,1); plot(k*dt,v);title('Скорость');
xlabel('t, c');ylabel('v, м/c');grid on
subplot(2,1,2);plot(k*dt,f);title('Электромагнитное усилие');
xlabel('t,c');ylabel('F, H');grid on
end
В таблице 1 приведены идентификаторы, применяемые для математического моделирования системы «АИН ШИМ – АД» в MATLAB, в соответствии с обозначениями, приведенными на функциональной схеме рис. 1.
Таблица 1
Таблица идентификаторов
|
Наименование |
Обозначение на функциональной схеме |
Идентификатор |
|
Сигнал задания в фазах a,b,c |
|
s |
|
|
s_2pi3 |
|
|
|
s_4pi3 |
|
|
Выходные сигналы нуль-органов НОа, НОb и НОc |
|
pwm |
|
pwm_2pi3 |
||
|
|
pwm_4pi3 |
|
|
Импульсные напряжения на обмотках фаз двигателя А, В, С |
ua |
PWM |
|
ub |
PWM_2pi3 |
|
|
uc |
PWM_4pi3 |
Временные зависимости скорости и электромагнитного усилия асинхронного двигателя при питании от АИН для случаев с амплитудой напряжения питания Uм = 2 и Uм = 1 приведены на рис. 6 и 7 соответственно.
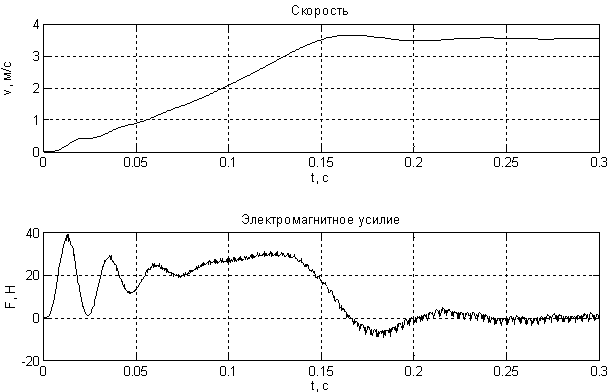
Рис. 6. Результат моделирования асинхронного двигателя при 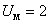
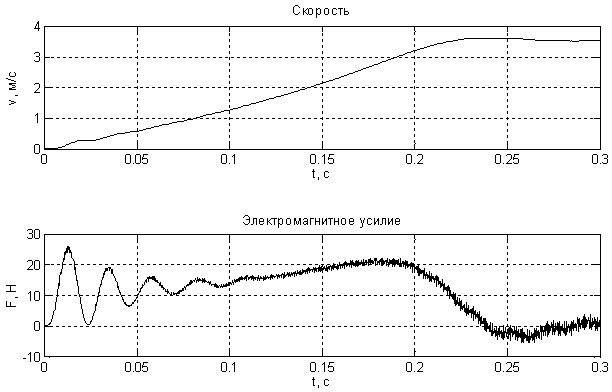
Рис. 7. Результат моделирования асинхронного двигателя при 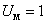
Литература:
1. Емельянов А.А. и др. Моделирование асинхронного двигателя с помощью магнитных и электрических схем замещения / Емельянов А.А., Медведев А.В., Кобзев А.В., Бочкарев Ю.П., Евдокимов О.В. // Молодой ученый. – 2013. – №4. – С. 1-10.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. – 654 с.
3. Емельянов А.А. и др. Моделирование системы АИН ШИМ – линейный асинхронный двигатель (Z1 = 6) с обмоткой индуктора через ярмо / Емельянов А.А., Медведев А.В., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Бочкарев Ю.П., Авдеев А.С., Чернов М.В., Габзалилов Э.Ф., Киряков Г.А. // Молодой ученый. – 2013. – №11. – С. 18-28.