Рассматривается задача исследования устойчивости двух разностных схем для численного решения уравнения колебаний балки. Исследование проводится методом Неймана. Выводятся соотношения зависимости шага по времени от шагов по пространственным переменным для того, чтобы использование разностной схемы приводило к решению.
Ключевые слова: балка, уравнение колебаний, разностная схема, устойчивость, Нейман, численное решение.
Введение. Большинство задач математической физики являются очень сложными для решения их аналитическим способом, например, задачи гашения колебаний элементов механических структур [1–14]. Поэтому огромное практическое значение имеет умение решать такие задачи численным способом, то есть аппроксимация исходной задачи конечно разностными схемами. Подобные методики дают приближённое решение, которое при увеличении точности стремится к аналитическому решению. Но чтобы такое происходило, необходимо, чтобы конечно разностные схемы были устойчивыми. Поэтому не менее значимым в вычислительной математике является нахождение условий, при которых конечно разностные схемы, полученные при аппроксимации исходной задачи, обладают условием устойчивости.
В этой работе будет показано, как найти такие условия устойчивости для двух возможных вариантов численного решения уравнения колебаний балки.
Исследование устойчивости первой конечно разностной схемы для численного решения уравнения колебаний балки. Колебания балки описываются гиперболическим по Петровскому уравнением
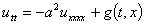 ,
, 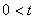 ,
,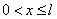 ,
,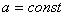 (1)
(1)
Начальные отклонения и скорость перемещения балки
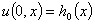 ,
, 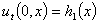 , (2)
, (2)
будем рассматривать как начальные условия. На концах балки наложим условия нежёсткого закрепления
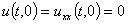 ,
, 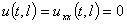 . (3)
. (3)
Уравнение (1) можно свести к системе двух уравнений второго порядка
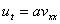 , (4)
, (4)
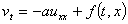 , (5)
, (5)
где
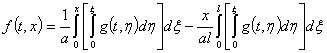 (6)
(6)
В связи с переходом к системе уравнений (4), (5) начальные и граничные условия (2), (3) преобразуются. Условия
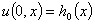 , (7)
, (7)
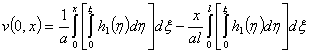 (8)
(8)
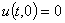 ,
, 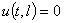 ,
, 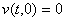 ,
, 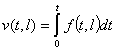 . (9)
. (9)
В силу того, что здесь ставится задача исследования устойчивости конечно разностной схемы, дальнейшие выкладки, с которыми можно ознакомиться здесь [1–14], будут опущены.
Построим разностную схему для приближённого решения системы (4), (5). Зададим натуральные числа 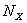 и
и 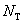 , и разобьём рассматриваемую область
, и разобьём рассматриваемую область 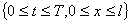 на прямоугольные ячейки параллельными прямыми
на прямоугольные ячейки параллельными прямыми 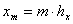 ,
, 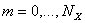 ,
, 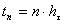 ,
, 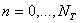 , где
, где 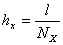 и
и 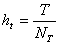 . В результате этих операций мы можем записать следующее
. В результате этих операций мы можем записать следующее
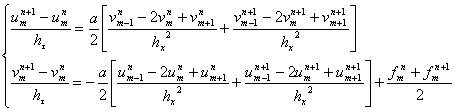 (10)
(10)
Как уже говорилось, в силу того, что здесь ставится задача исследования устойчивости конечно разностной схемы, некоторые выкладки будут опущены [1–14].
Сделаем элементарные преобразования в (10)
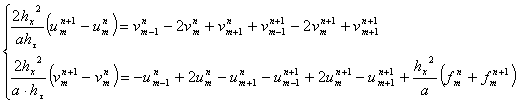 (11)
(11)
и пусть 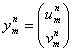 ,
, 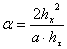 ,
, 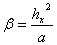 , которые мы подставим в (11). Умножим (11), приведённое к матричной форме, слева на матрицу
, которые мы подставим в (11). Умножим (11), приведённое к матричной форме, слева на матрицу 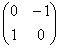 . Для более удобного понимания приведём элементарные расчёты. Собрав все подобные слагаемые и введя следующие обозначения
. Для более удобного понимания приведём элементарные расчёты. Собрав все подобные слагаемые и введя следующие обозначения 
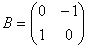 и
и 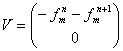 , в результате получим
, в результате получим
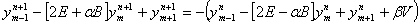 , (12)
, (12)
где 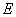 — единичная матрица.
— единичная матрица.
Покажем теперь, что схема (10) является безусловно устойчивой. Для этого рассмотрим однородное уравнение (10)
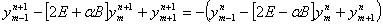 (13)
(13)
и воспользуемся спектральным признаком устойчивости Неймана [15]. Подставим 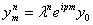 в (34), где
в (34), где 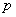 — параметр, а
— параметр, а 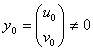 . В результате подстановки получим
. В результате подстановки получим
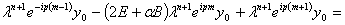
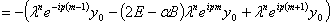 (14)
(14)
Делая элементарные преобразования, получаем
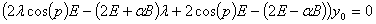 (15)
(15)
Так как 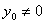 , то должен быть равен 0 определитель
, то должен быть равен 0 определитель
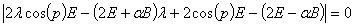 (16)
(16)
Проделаем следующие преобразования
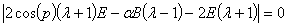 (17)
(17)
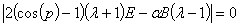 (18)
(18)
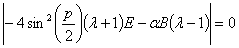 (19)
(19)
Теперь, вспоминая значение матрицы 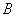 , можем записать
, можем записать
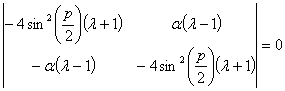 (20)
(20)
Раскрывая определитель (20), мы получаем выражение
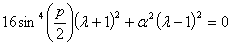 (21)
(21)
Делая элементарные преобразования
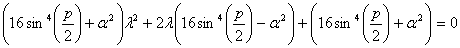 (22)
(22)
получаем
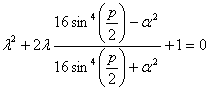 (23)
(23)
Если 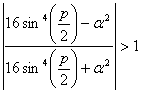 , то у нас есть 2 вещественных корня. По теореме Виета их произведение равняется 1. Следовательно, значение одного из них меньше единицы, а значение другого — больше. Этот случай нас не устраивает. Если
, то у нас есть 2 вещественных корня. По теореме Виета их произведение равняется 1. Следовательно, значение одного из них меньше единицы, а значение другого — больше. Этот случай нас не устраивает. Если 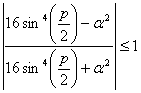 , тогда
, тогда 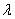 — комплексные и, следовательно,
— комплексные и, следовательно, 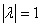 . Этот случай нам подходит. А так как
. Этот случай нам подходит. А так как
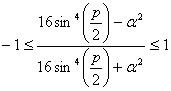 , (24)
, (24)
то мы получаем неравенство
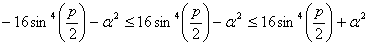 , (25)
, (25)
которое выполняется для любых 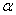 , т. е. для любых
, т. е. для любых 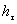 и
и 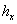 . Следовательно, схема (10) является безусловно устойчивой.
. Следовательно, схема (10) является безусловно устойчивой.
Приведём примеры применения конечно разностной схемы (10). При численном решении будут заданы следующие входные параметры 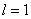 ,
, 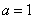 ,
, 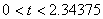 ,
,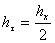 ,
, 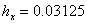 ,
, 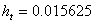 .
.
Пример 1. Рассмотрим однородное уравнение (10) и пусть начальное отклонение задаётся как 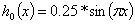 , скорость распространения будет
, скорость распространения будет 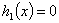 . На рис. 1 изображена функция колебания балки
. На рис. 1 изображена функция колебания балки 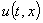 в трёхмерном виде
в трёхмерном виде
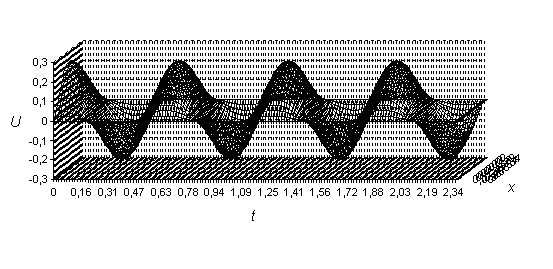
Рис. 1. Процесс колебания балки при первом численном способе решения
Исследование устойчивости второй конечно разностной схемы для численного решения уравнения колебаний балки. Для решения исходной задачи также можно было использовать другой численный метод.
Уравнение (1) можно представить в виде следующей системы, отличной от системы (4)-(5)
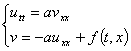 (26)
(26)
где 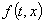 определяется по аналогии с (27)
определяется по аналогии с (27)
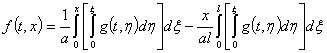 (27)
(27)
Граничные условия при переходе к системе (26) примут следующий вид
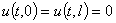 ,
, 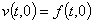 ,
, 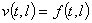 . (28)
. (28)
Далее представим систему (26) в виде конечно-разностной схемы
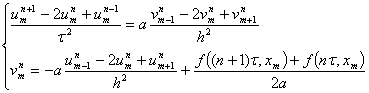 (29)
(29)
Из так определённой схемы возникает вопрос, как мы сможем определить значение на 1 слое (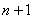 слой при
слой при 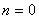 ), если нам необходимо значение
), если нам необходимо значение 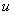 на -1 слоя. Для этого воспользуемся вторым условием в (2) и аппроксимируем его следующим образом
на -1 слоя. Для этого воспользуемся вторым условием в (2) и аппроксимируем его следующим образом
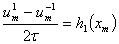 (30)
(30)
Из (30) следует следующее выражение
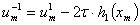 (31)
(31)
Таким образом, из первого уравнения системы (29) для слоя 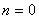 у нас получается, что
у нас получается, что
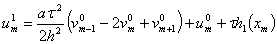 (32)
(32)
Теперь со слоя 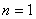 мы можем воспользоваться общей формулой, получающейся из той же системы (29)
мы можем воспользоваться общей формулой, получающейся из той же системы (29)
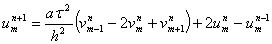 (33)
(33)
Покажем, что схема (29) устойчива воспользовавшись спектральным признаком устойчивости Неймана [15]. Подставим 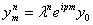 в однородное уравнение (29), где
в однородное уравнение (29), где 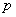 — параметр, а
— параметр, а 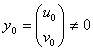 . В результате подстановки получим следующее выражение
. В результате подстановки получим следующее выражение
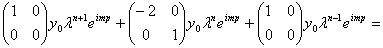
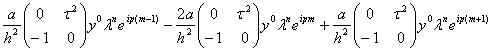 (34)
(34)
Далее разделим выражение (34) на значение 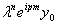 , тогда можно переписать следующим образом
, тогда можно переписать следующим образом
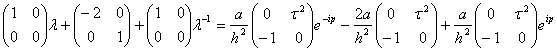 (35)
(35)
Соберём в (35) подобные слагаемые, тогда можно переписать следующим образом
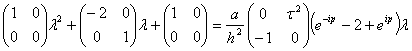 (36)
(36)
Вспоминая формулу Эйлера
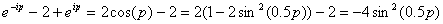 , (37)
, (37)
можем получить следующую систему уравнений
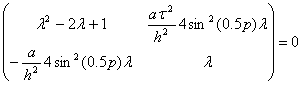 (38)
(38)
Эта система (38) имеет единственное решение, если её определитель равен нулю.
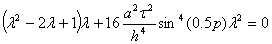 (39)
(39)
Одно из решений это значение 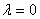 , но оно нас не устраивает, поэтому, разделив (39) на значение
, но оно нас не устраивает, поэтому, разделив (39) на значение 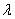 , получим
, получим
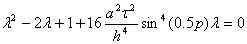 (40)
(40)
Это выражение можно переписать в квадратное уравнение следующего вида
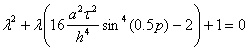 (41)
(41)
По теореме Виета нас интересует следующее условие
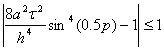 (42)
(42)
От куда можно выразить
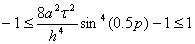 (43)
(43)
Тогда получим следующее выражение
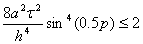 (44)
(44)
Что эквивалентно
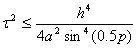 (45)
(45)
И окончательно получаем
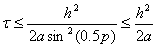 (46)
(46)
Таким образом, мы видим, что разностная схема (50) устойчива при выполнении условия (67), которое задаёт необходимое соотношение шагов в разностной схеме.
Приведём примеры применения разностной схемы (29). При численном решении будут заданы следующие входные параметры 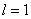 ,
, 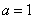 ,
, 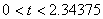 ,
,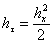 , при этом положим
, при этом положим 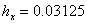 , тогда
, тогда 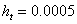 , тогда у нас получится 4800 точек по шкале времени.
, тогда у нас получится 4800 точек по шкале времени.
Пример 2. Рассмотрим однородное уравнение (29) и пусть начальное отклонение задаётся как 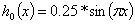 , скорость распространения будет
, скорость распространения будет 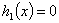 . На рис. 2 изображена функция колебания балки
. На рис. 2 изображена функция колебания балки 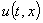 в трёхмерном виде
в трёхмерном виде
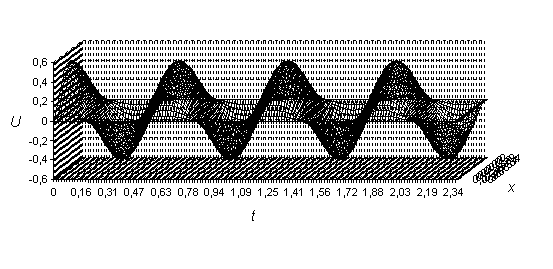
Рис. 2. Процесс колебания балки при втором способе численного решения.
Литература:
1. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А.. О гашении колебаний балки. // Труды ИСА РАН. Динамика неоднородных систем. Том 50(1). — М.: Книжный дом «ЛИБРОКОМ», 2010. — С. 53–58.
2. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А. О гашении колебаний сложных механических структур // Авиакосмическая техника и технология, 2012, № 4. С. 54–59.
3. Атамуратов А. Ж. О гашении колебаний прямоугольной мембраны // Вестник Тверского государственного университета. Серия Прикладная математика. — 2013. — № 2. — С. 49–59.
4. Атамуратов А. Ж. Исследование подходов к решению задач математической физики на примере уравнения колебаний прямоугольной мембраны // Молодой ученый. № 10. 2013. С. 1–5. http://www.moluch.ru/archive/57/6198/
5. Атамуратов А. Ж. Приведение к тригонометрической проблеме моментов на примере задачи гашения колебаний прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. № 11. 2013. С. 6–10. http://www.moluch.ru/archive/58/8092/
6. Атамуратов А. Ж. Получение интегралов энергии для прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. № 11. 2013. С. 10–15. http://www.moluch.ru/archive/58/8112/
7. Атамуратов А. Ж., Михайлов И. Е. Численное решение задачи о гашении колебаний балки. Тезисы докладов Международной конференции по прикладной математике и информатике, посвященной 100-летию со дня рождения академика А. А. Дородницына. ВЦ РАН, Москва, 7–11 декабря 2010 г. С. 83–84.
8. Muravey L., Mikhailov I., Atamuratov A., The damping problem of vibrations for large mechanical systems // ICIAM2011, Abstracts, Vancouver, Canada, July 18–22, 2011. P. 87.
9. Atamuratov A., Mikhailov I., Muravey L. On the numerical damping of beam’s vibrations // VII International Aerospace Congress IAC’12. Abstracts. Moscow, Russia. 26–31 August, 2012. P. 31–32.
10. Атамуратов А. Ж. Решение уравнения колебаний балки. // XXXV ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции. Москва, апрель 2008 г. Москва: МАТИ, 2008. Т.5.
11. Атамуратов А. Ж. О гашении колебаний балки. // XXXVI ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции. Москва, апрель 2010 г. Москва: МАТИ, 2010. Т.5.
12. Атамуратов А. Ж. О гашении колебаний прямоугольной мембраны. // XXXVII ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 8 томах. Москва, 5–8 апреля 2011 г. Москва: МАТИ, 2011. Т.5, С. 60–61
13. Атамуратов А. Ж. Решение уравнения колебаний круглой пластины. // XXXVIII ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 8 томах. Москва, 10–14 апреля 2012 г. Москва: МАТИ, 2012. Т.5, С. 38–39
14. Атамуратов А. Ж. Численный метод решения колебаний прямоугольной пластины. // XXXIX ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 9 томах. Москва, 9–13 апреля 2013 г. Москва: МАТИ, 2013. Т.5, С. 32–33
15. Самарский А. А., Гулин А. В. Численные методы. Москва: Наука, 1989. 432 с.







