В статье рассматривается задача о школьном автобусе, при ограничениях на вместимость транспортных средств — автобусов и на количество учеников. Построена соответствующая математическая модель. Разработан эвристический алгоритм решения задачи. Разработанный алгоритм реализован программно, приведен численный эксперимент на основе реальных данных, который показал эффективность разработанного метода.
Введение
Задача о школьном автобусе (SchoolBusRoutingProblem, SBRP) входит в класс задач маршрутизации. В ней необходимо подвезти учеников в школу или развести их по домам.
Рассматриваемая задача обладает практической ценностью: дети из маленьких деревень вынуждены учиться в школах находящихся в других населенных пунктах, а расстояния между деревнями большие и самостоятельные передвижения детей небезопасны, перед властями встает задача организации централизованной перевозки детей. В данном случае, нахождение оптимальных маршрутов, составление плана подвоза (развоза) учеников может существенно снизить расходы, связанные с организацией перевозок. Кроме того, SBRP может быть применена не только там, где необходимо развозить учащихся — решения SBRP может внести существенный вклад в экономию средств для предприятий, которые находятся за чертой города и привозят на работу (развозят по домам) работников.
1. Описание задачи о школьном автобусе
Задача о школьном автобусе (SchoolBusRoutingProblem, SBRP) изучается с момента ее первого упоминания в литературе [1]. Однако, несмотря на такой большой срок исследования, до сих пор остается необходимость общего подхода к решению SBRP, так как большинство исследований в этой области проводились в связи с появлением в реальном мире проблем с определенными допущениями и ограничениями. LiandFu[2] указывали, что не существует единственного преимущественного подхода для изучения SBRP. Более того, они добавили, что разнообразность подходов вытекает из разнообразия задач.
SBRPможно условно разделить на 5 подзадач [3]:
1. Подготовка данных (DataPreparation);
2. Выбор автобусных остановок (BusStopSelection);
3. Формирование автобусных маршрутов (BusRouteGeneration);
4. Установление времени звонка (School Bell Time Adjustment);
5. Расписание времени маршрутов (RouteScheduling).
В большинстве существующих подходов решения SBRP эти подзадачи рассматриваются отдельно и последовательно. Но связано это не с тем, что они не зависят друг от друга (они сильно взаимосвязаны), а со сложностью и большой размерностью задач.
Задача о школьном автобусе — это уникальная и независимая задача, хотя, отдельные ее подзадачи или их комбинации можно рассматривать как вариации уже существующих оптимизационных задач. Так, задача формирования автобусных маршрутов (Bus Route Generation) очень схожа с задачей транспортной логистики (Vehicle Routing Problem, VRP). Транспортная логистика стремится создать эффективный набор маршрутов для парка транспортных средств, с целью доставки товаров из одного или нескольких депо покупателям [4].
Пусть имеется начальный пункт — школа, S остановок, на которых нужно высадить учеников. Имеется R автобусов, которые имеют одинаковую вместимость Q. Количество учеников равно суммарной вместимости всех автобусов. Дороги характеризуются одним параметром — расстоянием. Автобусы выезжают из начального пункта — школы и не должны возвращаться обратно. Требуется найти такой набор маршрутов[1], чтобы развезти всех учеников по остановкам, при этом минимизировать расстояние, которое проезжает автобус для высадки ученика на последней остановке самого длинного маршрута.
Введем следующие обозначения
Дано:
Школа;
S — количество остановок;
R — количество автобусов;
Q — вместимость автобусов;
R*Q — количество учеников;
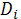 — количество учеников, которое нужно высадить на i-ой остановке, i=1,..,S;
— количество учеников, которое нужно высадить на i-ой остановке, i=1,..,S;
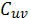 — расстояние (время) от пункта u до пункта v, u=1,..,S+1, v=1,..,S+1.
— расстояние (время) от пункта u до пункта v, u=1,..,S+1, v=1,..,S+1.
Найти:
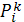 — количество учеников, которое k-ый автобус высаживает на i-ой остановке, k=1,..,R, i=1,..,S;
— количество учеников, которое k-ый автобус высаживает на i-ой остановке, k=1,..,R, i=1,..,S;
L(V) — минимальное из расстояний, которое проезжает автобус, развозя пассажиров по остановкам, V — множество остановок.
Задача имеет следующий вид:
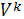 — подмножество остановок, которые должен посетить k-ый автобус, k=1,..,R.
— подмножество остановок, которые должен посетить k-ый автобус, k=1,..,R.
Найти числа 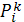 , k=1,..,R, i=1,..,S, такие что
, k=1,..,R, i=1,..,S, такие что
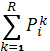 =
=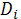 ; (1)
; (1)
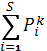 =Q; (2)
=Q; (2)
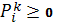 ,
, 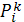 — целые; (3)
— целые; (3)
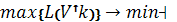 ; (4)
; (4)
Условие (1) отражает, что суммарное число пассажиров, которое автобусы высаживают на i-ой остановке должно быть равно числу пассажиров, которое необходимо доставить на i-ую остановку. Условие (2) указывает, что суммарное число пассажиров, попавших в автобус, не может превышать вместимости данного автобуса, условие (3) — из всех R автобусов пассажиры только высаживаются на остановках. Целевая функция (4) отражает, что необходимо минимизировать длину максимального маршрута.
Также, следует учесть, что на количество учеников накладывается условие целочисленности. В данном случае оно отражает физическую неделимость объектов — число учеников, которых нужно высадить на остановках не может быть равно 10.5 человек.
4. Алгоритм решения
Решение поставленной задачи можно условно разделить на 2 этапа:
1. Поиск кратчайших расстояний от школы до остановок;
2. Построение маршрутов автобусов для развоза учеников по домам, нахождение длин маршрутов.
Первый этап решается путем применение алгоритма Дейкстры, второй — с помощью алгоритма описанного ниже.
Учитывая, что целью задачи является развоз учеников по домам, можно сказать, что алгоритм, применяемый на втором этапе, работает как бы в обратном направлении — учеников забирают с остановок и привозят в школу. Это происходит следующим образом:
Находится самая дальняя остановка. Автобус забирает учеников с этой остановки и далее с остановок, находящихся на пути следования автобуса в школу. Если следующей остановкой на пути автобуса является школа, а автобус заполнен не полностью, рассматривается последняя посещенная остановка. Если от этой остановки существуют дороги до других остановок (далее — соседей), еще не посещенных автобусом, то из всех соседей выбирается та, до которой расстояние наименьшее. Автобус едет туда и забирает учеников. В случае, если автобус все еще не заполнен процедура поиска соседей возобновляется. Если автобус заполнен, или доступных остановок больше нет, автобус едет в школу. Таким образом, расстояние проеденное автобусом известно после того, как автобус приезжает в школу. Сам маршрут — последовательность остановок для развоза учеников по домам — получается в результате перестановки посещенных остановок в обратном порядке. Таким образом, отправным пунктом в маршруте у всех автобусов будет школа, на борту автобусов будет столько учеников, сколько они должны развести на данном маршруте и последним пунктом каждого маршрута будет какая-либо остановка, что отражает условие задачи — автобусам не нужно возвращаться в школу.
Для решения поставленной задачи был разработан программный продукт (ПП) в среде TurboPascal 7.0.
5. Проведение численного эксперимента
5.1. Постановка задачи
Для проведения численного эксперименты использовались реальные данные — расстояние между пунктами — это реальные расстояния между населенными пунктами одного из районов республики Башкортостан, число транспортных средств — число автобусов, использующихся для подвоза/развоза учеников в одной из школ данного района.
Таким образом, поставка задачи принимает следующий вид.
Имеется один пункт отправлением — 0-й пункт, 24 остановки — близлежащие деревни, в которые нужно развозить учеников, 12 автобусов вместимостью 22 человека. Дороги характеризуются одним параметром — расстоянием и являются двусторонними. Автобусы не должны возвращаться на пункт отправления. Требуется найти такой набор маршрутов, чтобы развезти всех учеников по остановкам, при этом минимизировать расстояние, которое проезжает автобус для высадки ученика на последней остановке самого длинного маршрута.
5.2. Исходные данные
Дано:
Школа — пункт отправления;
S = 24 — количество остановок (близлежащих деревень);
Обозначения школы и соседних деревень представлены в таблице 3.1.
R = 12 — количество автобусов;
Q = 22 — вместимость автобусов;
R*Q = 264 — количество учеников;
В таблице 1 представлено решение задачи — расстояние и маршрут каждого автобуса. В скобках указано число учеников, высаженных в различных пунктах назначения.
Таблица 1
Решение задачи
|
№ Автобуса |
Маршрут |
Длина маршрута, км |
|
1 |
0–11(2) — 22(20) |
42,7 |
|
2 |
0–18(15) — 19(7) |
38,1 |
|
3 |
0–17(18) — 23(4) |
37,7 |
|
4 |
0–15(3) — 20(19) |
34,1 |
|
5 |
0–1(14) — 3(2) — 11(6) |
31,8 |
|
6 |
0–10(5) — 17(1) — 21(2) |
31,3 |
|
7 |
0–1(4)– 3(0)– 12(11) |
30 |
|
8 |
0–15(1)– 16(21) |
27,4 |
|
9 |
0–5(4) — 8(5)– 5(0)– 9(12) |
35,5 |
|
10 |
0–13 (3)– 0–2 (11)– 7 (11) |
41,2 |
|
11 |
0–6 (8) — 0–13 (3) — 14 (19) |
41,1 |
|
12 |
0–2(10)– 4(1) — 0–6(9)– 24 (13) |
43,1 |
Время, потраченное разработанным ПП на поиск решения, равно 0.00 сек.
6. Анализ полученных результатов
Как видно по таблице 1 самый длинный путь[2] — это путь 0–11–22 равный 42,7 км. Это маршрут автобуса № 1.
Согласно применяемому способу решения, самый длинный маршрут не может быть меньше 42,7 км. Самым длинным маршрутом в полученном решении является маршрут автобуса № 12, он равен 43,1 км и является суммой длин двух маршрутов.
Так как целью задачи является минимизация длины максимального маршрута, то можно сделать вывод, что алгоритм работает хорошо — даже когда автобусу необходимо совершить повторный рейс, общее расстояние, которое он проезжает не намного больше самого длинного пути. В рассматриваемом примере разница между этими величинами равна всего 0,4 км.
7. Вычислительная эффективность
Время работы ПП в зависимости от числа переменных представлено в таблице 2 Как видно по нижеприведенным данным, решение задачи находится очень быстро.
Программа работает для задач, в условиях которых не более 52 остановок.
Таблица 2
Время работы программы в зависимости от числа переменных
|
№ |
Число остановок |
Количество автобусов |
Вместимость автобусов |
Время поиска решения, сек. |
|
1. |
8 |
8 |
15 |
0.00 |
|
2. |
9 |
4 |
20 |
0.00 |
|
3. |
20 |
5 |
14 |
0.05 |
|
4. |
30 |
8 |
25 |
0.05 |
|
5. |
40 |
12 |
25 |
0.05 |
|
6. |
45 |
17 |
35 |
0.05 |
|
7. |
50 |
15 |
30 |
0.05 |
|
8. |
52 |
18 |
36 |
0.05 |
Литература:
1. Newton, R.M., Thomas, W.H., 1969. Design of school bus routes by computer. Socio-Economic Planning Sciences 3 (1), 75–85.
2. Li, L., Fu, Z., 2002. The school bus routing problem: a case study. Journal of the Operational Research Society 53, 552–558.
3. Desrosiers, J., Ferland, J.A., Rousseau, J.-M., Lapalme, G., Chapleau, L., 1981. An overview of a school busing system. In: Jaiswal, N.K. (Ed.), Scientific Management of Transport Systems. North-Holland, Amsterdam, pp. 235–243.
4. Toth, P., Vigo, D., 2002. The Vehicle Routing Problem. SIAM, Philadelphia, PA.
5. Min, H., Jayaraman, V., Srivastava, R., 1998. Combined location-routing problems: a synthesis and future research directions. European Journal of Operational Research 108 (1), 1–15.
6. Bektas, T., Elmastas, S., 2007. Solving school bus routing problems through integer programming. Journal of the Operational Research Society 58 (12), 1599–1604.
7. Бронштейн Е. М., Гиндуллин Р. В. Об одном классе задач маршрутизации”// Матем. моделирование, 23:6 (2011), 123–132
8. Емельянова Т. С. Эвристические и метаэвристические методы решения динамической транспортной задачи.
9. http://www.ise.ncsu.edu/fangroup/ie789.dir/IE789F_tabu.pdf
10. http://bashkiria-map.ru/849809.html
11. http://ru.wikipedia.org/wiki/Алгоритм_Дейкстры







