Пусть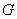 
– простая односвязная алгебраическая группа над алгебраически замкнутым полем 
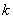характеристики 
, 
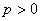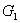– ядро отображения Фробениуса для 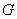и 
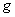– алгебра Ли группы 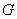. В категории ограниченных модулей теория представлений 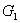и теория представлений алгебры Ли 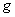эквивалентны [1; часть I, п. 9.6]. Следовательно, когомология ограниченного модуля для 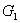и соответствующая ограниченная когомология алгебры Ли 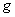также эквивалентны. Ограниченная когомология ограниченной алгебры Ли для ограниченного модуля была введена Хохшильдом в [2]. В этой же работе была построена точная последовательность, устанавливающая связь между ограниченной и обычной когомологиями алгебры Ли, а также изучены свойства начальных членов этой последовательности. В частности, установлено эквивалентность первой обычной и первой ограниченной когомологий ограниченной алгебры Ли. Для второй когомологии это утверждение же неверно. Однако известные примеры классических алгебр Ли малых рангов показывают, что в этих случаях вторые ограниченные и обычные когомологий простых ограниченных нетривиальных модулей совпадают. В данной работе доказывается, что, если соответствующая первая группа когомологии тривиальна, то последнее утверждение распространяется для всех классических алгебр Ли над алгебраически замкнутым полем положительной характеристики.
Теорема 1. Пусть 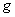– классическая алгебра Ли над алгебраически замкнутым полем 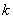характеристики 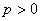. Предположим, что для алгебры Ли типа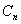 
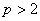. Если 
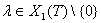и 
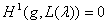, то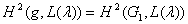 
.
Доказательство. Для всех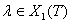 
справедлива следующая точная последовательность Хохшильда:
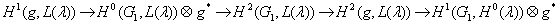. (1)
Если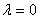 
и все условия теоремы 1 выполнены, то 
, 
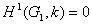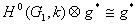и из точной последовательности (1) получаем следующую короткую точную последовательность 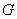-модулей:
.
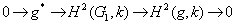Все нетривиальные случаи когомологии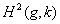 
подробно изучены в работах [3], [4].
Если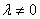 
и все условия теоремы 1 выполнены, то очевидно, что 
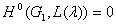и из точности последовательности (1) следует требуемый изоморфизм теоремы 1. Доказательство теоремы 1 завершено.
Если , то вероятнее всего утверждение теоремы 1 также выполняется, но доказать это пока не удается. Для когомологии индуцированного модуля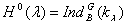 
в работах [5], [6] получена следующая замечательная формула, справедливая для 
,
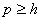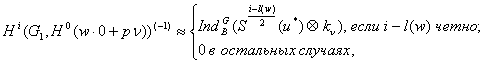(2)
где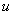 
– максимальная нильпотентная подалгебра алгебры Ли группы 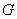, соответствующая отрицательным корням, 
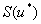– симметрическая алгебра на 
, 
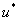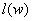– длина элемента 
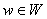. Формальных характеров 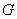-модуля 
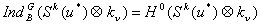можно вычислить по формуле
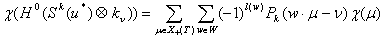, (3)
где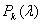 
– размерность 
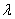-весового подпространства пространства 
.
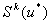Для вычисления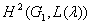 
, где 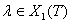, можно использовать следующий алгоритм:
1) Вычислить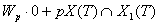 
.
2) Если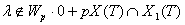 
, то по принципу связанности для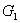 
.
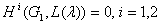3) Пусть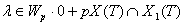 
. Отношение сильной связанности, введенное Андерсеном в [7], является отношением эквивалентности на множестве 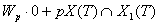и делит это множество на эквивалентные классы, сильно связанных с друг другом элементов. Число эквивалентных классов равно порядку 
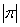фундаментальной группы 
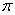системы корней 
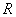. Согласно [7], элементов каждого эквивалентного класса можно упорядочить по обычному частичному порядку. Так как эквивалентные классы не пересекаются, то 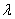принадлежит только одному из этих классов, т.е. 
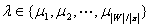. Предположим, что он упорядочен по возрастанию и 
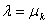для некоторого 
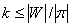. Рассматривая длинные точные когомологические последовательности 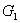-когомологии, соответствующие коротким точным последовательностям
,
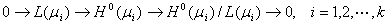и используя общую формулу Андерсена-Янцена (2), формулу формальных характеров (3), индуктивно 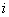по 
и по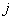 
можно вычислить когомологии 
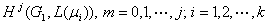. Тогда 
.
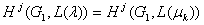Литература:
1. J.C. Jantzen. Representations of algebraic groups. – Boston: Pure and Applied Mathematics, Vol. 131. - 1987. - 446 p.
2. G. Hochschild. Cohomology of restricted Lie algebras // Amer. J. Math. - 1954. - Vol. 76. - P. 555-580.
3. W.L.J. van der Kallen. Infinitesimally central extensions of Chevalley groups, Berlin, Heidelberg, New York: Springer-Verlag, 1973.
4. Ш.Ш. Ибраев. О центральных расширениях классических алгебр Ли // Сиб. электрон. матем. изв. – 2013. – Т. 10. – С. 450-453.
5. Andersen H.H., Jantzen J.C. Cohomology of induced representations for algebraic groups // Math. Annal. - 1984. - Vol. 269. - P. 487-525.
6. Kumar S., Lauritzen N., Thomsen J. Frobenius splitting of cotangent bundles of flag varieties // Invent. Math. - 1999. - Vol. 136. - P.603-621.
7. Andersen H.H. The strong linkage principle // J. Reine Anew. Math. - 1980. - Vol. 315. - P. 53-59.
