Пусть 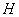 комплексное гильбертово пространство и
комплексное гильбертово пространство и 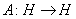 линейный оператор с областью определения
линейный оператор с областью определения 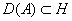 . Множество
. Множество
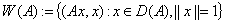 .
.
называется числовым образом оператора  . Из определения видно, что множество
. Из определения видно, что множество 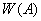 является подмножеством комплексной плоскости и геометрические свойства множества
является подмножеством комплексной плоскости и геометрические свойства множества 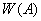 дает некоторые информации об операторе
дает некоторые информации об операторе  .
.
Изучение числового образа линейного оператора в гильбертовом пространстве является одним из основных методов в изучении местоположения спектра таких операторов. Это понятие впервые введено в работе [1] и доказано, что числовой образ матрицы содержит все ее собственные значения. В работе [2] показано, что числовой образ оператора является выпуклым. Отметим, что выше сказанные результаты верны не только для матриц, но и в более общем случае для любого линейного ограниченного оператора. В работе [3] доказано, что спектр любого линейного ограниченного оператора содержится в замыкании числового образа этого оператора. Вслед за этим это понятие обобщено разными способами, см. например [4–7].
В данной работе рассматривается линейный ограниченный самосопряженный модель Фридрихса с одномерным возмущением. Найден явный вид числового образа этого оператора.
Для полноты сначала приведем ряд основных свойств числового образа линейного оператора (вообще говоря несамосопряженного) 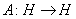 , доказательство которых вытекает непосредственно из определения. Обозначим через
, доказательство которых вытекает непосредственно из определения. Обозначим через  и
и 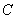 — множество всех вещественных и комплексных чисел, соответственно. Всюду в работе под
— множество всех вещественных и комплексных чисел, соответственно. Всюду в работе под 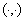 и
и 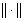 понимается скалярное произведение и норма в соответствующих гильбертовых пространствах.
понимается скалярное произведение и норма в соответствующих гильбертовых пространствах.
1) Если  ограниченный оператор, то
ограниченный оператор, то 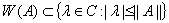 ;
;
2) 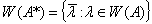 ;
;
3) 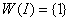 . Если
. Если  и
и  произвольные комплексные числа, то имеет место
произвольные комплексные числа, то имеет место
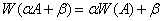 ;
;
4) Для самосопряженного оператора  имеет место соотношение
имеет место соотношение 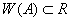 ;
;
5) Если 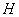 конечномерное пространство, то множества
конечномерное пространство, то множества 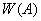 является компактным;
является компактным;
6) Если 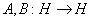 унитарно эквивалентные операторы, то
унитарно эквивалентные операторы, то 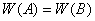 ;
;
7) 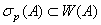 , где
, где 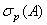 точечный спектр оператора
точечный спектр оператора  ;
;
Определим (см. [8]) аппроксимативно точечный спектр линейного оператора  как
как
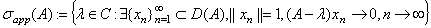 .
.
Подчеркнем, что последнее множество имеет еще одно название, «ядро спектра» оператора  (см. [9]).
(см. [9]).
Следующее утверждение устанавливает связь между 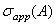 и
и 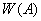 :
:
8) 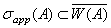 .
.
Теперь перейдем к постановку задачи и обсуждение основного результата.
Пусть 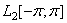 — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 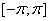 .
.
Рассмотрим модель Фридрихса  действующего в гильбертовом пространстве
действующего в гильбертовом пространстве 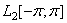 по формуле
по формуле
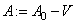 ,
,
где операторы 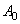 и
и 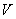 определяются равенствами
определяются равенствами
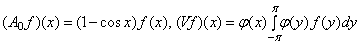 .
.
Здесь 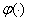 — вешественнозначная непрерывная функция на
— вешественнозначная непрерывная функция на 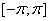 .
.
Можно проверить, что при этих предположениях оператор  является ограниченным и самосопряженным в гильбертовом пространстве
является ограниченным и самосопряженным в гильбертовом пространстве 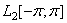 .
.
Обозначим через 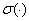 ,
, 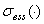 и
и 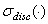 , соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
, соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Оператор возмущения 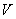 оператора
оператора 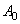 является одномерным самосопряженным оператором. Следовательно, из известной теоремы Г. Вейля [8] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора
является одномерным самосопряженным оператором. Следовательно, из известной теоремы Г. Вейля [8] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора  совпадает с существенным спектром оператора
совпадает с существенным спектром оператора 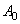 . Известно, что
. Известно, что
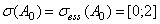 . Из последних фактов следует, что
. Из последних фактов следует, что 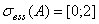 .
.
Определим регулярную в 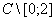 функцию (детерминант Фредгольма, ассоциированный с оператором
функцию (детерминант Фредгольма, ассоциированный с оператором  )
)
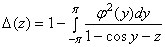 .
.
Установим связь между собственными значениями оператора  и нулями функции
и нулями функции 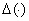 .
.
Лемма 1. Оператор  имеет собственное значение
имеет собственное значение 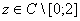 тогда и только тогда, когда
тогда и только тогда, когда 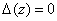 .
.
Доказательство. Пусть число 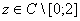 — есть собственное значение оператора
— есть собственное значение оператора  и пусть
и пусть 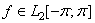 — соответствующая собственная функция. Тогда
— соответствующая собственная функция. Тогда 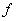 удовлетворяет уравнению
удовлетворяет уравнению 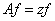 или
или
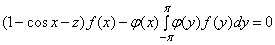 . (1)
. (1)
Для любых 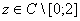 и
и 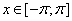 имеет место соотношение
имеет место соотношение 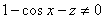 .
.
Из уравнения (1) для 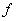 имеем
имеем
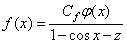 , (2)
, (2)
где
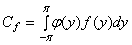 . (3)
. (3)
Подставляя выражение (2) для 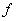 в равенство (3) получим, что уравнений (1) имеет ненулевое решение тогда и только тогда, когда
в равенство (3) получим, что уравнений (1) имеет ненулевое решение тогда и только тогда, когда 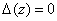 . Лемма 1 доказана.
. Лемма 1 доказана.
Согласно леммы 1 функция 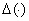 обладает характеристическим свойством определителя Фредгольма. По этой причине мы назовём её определителем Фредгольма, ассоциированный с оператором
обладает характеристическим свойством определителя Фредгольма. По этой причине мы назовём её определителем Фредгольма, ассоциированный с оператором  .
.
Из леммы 1 вытекает, что
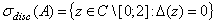 .
.
Таким образом
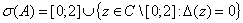 .
.
Теперь сформулируем основной результат работы.
Теорема 1. Пусть 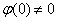 . Тогда числовой образ оператора
. Тогда числовой образ оператора  совпадает с множеством
совпадает с множеством 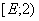 , где
, где 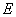 единственный простой отрицательный собственный значений оператора
единственный простой отрицательный собственный значений оператора  .
.
Доказательство. Сначала отметим, что функция 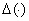 дифференцируема в полуосях
дифференцируема в полуосях 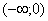 и
и 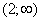 , и для любого
, и для любого 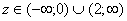 имеет место соотношение
имеет место соотношение
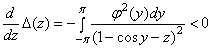 .
.
Следовательно, функция 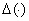 монотонна убывает в полуосях
монотонна убывает в полуосях 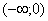 и
и 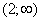 . Так как
. Так как 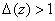 при всех
при всех 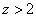 , в силу леммы 1 оператор
, в силу леммы 1 оператор  не имеет собственных значений в
не имеет собственных значений в 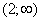 . Исследуем отрицательных собственных значений оператора
. Исследуем отрицательных собственных значений оператора  .
.
Из разложения
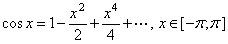
вытекает, что существуют положительные числа 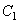 и
и 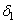 такие, что
такие, что
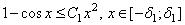 .
.
Так как непрерывная функция 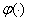 удовлетворяет условию
удовлетворяет условию 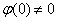 , существуют положительные числа
, существуют положительные числа 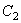 и
и 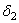 такие, что
такие, что
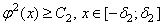 .
.
Тогда пологая 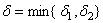 имеем, что
имеем, что
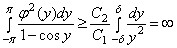 .
.
Следовательно,
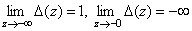 .
.
Так как функция 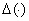 монотонно убывает в
монотонно убывает в 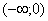 , последнее означает, что функция
, последнее означает, что функция 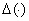 имеет единственный простой отрицательной нуль
имеет единственный простой отрицательной нуль 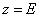 . В силу леммы 1 число
. В силу леммы 1 число 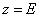 является собственным значением оператора
является собственным значением оператора  .
.
Пусть 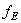 нормированная собственная функция оператора
нормированная собственная функция оператора  соответствующего собственному значению
соответствующего собственному значению 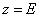 . Тогда
. Тогда
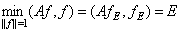 ,
,
т. е. 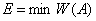 .
.
Ясно, что 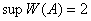 . Покажем, что
. Покажем, что 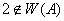 . Допустим противное. Пусть
. Допустим противное. Пусть 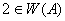 . Тогда существует функция
. Тогда существует функция 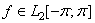 такое, что
такое, что 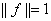 и
и 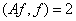 . В этом случае имеем, что
. В этом случае имеем, что
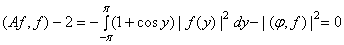 .
.
Последнее равенство выполняется тогда и только тогда, когда 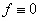 . Это противоречить условия нормировки функции
. Это противоречить условия нормировки функции 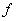 . Значить
. Значить 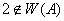 . Теорема 1 доказана.
. Теорема 1 доказана.
В ходе доказательство теоремы 1 доказано, что 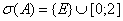 , где
, где 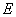 — единственной простой отрицательной собственной значение оператора
— единственной простой отрицательной собственной значение оператора  , и
, и 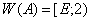 . Поэтому
. Поэтому 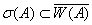 , но
, но 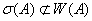
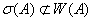 и
и 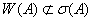 .
.
Литература:
1. O. Toeplitz. Das algebraische Analogon zu einem Satze von Fejer // Math. Z., 2:1–2 (1918), 187–197.
2. F. Hausdorff. Der Wertvorrat einer Bilinearform // Math. Z., 3:1 (1919), 314–316.
3. A. Wintner. Zur Theorie der beschrankten Bilinearformen // Math. Z., 30:1 (1929), 228–281.
4. H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range // Linear Algebra Appl., 330:1–3 (2001), 89–112.
5. L. Rodman, I. M. Spitkovsky. Ratio numerical ranges of operators // Integr. Equ. Oper. Theory, 71 (2011), 245–257.
6. M. T. Heydari. Numerical range and compact convex sets // Rend. Circ. Mat. Palermo, 60 (2011), 139–143.
7. W.-S. Cheung, X. Liu, T.-Y. Tam. Multiplicities, boundary points and joint numerical ranges // Operators and Matrices. 5:1 (2011), 41–52.
8. М. Рид, Б. Саймон. Методы современной математической физики. Т.4. Анализ операторов, М.: Мир. 1982, 430 с.
9. М. Саломяк, М. Бирман. Спектральная теория самосопряженных операторов в гильбертовом пространстве, Изд. Ленинградского университета, Ленинград, 1980, 264 c.







