Аннотация: Рассматривается задача решения уравнения колебаний балки при шарнирном закреплении границ с произвольной правой частью. Решение находится с помощью метода Фурье и проверяется сходимость полученного бесконечного ряда. Также численно строится решение на компьютере с оцениванием минимального количества членов ряда, которые нужно взять.
Ключевые слова: уравнение колебаний балки, шарнирное закрепление, метод Фурье, формулы Филона.
Постановка задачи. Колебания балки описываются следующим уравнением
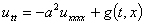 ,
, 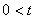 ,
,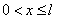 ,
,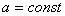 (1)
(1)
Начальные отклонения и скорость перемещения балки
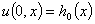 ,
, 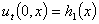 , (2)
, (2)
будем рассматривать как начальные условия. На концах балки наложим условия нежёсткого закрепления
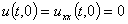 ,
, 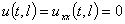 . (3)
. (3)
Функция 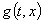 будет из пространства
будет из пространства 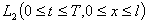 и может носить произвольный характер, но чаще всего её удобнее задавать как произведение двух функций
и может носить произвольный характер, но чаще всего её удобнее задавать как произведение двух функций 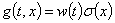 , где
, где 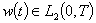 , а
, а 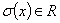 . Но для наших целей будем считать её произвольной.
. Но для наших целей будем считать её произвольной.
Необходимо найти решение уравнения (1), то есть выразить функцию 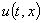 .
.
Аналитическое решение. Рассмотрим задачу (1) – (3) и будем искать решение этой задачи в виде
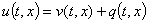 (4)
(4)
где 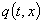 – решение задачи
– решение задачи
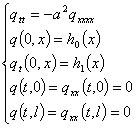 (5)
(5)
а 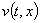 – решение задачи
– решение задачи
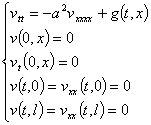 . (6)
. (6)
Для решения задачи (5) воспользуемся методом Фурье [1-4], т.е. будем искать (не равное тождественному нулю) частное решение уравнения задачи (5), удовлетворяющее граничным условиям этой задачи, в виде произведения двух функций 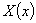 и
и 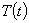 , из которых первая зависит только от переменной
, из которых первая зависит только от переменной 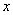 , а вторая только от переменной
, а вторая только от переменной 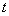 :
:
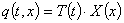 (7)
(7)
Подставляя (7) в уравнение задачи (5) получаем соотношение:
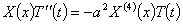 (8)
(8)
и, разделив члены равенства на 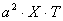 , получим
, получим
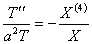 . (9)
. (9)
В левой части равенства (9) стоит функция, которая не зависит от переменной 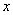 , справа – функция, не зависящая от переменной
, справа – функция, не зависящая от переменной 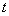 . Это равенство возможно только в том случае, когда левая и правая части (9) не зависят ни от переменной
. Это равенство возможно только в том случае, когда левая и правая части (9) не зависят ни от переменной 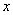 , ни от переменной
, ни от переменной 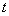 , то есть равны постоянному числу. Обозначим это число через константу
, то есть равны постоянному числу. Обозначим это число через константу 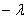 ,
, 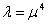
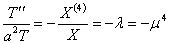 (10)
(10)
Соотношение (10) даёт нам два ниже следующих уравнения
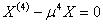 (11)
(11)
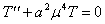 (12)
(12)
Характеристическое уравнение для (11) имеет следующий вид
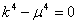 (13)
(13)
Решая его, получим 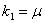 ,
, 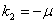 ,
, 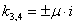 . Следовательно, решением уравнения (11) будет функция
. Следовательно, решением уравнения (11) будет функция
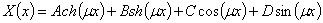 , (14)
, (14)
где 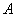 ,
, 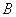 ,
, 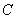 ,
, 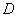 – произвольные постоянные числа.
– произвольные постоянные числа.
Из первых двух краевых условий задачи (5) получаем, что 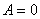 и
и 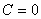 . Из вторых двух условий образуется система
. Из вторых двух условий образуется система
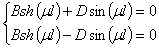 . (15)
. (15)
У этой системы имеется нетривиальное решение, если её детерминант равен нулю
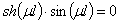 (16)
(16)
Равенство 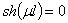 выполняется только тогда, когда выполняется следующее равенство
выполняется только тогда, когда выполняется следующее равенство 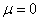 . Но при
. Но при 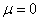 получается, что
получается, что 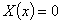 . Этот случай нам не интересен, поэтому пусть
. Этот случай нам не интересен, поэтому пусть 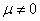 . Тогда
. Тогда 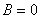 , а из
, а из 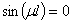 следует, что собственные значения равны
следует, что собственные значения равны
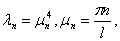
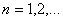 , (17)
, (17)
В результате получаем собственные функции, соответствующие собственным значениям,
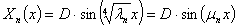 (18)
(18)
Решение уравнения (12) имеет вид
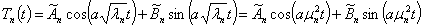 (19)
(19)
Тогда, по методу Фурье, получаем следующее выражение для функции 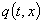 задачи (5)
задачи (5)
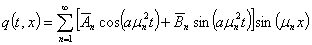 (20)
(20)
Подставляя (20) в начальные условия задачи (5), получаем
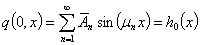 (21)
(21)
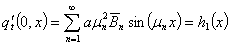 (22)
(22)
Тогда коэффициенты ряда Фурье принимают следующий вид
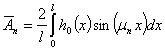 (23)
(23)
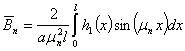 (24)
(24)
Рассмотрим задачу (6). Разложим функцию 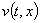 и
и 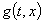 по собственным функциям (18)
по собственным функциям (18)
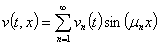 (25)
(25)
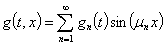 (26)
(26)
Подставляя (25) и (26) в уравнение задачи (6) получим
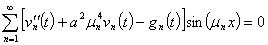 (27)
(27)
Из (27) получается следующее равенство
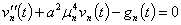 (28)
(28)
После подстановки функции (25) в начальные условия задачи (6) условия для (28) принимают следующий вид
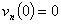 (29)
(29)
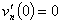 (30)
(30)
Рассмотрим однородное
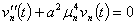 . (31)
. (31)
Его решением является следующая функция
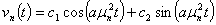 . (32)
. (32)
Воспользуемся методом вариации постоянной
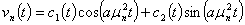 . (33)
. (33)
Выражение (33) будем использовать для определения общего решения уравнения (28), для этого вычислим следующие выражения
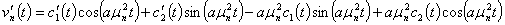 (34)
(34)
и пусть 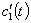 и
и 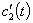 будут такими, что
будут такими, что
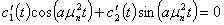 , (35)
, (35)
тогда
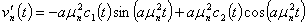 (36)
(36)
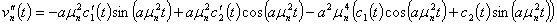 (37)
(37)
Подставив (33) и (37) в (28) получим следующее уравнение
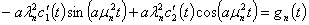 . (38)
. (38)
Для определения 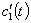 и
и 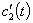 будем решать систему (35), (38), откуда получаем
будем решать систему (35), (38), откуда получаем
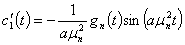 (39)
(39)
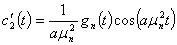 . (40)
. (40)
Следовательно, проинтегрировав, получим
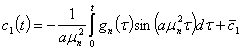 , (41)
, (41)
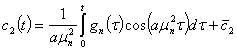 . (42)
. (42)
Тогда общее решение уравнения (28) примет вид
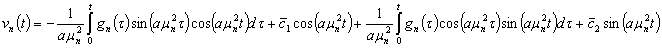 или
или
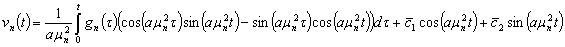 (43)
(43)
откуда окончательно получаем
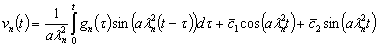 (44)
(44)
Задача Коши (28) – (30) имеет решение
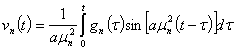 (45)
(45)
Следовательно, общее решение задачи (6) можно записать в следующем виде
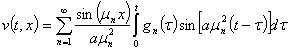 , (46)
, (46)
где 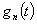 получается по формуле коэффициентов ряда Фурье
получается по формуле коэффициентов ряда Фурье
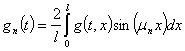 . (47)
. (47)
Таким образом, общее аналитическое решение задачи (1) – (3) имеет вид
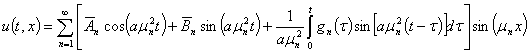 (48)
(48)
Проверим, что полученный ряд в действительности является решением.
Проверка сходимости решения. Для того чтобы проверить, что ряд (48) действительно является решением, необходимо показать, что он сходится. В случае, если он сходится, мы можем с точность утверждать, что он сходится к конкретной функции, которая и является решением уравнения колебаний балки. И так, мы нашли общий вид решения (48) и соответствующие коэффициенты Фурье (23), (24) и (47)
Чтобы показать, что ряд (48) сходится, необходимо, чтобы сходились три ряда, входящие в его сумму [3, 4], а именно
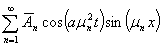 (49)
(49)
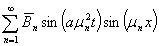 (50)
(50)
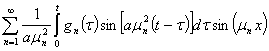 (51)
(51)
Ряд (51) сходится в силу следующей оценки общего члена ряда
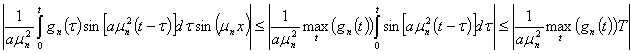
А ряд, полученный в результате этой оценки,
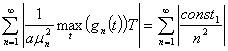 (52)
(52)
является сходящимся. Поэтому ряд (51) сходится. Произведём оценку общего члена ряда (50), в результате получаем следующее
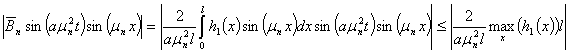
А ряд, полученный в результате этой оценки,
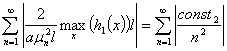 (53)
(53)
является сходящимся. Поэтому ряд (50) сходится. Произведём оценку общего члена ряда (49), в результате получаем следующее
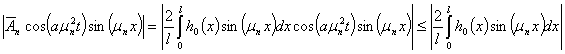
Тогда сходимость ряда (49) становится задачей исследования сходимости ряда
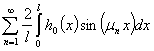 (54)
(54)
Воспользуемся формулой интегрирования по частям два раза. В первый раз получится
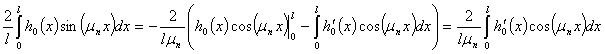
Во второй раз получится следующее выражение
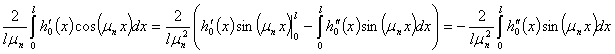
При этом ряд, составленный из последнего выражения можно оценить так
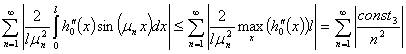 (55)
(55)
Ряд (55) является сходящимся, поэтому ряд (49) сходится. А так как все три ряда (49), (50), (51), входящие в сумму ряда (48), сходятся, то и ряд (48) сходится.
Лемма. Для того чтобы ряд (48) был сходящимся необходимо, чтобы начальное условие 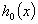 было дважды дифференцируемо.
было дважды дифференцируемо.
Построение полученного решения на компьютере. Для того чтобы графически построить решение уравнения колебаний будут использоваться следующие подходы.
Во-первых, для удобства и наглядности будет использоваться решение однородного уравнения (1), то есть решение вида
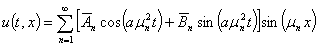 (56)
(56)
Во-вторых, необходимо оценить примерное количество членов ряда, которые необходимо взять, чтобы построить решение с заданной точностью 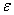 . Для этого можно попробуем оценить ряд (56) как есть, тогда, подставляя в него значения коэффициентов Фурье, получаем
. Для этого можно попробуем оценить ряд (56) как есть, тогда, подставляя в него значения коэффициентов Фурье, получаем
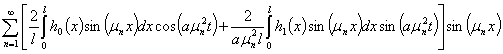
Рассмотрим частичную сумму
Следовательно, нам необходимо найти такой номер 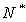 , начиная с которого частичные суммы выстраивались бы в последовательность Коши
, начиная с которого частичные суммы выстраивались бы в последовательность Коши
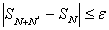
От сюда следует, что мы ищем 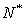 из следующего неравенства
из следующего неравенства
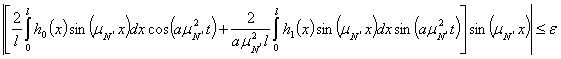
Это выражение можно оценить следующим образом
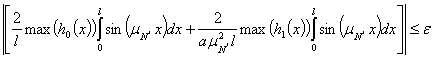
Тогда имеет место следующая запись
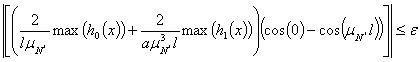
Чтобы это выражение имело смысл, необходимо, чтобы 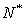 не было кратным двум. Тогда
не было кратным двум. Тогда
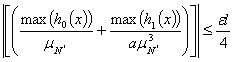 и, соответственно,
и, соответственно, 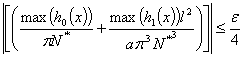
Согласно известному неравенству [3,4] можно получить следующее
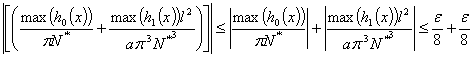
Второй ряд в сумме сходится быстрее, чем первый, поэтому нам достаточно оценить первый из них. Получим оценку на общий член ряда, тогда можно записать
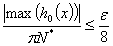 , или
, или 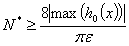 (57)
(57)
Пример №1. Для примера возьмём следующие начальные условия 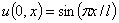 ,
, 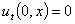 ,
, 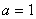 , тогда при длине балки
, тогда при длине балки 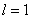 и желаемой точности
и желаемой точности 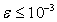 получаем, что минимальное количество членов ряда должно равняться
получаем, что минимальное количество членов ряда должно равняться
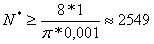 .
.
В-третьих, косинусы и синусы являются быстро осциллирующими функциями. Поэтому необходимо воспользоваться подходом Филона [5] для численной работы с ними. Для этого введём равномерную сетку [5] узлов интегрирования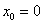 ,
, 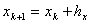
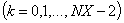 , так чтобы
, так чтобы 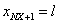 , и где
, и где 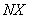 – кол-во точек по оси
– кол-во точек по оси 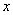 , вычисляемое как
, вычисляемое как 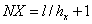 . Запишем интегралы (23) и (24) следующим образом
. Запишем интегралы (23) и (24) следующим образом
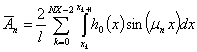 , (58)
, (58)
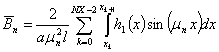 , (59)
, (59)
Теперь воспользуемся подходом Филона и получим квадратурные формулы типа прямоугольника (Филона-А)
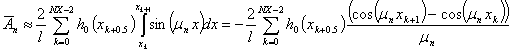
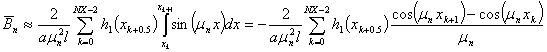
Или, воспользовавшись формулами тригонометрии, можно написать
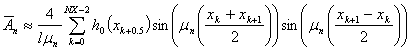 (60)
(60)
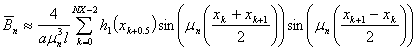 (61)
(61)
Окончательно можно записать так
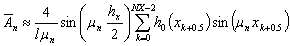 (62)
(62)
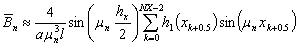 (63)
(63)
Пример №2. Построим графически решение (56) однородного уравнения колебаний балки (1) на примере условия примера №1: 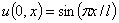 ,
, 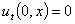 ,
, 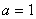 ,
, 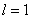 , для времени
, для времени 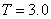 . Тогда количество членов ряда будет 2549 (см. Пример №1), а интегралы (23) и (24) будут рассчитываться по формулам (62) и (63), при этом
. Тогда количество членов ряда будет 2549 (см. Пример №1), а интегралы (23) и (24) будут рассчитываться по формулам (62) и (63), при этом 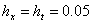 .
.
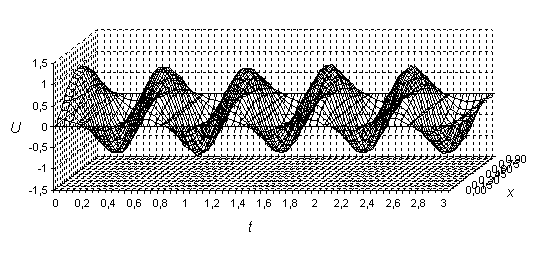
Рис 1. Свободные колебания балки.
Программа, реализующая построение решения, была создана на C/C++.
Литература:
Владимиров В.С., Жаринов В.В. Уравнения математической физики. Москва: ФЗМАТЛИТ, 2004. 400 с.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. Москва: Наука, 1977. 736 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 1. Москва: Наука, 1968. 552 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 2. Москва: Наука, 1968. 312 с.
Косарев В.И. 12 лекций по вычислительной математике (вводный курс). Москва: МФТИ, 2000. 224 с.







