Пусть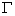 
— замкнутая Жорданова спрямляемая кривая, 
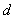- диаметр , 
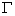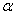- сохраняющий ориентацию гомеоморфизм (сдвиг) 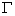на себя имеющий непустое множество 
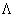периодических точек.
В соответствии с [1] в качестве характеристики контура 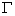и непрерывных на 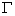функций введем следующие функции
.
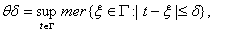
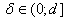
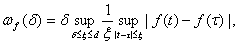
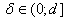В дальнейшем предполагается, что
.
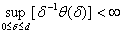Обозначим через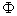 
класс неотрицательных функций 
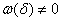заданных в промежутке 
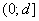и удовлетворяющих условиям (см., например, [2]):
a)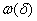 
является модулем непрерывности
b)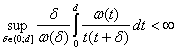 
Каждой функции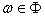 
сопоставляется обобщенное пространство Гёльдера 
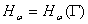, состоящее из комплексных непрерывных на 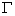функции 
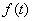с конечной нормой
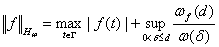
Очевидно,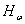 
- Банахова алгебра.
Предположим, что сдвиг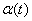 
удовлетворяет условия: функция
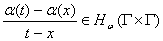определена на 
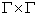и отлична от нуля. Как известно (см. например, [3]. с 24), точки 
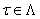имеют одинаковые периоды 
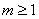. Кроме того, при данных условиях функция 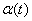дифференцируема, ее производная 
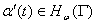и 
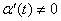для всех 
.
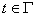В пространстве 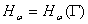, , 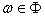рассмотрим оператор
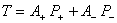(1)
где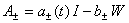 
, функции 
, 
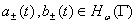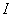- тождественный оператор, 
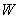- оператор сдвига: 
, 
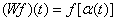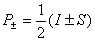
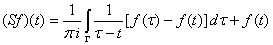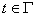, . (2)
В работе используются следующие обозначения: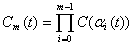 
, где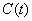 
- непрерывная функция в , 
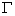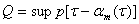— замыкание множества всех точек 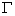, в которых 
;
; 
; 
;
; 
;
; 
; 
;
; 
;
;
.
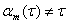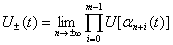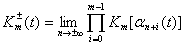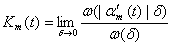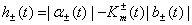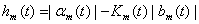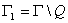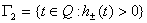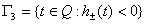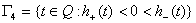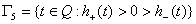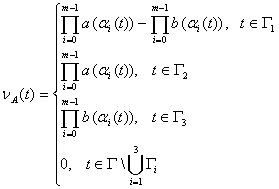
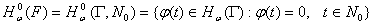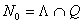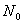- может быть бесконечное, конечное и пустое множество. Отметим, что в периодических точках 
.
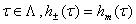В работе ([4]) получен критерий односторонней обратимости оператора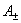 
в пространствах 
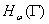и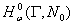 
. В данной работе устанавливаются критерии 
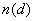- нормальности операторов 
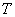в пространствах 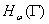. (Оператор 
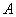называется 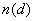- нормальным, если его образ замкнут и конечномерны ядро (коядро)). Отметим, что оператор([6].c 195)
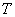
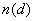- нормален тогда и только тогда, когда 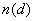- нормалны операторы 
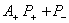и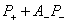 
. Таким образом, достаточно доказать теоремы для оператора 
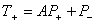, где 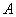- оператор имеет вид 
, 
.
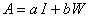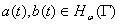Теорема 1. Оператор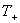 
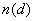- нормален в пространстве 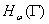тогда и только тогда, когда оператор 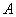обратим слева (справа) в 
.
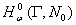Доказательство теоремы опирается на следующие леммы.
Лемма 1. Если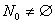 
, то оператор 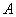обратим слева (справа) в пространстве 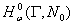тогда и только тогда, когда оператор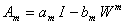 
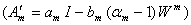- обратим слева (справа) в пространстве 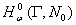и выполняются условия
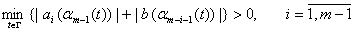
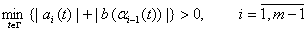
Лемма 2. Если 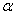являются сдвигом Карлемана, то есть 
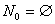, то оператор 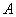односторонне обратим в пространстве 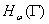тогда и только тогда, когда оператор 
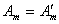обратим в 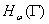, т. е. 
, 
.
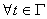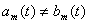Доказательств этих двух лемм аналогично доказательству соответственно леммы 10.2 и леммы 10.3 работу [6].
Доказательство теоремы. Достаточность. Доказательство проведем для случая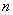 
-нормальности оператора 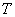.(случай 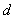-нормальности рассматривается аналогично)
Пусть оператор 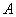обратим слева в 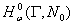.Тогда согласно лемме 1 и лемме 2 выполняется условие 
, 
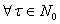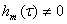. Следовательно, обратимость слева 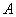в 
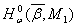где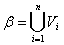 
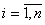конечное покрытие множеств 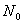, концы которых лежат в , 
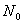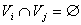при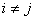 
, 
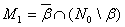, эквивалентна обратимости слева 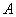в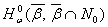 
. С другой стороны легко заметить, что 
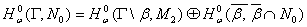где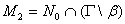 
и пространства 
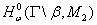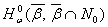и являются инвариантными относительно оператора .
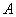Так как обратимость слева оператора 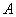в 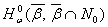эквивалентна обратимости слева 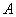в 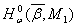, то отсюда получаем, что оператор 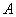обратим слева в пространстве
.
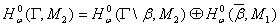В 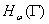определим проектор 
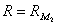формулами
, 
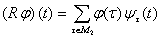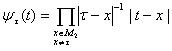
если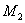 
неоднотогечно, и 
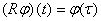, если 
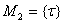. Так как 
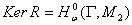то 
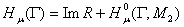. Отсюда, так как 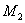-конечное множество, получаем что оператор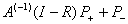 
где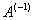 
- соответствующий обратный к 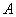в 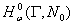, является соответствующим односторонним регуляризатором оператора 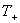. Достаточность доказано.
Необходимость доказывается аналогично доказательству теоремы 13.1. работы [6]
Из этой теоремы и из теоремы-2 в работе [4] вытекает.
Теорема 2. Оператор 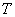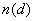-нормален в пространстве 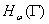, тогда и только тогда, когда 
, 
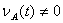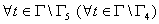
и
, 
, 
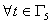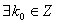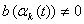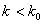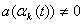при 
, 
при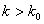 
(Соответственно,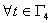 
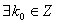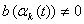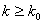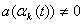, , при 
, при )).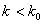
Литература:
1. А. И. Гусейнов, Х. Ш. Мухтаров Введение в теорию нелинейных сингулярных интегральных уравнений.-М.:Наука-1980
2. Б. Турсунқулов О вполне непрерывных операторах в обобщенных Гёльдеровских пространствах. Докл.АН УзССР, 1982 № 12,стр.4–6
3. Литвинчук Г. С. Краевые задачи и сингулярные интегральные уравнения со сдвигом. — М.: Наука 1977
4. Р.Мардиев, Б. М. Турсункулов, Н. А. Тошева. Об обратимости функционалных операторов со сдвигом в обобщённых пронстранствах Гёлдера. ТАТУ. Материалы научно-практической конференции. Часть II. Сам. 2013 й.
5. И.И Гохберг, Н. Я. Крупник Введение в теорию одномерных сингулярных операторов Кишинев.: Штиница 1973
6. Р.Мардиев Нормально разрешимые сингулярные интегральные операторы с некарлемановским сдвигом, имеющим непустое множество периодических точек. Дис. Канд. Физ-мат. Наука. Самарканд, 1988 г
