Пусть задана конечная строго возрастающая последовательность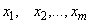 
значений 
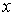, где 
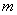— число значений — достаточно велико, и последовательность 
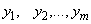соответствующих значений некоторой функции 
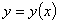. Пусть также задана допустимая погрешность 
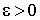равномерного приближения заданных значений этой функции некоторой гладкой функцией.
При ограниченности ресурсов и быстродействия бортовых ЭВМ особенно актуальна задача разбиения последовательности 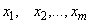на возможно более длинные последовательности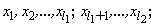 
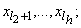
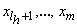(каждая из которых, за возможным исключением последней, содержала бы более трех точек), чтобы на каждой такой последовательности можно было аппроксимировать функцию 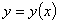по методу наименьших квадратов полиномом степени не выше третьей с допустимой погрешностью. Если же последняя последовательность содержит лишь три точки 
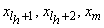, то на ней произвести параболическую интерполяцию функции 
; если лишь две точки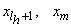 
— линейную; если лишь одну точку 
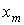— придать аппроксимирующей функции в этой точке заданное значение 
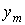аппроксимируемой функции. Выполнив эту аппроксимацию, сочленить полиномы на стыках 
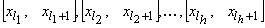гладким образом с помощью полиномов третьей степени, а если последняя последовательность содержит лишь одну точку 
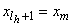то на последнем стыке 
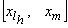сочленить полином и значение 
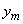в конечной точке 
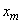гладким образом с помощью полинома второй степени. В результате будет произведена равномерная аппроксимация с допустимой погрешностью сплайном не выше третьей степени.
Приведем описание разработанного автономного программного обеспечения для гладкой аппроксимации. Оно является объединением приводимых ниже информационно-связных модулей.
1. Модуль В. Ввод данных, подготовка первого цикла.
2. Модуль А. Аппроксимация по методу наименьших квадратов полиномом степени не выше третьей с допустимой погрешностью на возможно более длинной (более трех точек) последовательности, начиная с данной точки (цикл); рис.1а.
3. Модуль И. Интерполяция на последней последовательности, если она содержит не более трех точек.
4. Модуль П. Переадресация с целью перехода от одной последовательности к другой (от одного цикла А к другому в пределах всей заданной последовательности значений независимой переменной); рис.1б.
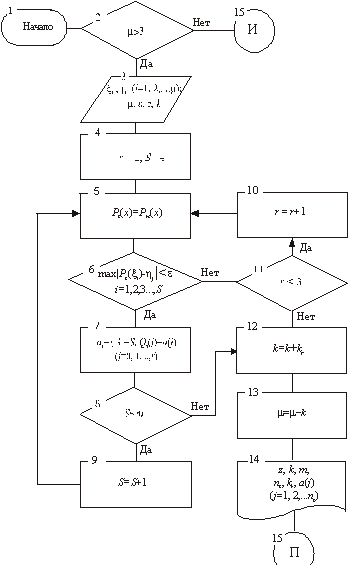
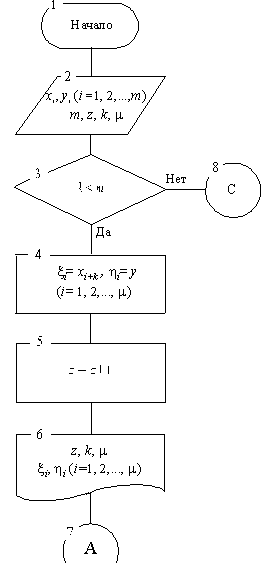
а) б)
Рис. 1. Схемы работы модулей: а) — модуль А; б) — модуль П.
1. Модуль С. Сочленение аппроксимирующей функции на стыках гладким образом полиномами третьей, а на последнем стыке, возможно, второй степени. Укажем логические схемы модулей.
Модуль В.
1) Ввод пар значений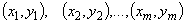 
; числа 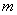этих значений 
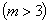; допустимой погрешности 
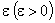равномерного приближения.
2) Передача значений в первый цикл:
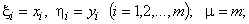
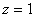(начало счета циклов);
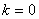(начало счета пройденных точек).
3) Переход к модулю А.
Модуль А.
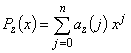— аппроксимирующий полином на 
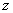— м цикле; 
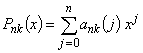- полином степени 
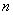, построенный методом наименьших квадратов по значениям 
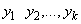функции 
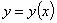в точках 
.
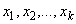Модуль И.
Пусть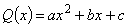 
— интерполяционный полином.
1) Ввод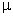
:
- если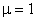 
, то вводится 
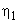и полагаем 
;
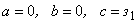- если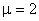 
, то вводятся 
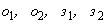и полагаем
;
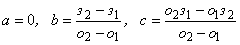- если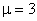 
, то вводятся 
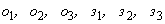и полагаем
- 
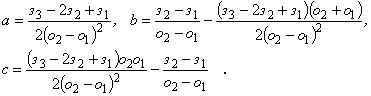
2) Выдача результатов вычислений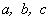 
и переход к модулю С.
Модуль С.
1) Для каждого z-го стыка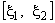 
, где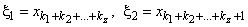 
строится сочленяющий полином 
.
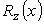При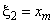 
коэффициенты 
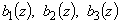полинома 
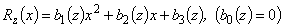находятся из системы уравнений
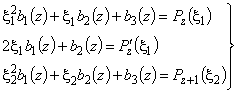
единственным образом, так как для любых различных точек определитель системы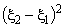 
отличен от нуля.
Аналогично при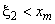 
коэффициенты 
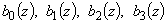полинома 
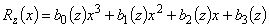также определяются единственным образом (
).
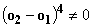2) Выдача результаты вычислений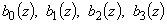 
.
Вычисления закончены.
Приведенное программное обеспечение использовалось при разработке имитаторов динамики полета [1…7].
Литература:
1. Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление: монография. — Пенза: ПГУАС, 2011. — 308 с.
2. Данилов А. М.,Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС, 2011. -296 с.
3. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. — № 5. 2013. –С.42–45.
4. Будылина Е. А., Гарькина И. А. Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. — 2013. –№ 2(16). — C. 138–143.
5. Лапшин Э. В., Данилов А. М., Гарькина И. А., Клюев Б. В., Юрков Н. К. Авиационные тренажеры модульной архитектуры: монография. — Пенза, ИИЦ ПГУ. — 2005. –146 с.
6. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы проектирования / Региональная архитектура и строительство. — 2012. — № 1. — С. 39–42.
7. Планирование эксперимента. Обработка опытных данных монография / И. А. Гарькина [и др.]; под ред. проф. А. М. Данилова.– М.: Палеотип, 2005. — 272 с.
