Исследуется проблема планирования производственной программы в условиях риска и неопределенности. Рассматривается многопродуктовая стохастическая модель оптимизации плана производства. Для формирования оптимального плана разработан алгоритм, основанный на использовании рекурсии и позволяющий ситуационно определять наилучший план производства, максимизирующий прибыль.
Ключевые слова:план производства; стохастическая оптимизационная модель производственной программы; ситуационное управление; рекурсия.
Производственная программа (план производства продукции) является важным направлением планирования на предприятии. Она разрабатывается с учетом возможностей предприятия и рыночной потребности в продукции предприятия. Расчеты производственных мощностей осуществляются техническими службами, а исследование потребностей рынка — службой маркетинга. Модели формирования производственной программы предназначены для оптимизации распределения объемов производства с учетом расходования ограниченных ресурсов. Одна из первых математических моделей была разработана в 1939 г. Л. В. Канторовичем, которая была посвящена составлению производственной программы, включающей типовые ассортиментные комплексы.
Постановка задачи определения оптимального плана производства может выполняться с различными экономическими оценками. Способ решения задачи оптимизации зависит от математического вида целевой функции и ограничений. При линейной целевой функции и ограничений методом решения будет линейной программирование, при нелинейной — возможно использование метода множителей Лагранжа или динамического программирования, при стохастических зависимостях — метод решения основан на обработке данных прошлых наблюдений и переход от стохастических параметров к их моментам первого и второго порядков, при игровой неопределенности параметров метод решения сводится к методу линейного программирования. [1–6].
Общая постановка задачи оптимизации многопродуктового производства имеет следующий вид. Предприятие выпускает n видов продукции на которые расходуется m видов ресурсов. Запас i-го ресурса составляет bi. Известны нормы расхода ресурса aij, которые показывают сколько единиц i-го вида ресурса требуется для производства единицы продукции j-го вида. Нормы расхода всех видов ресурсов в совокупности образуют технологическую матрицу производства. Прибыль от реализации j-го вида продукции равна cj. Требуется составить производственную программу, обеспечивающую предприятию максимальную прибыль. Примем искомый объем выпуска продукции j-го вида xj. Экономико-математическая модель задачи примет вид:
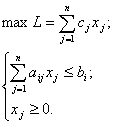
Большинство коммерческих программных продуктов и встроенных в них моделей (PIMS, RPMS, PETRO) [8–11] осуществляют планирование производства с заранее заданными условиями. То есть в процессе планирования не рассматриваются риски и неопределенность спроса, рыночной конъюнктуры, производственных параметров. Применение специальных методов управления в процессе планирования, несмотря на свою привлекательность для специалистов по планированию, представляется затруднительным, поскольку это влечет за собой совершенствование детерминированных моделей.
PIMS (Process Industry Modeling System) — система моделирования перерабатывающей промышленности) — программное решение для экономического планирования, предназначенное для моделирования промышленных процессов. PIMS позволяет оптимизировать деятельность по проектированию и дальнейшей эксплуатации нефтеперерабатывающих заводов, нефтехимических предприятий и других промышленных комплексов с использованием методов линейного программирования (с некоторой функциональной возможностью нелинейных расчетов). Для ввода и обработки исходных данных используются электронные таблицы Excel, рис. 1.

Рис. 1. Процесс формирования оптимального решения
Модели установок смоделированы как вектора база-дельта. При этом модели установок первичной переработки создаются автоматически на основе данных по сырой нефти. Свойства прямогонных продуктов «протягиваются» к пулам смешения PIMS, а также к другим подмоделям. Оптимизация проводится оптимизатором Xpress. PIMS считывает матрицу из файла, созданного генератором матриц, оптимизирует матрицу и выдает оптимальное решение. Ход решения отражается в протоколе итераций. PIMS также позволяет сохранять текущее решение в файл и использовать это решение в качестве расширенной предварительной оценки некоторого будущего варианта.
PIMS может использоваться для разнообразных целей краткосрочного и стратегического планирования, в том числе:
оценки альтернативных видов сырья;
определения размеров заводских установок при начальном проектировании;
оптимизации смеси продуктов, получаемой из конкретного набора исходных компонентов;
оптимизации смешения продуктов и других эксплуатационных решений;
анализа возможностей создания новых производств и расширения имеющихся, и многих других.
Для управления рисками в инженерных решениях уже разработано множество методик [8], использующих двухэтапное стохастическое программирование. При этом все эти методы, включая подход [8], представляют собой вычислительные проблемы. Данные методы, в случае их коммерческой реализации, потребуют внесения изменения в уже имеющийся код коммерческого программного обеспечения. С целью справиться с вычислительными проблемами, была предложена методика, которая способна к управлению риском, неоднократно используя детерминированную модель. Методика, являясь концептуально простой и практически применимой, избавляет от необходимости изменения существующего кода (добавляется только новый код).
Для решения стохастической модели определения оптимального плана производства нефтеперерабатывающего завода с использованием программы PIMS был разработан вычислительный алгоритм, позволяющий решать стохастическую задачу оптимизации в условиях риска. Целью производственной модели планирования PIMS является максимизация прибыли с учетом доходов, расходов на сырье и стоимости запасов. В качестве решения будем считать переменные, отвечающие за объем покупки сырой нефти, параметры технологических установок и внутренних потоков, объемы нефтепродуктов и запасы. Неопределенными параметрами будут: стоимость сырой нефти, спрос на продукты, цены. Данная информация является прогнозной, и для неё доступна функция плотности вероятности. Вычислительный алгоритм основан на решении двухэтапной стохастической задачи с фиксированной рекурсией и конечным числом сценариев.
Укрупнено алгоритм нахождения оптимального производственного плана состоит из следующих этапов.
1. Задание допустимого множества возможных значений плана с учетом производственной мощности и спроса.
2. Ввод целевой функции, критерия поиска и ограничений.
3. Ввод функций распределения параметров целевой функции и ограничений, оценка моментов первого и второго порядков функций распределения.
4. Определение условного экстремума целевой функции относительно ограничений с использованием рекурсивного алгоритма.
Для решения задачи стохастического программирования при планировании плана производства необходимо четко определить виды возможных рисков и неопределенностей, а также мер их количественной оценки. В статистических методах для оценки возможной величины ущерба, связанного с риском, используется функция распределения исследуемых показателей и изучаются ее моменты — математическое ожидание, среднеквадратическое отклонение, а также другие статистические характеристики такие как коэффициент вариации, квантили, комбинация математического ожидания и среднеквадратического отклонения (доверительный интервал для определения величины ущерба может быть оценен по правилу трех сигм — математическое ожидание плюс-минус три сигма), среднее значение функции потерь [7]. Если неопределенность, присущая исследуемым экономическим процессам, имеет стохастическую природу, а возможный ущерб можно описать случайной величиной, тогда задача минимизации риска сводится к одному или нескольким альтернативам: 1) минимизации среднего уровня ущерба; 2) минимизации квантиля (например, медианы функции распределения величины ущерба); 3) минимизации дисперсии; 4) минимизации линейной комбинации математического ожидания и среднеквадратического отклонения (если распределение величины ущерба близко к нормальному); 5) максимизации среднего значения функции полезности.
Реализация метода стохастического программирования для формирования оптимального плана производства с использованием коммерческого планировщика может значительно превосходить показатели прибыли, полученные с помощью детерминированных моделей.
Литература:
1. Орлова Е. В. Имитационная модель управления стохастическими финансовыми потоками предприятия // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Экономические науки. 2012. Т. 5. № 156. С. 185–189.
2. Орлова Е. В. Механизм эффективного ценообразования на продукцию промышленных предприятий // Экономика и предпринимательство. 2013. № 12–1 (41). С. 622–626.
3. Орлова Е. В. Формирование эффективной структуры затрат предприятия на основе концепции сбалансированного управления // Вестник ИНЖЭКОНа. Серия: Экономика. 2012. № 3. С. 160–166.
4. Орлова Е. В., Исмагилова Л. А. Концептуальный подход к формированию системы управления эффективностью деятельности предприятия // Аудит и финансовый анализ. 2014. № 1.
5. Орлова Е. В. Синтез оптимального управления процессом распределения стохастических финансовых потоков производственно-экономической системы // Аудит и финансовый анализ. 2013. № 6. С. 149–153.
6. Орлова Е. В. Системный анализ и моделирование экономической эффективности проектов: методический подход // Экономика и предпринимательство. 2013. № 12–4.
7. Орлова Е. В. Идентификация и прогнозирование рисков экономической системы на основе имитационного моделирования // Проблемы анализа риска. 2014. № 1.
8. Barbaro A., Bagajewicz M. Managing Financial Risk in Planning under Uncertainty // AIChE Journal. 2004. No. 50. pp. 963–989.
9. Aseeri A., Bagajewicz M. New Measures and Procedures to Manage Financial Risk with Applications to the Planning of Gas Commercialization in Asia // Computers and Chemical Engineering. 2004. Vol. 28. No. 12, pp. 2791–2821.
10. Pongsakdi A., Rangsunvigit P., Siemanond K., Bagajewicz M. Financial Risk Management in Planning of Refinery Operations // Int. J. Production Economics. 2006. No. 103. pp. 64–86.
11. Shabbir Ahmed. Two-Stage Stochastic Integer Programming: A Brief Introduction. New York: John Wiley & Sons, 2010.







