В работе изложен алгоритм одного из методов одномерной оптимизации, который называется квадратичная интерполяция или метод Пауэлла. Представлен и подробно описан код на языке php, который позволяет выполнить одномерную оптимизацию методом Пауэлла любой введенной пользователем функции.
Ключевые слова: одномерная оптимизация, квадратичная интерполяция, метод Пауэлла, квадратичная аппроксимация.
Задачи одномерной или однопараметрической оптимизации являются наиболее простыми из оптимизационных задач, но все же имеют огромную практическую и теоретическую ценность. Они часто используются в инженерной практике, а также для решения более сложных и многомерных оптимизационных задач (например, градиентный метод наискорейшего спуска использует один из методов одномерной оптимизации, за счет чего является достаточно быстрым и точным).
Задача одномерной оптимизации в общем случае заключается в поиске экстремума функции одной переменной либо в какой-то определенной окрестности, либо на всей оси абсцисс.
В основе метода Пауэлла лежит идея аппроксимирования заданной функции квадратичным полиномом. Далее покажем вывод формулы аппроксимации точки минимума некоторой функции f(x).
Если известны значения функции f(x) в трех различных точках 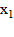 ,
, 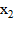 и
и 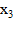 , равные соответственно
, равные соответственно 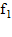 ,
, 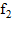 и
и 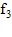 , то функция f(x) может быть аппроксимирована квадратичным полиномом g(x):
, то функция f(x) может быть аппроксимирована квадратичным полиномом g(x):
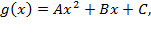 (1)
(1)
где A, B и C определяются из уравнений, найденных постановкой 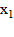 ,
, 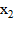 и
и 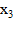 в функцию f(x),
в функцию f(x),
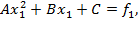 (2)
(2)
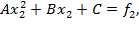 (3)
(3)
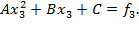 (4)
(4)
После решения системы, состоящей из уравнений (2), (3) и (4), получаем
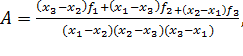 (5)
(5)
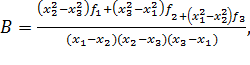 (6)
(6)
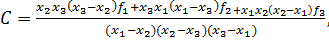 (7)
(7)
Очевидно, что функция g(x) будет иметь минимум в точке 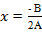 , если A>0. Значит, можно аппроксимировать точку минимума функции f(x) значением
, если A>0. Значит, можно аппроксимировать точку минимума функции f(x) значением
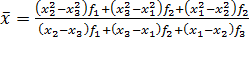 (8)
(8)
Опишем краткий алгоритм метода Пауэлла:
1. Необходимо задать начальную точку 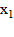 , от которой будет начинаться поиск минимума, величину шага h и точность расчетов ε.
, от которой будет начинаться поиск минимума, величину шага h и точность расчетов ε.
2. 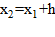
3. Вычислить 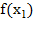 и
и 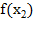 и сравнить их между собой для вычисления третьей точки
и сравнить их между собой для вычисления третьей точки 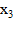 .
.
- Если 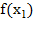 >
> 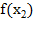 , то
, то 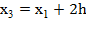 ;
;
- Если 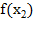 >
> 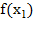 , то
, то 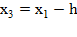 .
.
4. Вычислить 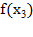 и выбрать минимальное значение
и выбрать минимальное значение 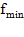 из
из 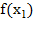 ,
, 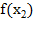 и
и 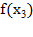 . Обозначить
. Обозначить 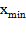 , которое находится из
, которое находится из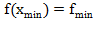 .
.
5. По формуле (8) вычислить  и
и 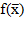 . Если знаменатель по формуле (8) равен нулю, то следует принять
. Если знаменатель по формуле (8) равен нулю, то следует принять 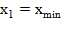 и перейти к шагу 2.
и перейти к шагу 2.
6. Проверить условие 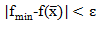 . Возможны три случая:
. Возможны три случая:
- Условие выполнено, алгоритм закончен, окончательный ответ  найден;
найден;
- Условие не выполнено и 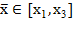 , то следует выбрать наилучшую точку (
, то следует выбрать наилучшую точку (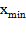 или
или  ) и две точки по обе стороны от нее;
) и две точки по обе стороны от нее;
- Условие не выполнено и 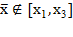 , то следует принять, что
, то следует принять, что 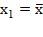 и перейти на шаг 2.
и перейти на шаг 2.
Опишем один из возможных вариантов реализации метода Пауэлла на языке php с применением html.
Данная реализация будет состоять из двух php-страниц, на первой из которой будут вводиться непосредственно первоначальные данные задачи (функция, начальная точка, шаг и точность). Если начальные данные будут введены верно и без ошибок, то после нажатия на кнопку будет выведен результат решения задачи на второй странице.
На первой странице для ввода первоначальных данных будет находиться 4 текстовых поля для ввода и кнопка, выполняющая функцию подсчета.
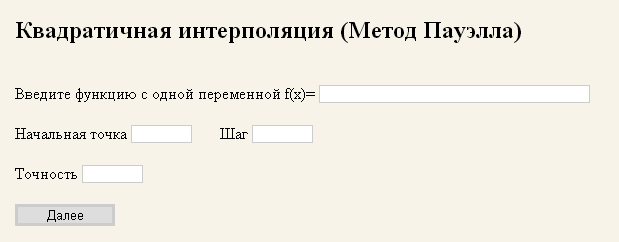
Рис. 1. Вариант расположения элементов на странице для ввода начальных данных
Код страницы для ввода первоначальных данных выглядит следующим образом:
<html>
<head>
<title>Метод Пауэлла</title>
<meta http-equiv='Content-type' content='text/html; charset=windows-1251'>
<link rel=stylesheet href='main.css' type='text/css'>
</head>
<body>
<h2>Квадратичная интерполяция (Метод Пауэлла)</h2><br>
<form action="kvadr_interpol_rez.php" method="post">
Введите функцию с одной переменной f(x)=
<input type="text" size="40" name="function1"><br>
Начальная точка<input type="text" size="5" name="x1">
Шаг<input type="text" size="5" name="step"><br>
Точность<input type="text" size="5" name="toch"><br>
<input type="submit" value="Далее">
</form>
</body>
</html>
После нажатия на кнопку «Далее» происходит загрузка второй страницы kvadr_interpol_rez.php и с помощью метода post передаются значения переменных function1 (функция), x1 (начальная точка), step (шаг) и toch (точность). Стоит заметить, что в функции, введенной пользователем, в качестве переменной обязательно выступает буква х и она может иметь в своем составе экспоненту и натуральный логарифм.
Далее подробно и по частям рассмотрим код второй основной страницы, в которой реализован сам метод.
Для начала необходимо написать функцию в php, которая будет считывать функции, введенные пользователем для оптимизации. Она может выглядеть следующим образом:
function func1($arg)
{
$str=$_POST['function1']; //получили функцию пользователя в виде строки
//если встречается в функции exp(), т.е. эспонента
if (strpos($str, "exp")!==false)
{
$s1 = strpos($str, "exp"); //позиция с которой начинается exp
$s2 = strpos($str, ")", $s1); //номер элемента, где кончается exp
$expon=substr($str, $s1, $s2+1); //вырезаем выражение экспоненты
$s1 = strpos($expon, "("); //позиция “(“
$s2 = strpos($expon, ")"); //позиция “)“
$s1 = substr($expon, $s1, $s2); //вырезает выражение под экспонентой
$s1 = str_replace("x",$arg,$s1);//заменяем все x на аргумент в функции
//подсчитаем выражение под знаком exp
$vexp = (float) preg_replace( '/([0-9\(\)\*\-\+\/\.]*)/e', '\\1', $s1 );
$rezexp=exp($vexp);//вычисляем непосредственно экспоненту
//замена выражения exp() в строке $str на посчитанное число
$str = str_replace($expon,$rezexp,$str);
}
//если встречается в функции пользователя ln(), т.е. натуральный логарифм
if (strpos($str, "ln")!==false)
{
$l1 = strpos($str, "ln"); // позиция, с которой начинается ln()
$l2 = strpos($str, ")", $l1); // конец выражения ln()
$lnln=substr($str, $l1, $l2+1); // все выражение логарифма
$l1 = strpos($lnln, "(" );
$l2 = strpos($lnln, ")" );
$l1 = substr($lnln, $l1, $l2); //вырезает выражение под логарифмом
$l1 = str_replace("x",$arg,$l1); //заменяем все x на переданный аргумент
//подсчитаем выражение под знаком логарифма
$vln = (float) preg_replace( '/([0-9\(\)\*\-\+\/\.]*)/e', '\\1', $l1 );
$rezln=log($vln); //вычисляем непосредственно натуральный логарифм
$str = str_replace($lnln,$rezln,$str);//замена ln() на посчитанное число
}
//замена х на переданное число
$str = str_replace("x",$arg,$str);
//результат
$str = (float) preg_replace( '/([0-9\(\)\*\-\+\/\.]*)/e', '\\1', $str );
return $str;
}
Функция func1() преобразует функцию пользователя, которая введена в виде строки, в настоящую функцию, в которую можно подставлять любые значения и получать результат.
Для удобства вставим в код php-функцию подсчета полинома по формуле (8):
function polinom($x,$y,$z,$fx,$fy,$fz)
{
$rez=0.5*((($y*$y-$z*$z)*$fx+($z*$z-$x*$x)*$fy+($x*$x-$y*$y)*$fz)/(($y-$z)*$fx+($z-$x)*$fy+($x-$y)*$fz));
return $rez;
}
Теперь начнем описание основной части алгоритма. Рассмотрим первый кусок кода:
// получаем значения начальных данных
$function1=$_POST['function1'];
$x1 = $_POST['x1'];
$step = $_POST['step'];
$toch = $_POST['toch'];
echo "Функция f(x) = ",$function1,"<br>";
echo "начальная точка x1 = ",$x1,"<br>","шаг ",$step,"<br>";
echo "1 итерация","<br>";
$x2=$x1+$step; // вычисляем х2
$f1 = func1($x1); // вычисляем f(x1)
$f2 = func1($x2); // вычисляем f(x2)
if ($f1 > $f2) { $x3=$x1+2*$step;} else {$x3=$x1-$step;} // вычисляем х3
$f3 = func1($x3);
$fmin=min($f1,min($f2,$f3)); // находим минимальное среди f(x1), f(x2), f(x3)
//поиск xmin
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) {$xmin=$x2;}
if ($fmin == $f3) {$xmin=$x3;}
//вычислим знаменатель полинома и проверим его на 0
$znam=($x2-$x3)*$f1+($x3-$x1)*$f2+($x1-$x2)*$f3;
while ($znam == 0) {
//если знаменатель 0, то х1=Xmin и заново пересчитываем
$x1 = $xmin; $x2=$x1+$step; $f1 = func1($x1); $f2 = func1($x2);
if ($f1 > $f2) {$x3=$x1+2*$step;} else {$x3=$x1-$step;}
$f3 = func1($x3);
$fmin=min($f1,min($f2,$f3));
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) {$xmin=$x2;}
if ($fmin == $f3) {$xmin=$x3;}
}
$sr=polinom($x1,$x2,$x3,$f1,$f2,$f3); //вычислим значение по формуле (8)
$fsr=func1($sr);
echo "x = ",$sr,"<br>";
echo "f(x) = ",$fsr,"<br>";
$l=0; //счетчик циклов
Данная часть кода содержит в себе первую итерацию алгоритма, в которой вычисляются первые значения 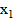 ,
, 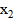 ,
, 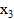 ,
,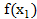 ,
, 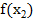 и
и 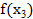 , находятся минимальные значения
, находятся минимальные значения 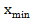 и
и 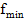 , а также значение аппроксимации точки минимума по формуле (8).
, а также значение аппроксимации точки минимума по формуле (8).
Рассмотрим второй кусок кода, который проверяет условия на точность вычисления и выводит окончательный ответ:
while ((($fmin-$fsr) > $toch) || (($fmin-$fsr) < -$toch))
// пока не достигнута заданная точность
{
$l=$l+1; // счетчик итераций
echo $l+1," итерация","<br>";
// ПЕРВЫЙ СЛУЧАЙ, если 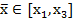 (где
(где 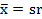 )
)
if (($sr >= min($x1,min($x2,$x3))) && ($sr <= max($x1,max($x2,$x3))))
{
// выбор наилучшей точки и двух точек по бокам
if ($xmin < $sr) // если лучшей точкой является Xmin
{ // создаем массив всех точек
if ($xmin == $x1) { $massiv[0]=$xmin; $massiv[1]=$x2; $massiv[2]=$x3; $massiv[3]=$sr;}
if ($xmin == $x2) { $massiv[0]=$xmin; $massiv[1]=$x1; $massiv[2]=$x3; $massiv[3]=$sr;}
if ($xmin == $x3) { $massiv[0]=$xmin; $massiv[1]=$x1; $massiv[2]=$x2; $massiv[3]=$sr;}
// сортируем массив методом пузырька по возрастанию
for ($j = 0; $j < count($massiv)-2; $j++) {
for ($i = 0; $i < count($massiv)-$j-1; $i++) {
if ($massiv[$i]>$massiv[$i+1])
{$m=$massiv[$i+1];$massiv[$i+1]=$massiv[$i];$massiv[$i]=$m; }}}
//располагаем точки в правильном порядке
if (($massiv[0] == $xmin) || ($massiv[1] == $xmin)) {$x1=$massiv[0];$x2=$massiv[1];$x3=$massiv[2];}
if (($massiv[2] == $xmin) || ($massiv[3] == $xmin)) {$x1=$massiv[1];$x2=$massiv[2];$x3=$massiv[3];}
$f1=func1($x1);
$f2=func1($x2);
$f3=func1($x3);
$fmin=min($f1,min($f2,$f3));
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) {$xmin=$x2;}
if ($fmin == $f3) {$xmin=$x3;}
//вычислим знаменатель и проверим его на 0
$znam=($x2-$x3)*$f1+($x3-$x1)*$f2+($x1-$x2)*$f3;
while ($znam == 0) {
$x1 = $xmin; $x2=$x1+$step; $f1 = func1($x1); $f2 = func1($x2);
if ($f1 > $f2) {$x3=$x1+2*$step;} else {$x3=$x1-$step;}
$f3 = func1($x3);
$fmin=min($f1,min($f2,$f3));
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) { $xmin=$x2;}
if ($fmin == $f3) {$xmin=$x3;}}
//вычисляем ответ
$sr=polinom($x1,$x2,$x3,$f1,$f2,$f3);
$fsr=func1($sr);
echo "x = ",$sr,"<br>";
echo "f(x) = ",$fsr,"<br>";
}
else //в противном случае, т.е. если лучшей точкой является sr
{
// заполняем массив
$massiv[0]=$sr; $massiv[1]=$x1; $massiv[2]=$x2; $massiv[3]=$x3;
//сортируем массив точек
for ($j = 0; $j < count($massiv)-2; $j++) {
for ($i = 0; $i < count($massiv)-1-$j; $i++) {
if ($massiv[$i]>$massiv[$i+1])
{$m=$massiv[$i+1]; $massiv[$i+1]=$massiv[$i];$massiv[$i]=$m; }}}
if (($massiv[0] == $sr) || ($massiv[1] == $sr)) {$x1=$massiv[0];$x2=$massiv[1];$x3=$massiv[2];}
if (($massiv[2] == $sr) || ($massiv[3] == $sr)) {$x1=$massiv[1];$x2=$massiv[2];$x3=$massiv[3];}
$f1=func1($x1); $f2=func1($x2); $f3=func1($x3);
$fmin=min($f1,min($f2,$f3));
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) {$xmin=$x2;}
if ($fmin == $f3) {$xmin=$x3;}
//проверим знаменатель
$znam=($x2-$x3)*$f1+($x3-$x1)*$f2+($x1-$x2)*$f3;
while ($znam == 0) {
$x1 = $xmin; $x2=$x1+$step; $f1 = func1($x1); $f2 = func1($x2);
if ($f1 > $f2) {$x3=$x1+2*$step;} else {$x3=$x1-$step;}
$f3 = func1($x3);
$fmin=min($f1,min($f2,$f3));
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) {$xmin=$x2;}
if ($fmin == $f3) { $xmin=$x3;}}
//вычислим ответ данной итерации
$sr=polinom($x1,$x2,$x3,$f1,$f2,$f3);
$fsr=func1($sr);
echo "x = ",$sr,"<br>";
echo "f(x) = ",$fsr,"<br>";
}
}
//ВТОРОЙ СЛУЧАЙ, если 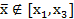 (где
(где 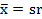 )
)
else
{
// вычисление х1, х2, f1, f2, x3, f3, fmin
$x1=$sr; $x2=$x1+$step;
$f1=func1($x1); $f2=func1($x2);
if ($f1 > $f2) {$x3=$x1+2*$step;} else { $x3=$x1-$step;}
$f3 = func1($x3);
$fmin=min($f1,min($f2,$f3));
//поиск xmin
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) {$xmin=$x2;}
if ($fmin == $f3) {$xmin=$x3;}
//вычислим знаменатель и проверим его на 0
$znam=($x2-$x3)*$f1+($x3-$x1)*$f2+($x1-$x2)*$f3;
while ($znam == 0) {
$x1 = $xmin; $x2=$x1+$step; $f1 = func1($x1); $f2 = func1($x2);
if ($f1 > $f2) { $x3=$x1+2*$step;} else { $x3=$x1-$step;}
$f3 = func1($x3);
$fmin=min($f1,min($f2,$f3));
if ($fmin == $f1) {$xmin=$x1;}
if ($fmin == $f2) {$xmin=$x2;}
if ($fmin == $f3) {$xmin=$x3;}
}
$sr=polinom($x1,$x2,$x3,$f1,$f2,$f3);
$fsr=func1($sr);
echo "x = ",$sr,"<br>";
echo "f(x) = ",$fsr,"<br>";
}
}
echo "Ответ: x = ",$sr;
Метод хоть и оказался громоздким, но очень понятен и прост. Пока не будут выполнены условия на точность, просчитываются новые значения переменной sr (или 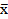 ) по формуле (8). В первом случае, когда sr принадлежит промежуткам между
) по формуле (8). В первом случае, когда sr принадлежит промежуткам между 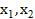 и
и 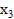 , выбирается лучшая (т. е. наименьшая) точка из точек
, выбирается лучшая (т. е. наименьшая) точка из точек 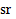 и xmin. Создается упорядоченный массив из всех найденных точек (
и xmin. Создается упорядоченный массив из всех найденных точек (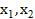 ,
, 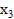 ,
, 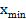 ,
, 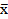 ), кроме точки, которая равна
), кроме точки, которая равна 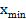 . Далее выбираем три основных точки (
. Далее выбираем три основных точки (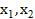 ,
, 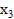 ) из найденного массива, по принципу, что лучшая точка должна находится посередине или же с краю, если это невозможно. После выбора трех основных точек повторяются вычисления с 4 шага алгоритма. Во втором же случае, когда sr не принадлежит промежуткам между
) из найденного массива, по принципу, что лучшая точка должна находится посередине или же с краю, если это невозможно. После выбора трех основных точек повторяются вычисления с 4 шага алгоритма. Во втором же случае, когда sr не принадлежит промежуткам между 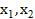 и
и 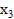 , просто предполагаем, что
, просто предполагаем, что 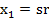 и переходим на шаг 2 алгоритма метода Пауэлла.
и переходим на шаг 2 алгоритма метода Пауэлла.
Для наглядности и уверенности в работе приведенного алгоритма ниже покажем скриншоты второй страницы.

Рис. 2. Первый пример результата работы программы

Рис. 2. Второй пример результата работы программы

Рис. 2. Третий пример результата работы программы
Литература:
1. Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. — М.: Радио и связь, 1988–128 с.
2. Методы оптимизации систем автоматизированного проектирования. Метод Пауэлла. http://optimizaciya-sapr.narod.ru/bez_odnomer/paul.html







