Об использовании коллинеарной точки либрации при решении задачи кометно-астероидной опасности

В статье рассматриваются вопросы, связанные с проблемой кометно-астероидной опасности. Предлагается метод для мониторинга околоземного космического пространства посредством КА, который функционирует в окрестности коллинеарной точки либрации (L₁, L₂) системы Солнце—Земля и в околоземном космическом пространстве. Приводятся численные примеры.

Ключевые слова:кометно-астероидная опасность, мониторинг, околоземное космическое пространство, точка либрации.

Введение. В настоящий момент одним из наиболее известных событий, которое может произойти и причинить катастрофические последствия для Земли, является ее столкновение с кометой или астероидом.

В рамках программы обнаружения потенциально опасных космических объектов по данным Национального управления США по аэронавтике и исследованию космического пространства (NASA) существует более тысячи потенциально опасных астероидов, траектории которых пересекают окрестность орбиты Земли. За последнее время в связи с совершенствованием наблюдательных технологий количество таких объектов существенно возросло.

По мнению ученых, вероятность такого события мала по сравнению с автомобильной катастрофой или пожаром, но последствия могут носить глобальный характер. Считается, что их причиной могут быть астероиды размером 1–2 км в диаметре. Для того, чтобы уменьшить риск столкновения проводятся программы обнаружения потенциально опасных объектов (ПОО), которые могут в будущем столкнуться с Землей, в тоже время совершенствуются технологии и разрабатываются проекты по предотвращению угрозы столкновения. Опасность, которой обладает астероид или комета по отношению к Земле определяется двумя параметрами: вероятностью столкновения с Землей и собственной кинетической энергией.

Оценка последствий столкновения с ПОО не только зависит от размера небесного тела, его массы и скорости столкновения с Землей, а также от его формы и вращательного движения вокруг своей оси. С 1998 года NASA реализует программу Spaceguart Survey по обнаружению астероидов сближающихся с Землей (АСЗ), к настоящему моменту уже обнаружено 95 % АСЗ с размером в диаметре более 1 км.

Для объективной оценки степени опасности для земной биосферы американским астрономом Ричардом Бинзелом (R. Binzel) была разработана качественная шкала оценки опасности столкновения с Землей, которая впервые была представлена на симпозиуме в Турине и получила свое название в честь этого города (The Torino Impact Hazard Scale), а в конце июля 1999 г. шкала была утверждена международным астрономическим сообществом (рис. 1). Балл по Туринской шкале астероидной опасности присваивается малому телу Солнечной системы в момент его открытия в зависимости от массы этого тела, возможной скорости и вероятности его столкновения с Землей. Она позволяет классифицировать астероиды и другие небесные тела (с учетом их размера и скорости относительно нашей планеты) по 11 уровням степени их опасности.

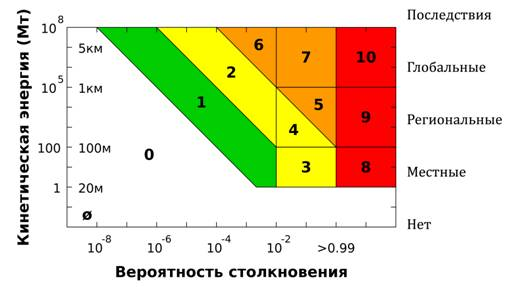
Рис. 1. Туринская шкала астероидной опасности

Туринская шкала астероидной опасности учитывает не только вероятность столкновения астероида с Землей, но и потенциальные разрушения, к которым может привести катастрофа столкновения: местные — причиняется ущерб на относительно небольшой территории, при котором возможна гибель людей; региональные — разрушения могут охватывать миллионы квадратных километров, они эквивалентны крупнейшим землетрясениям, извержениям вулканов, взрывам ядерной бомбы. Очень большая вероятность гибели людей; глобальные — разрушения, которые имеют планетарный масштаб.

Таким образом, астероидно-кометная опасность не только социальная проблема, целью которой является общественная безопасность, но и научная, когда необходимо совершенствование/создание средств (наземные и космические телескопы) и методов (космические проекты и программы) по предотвращению угрозы столкновения.

Методы предотвращения угрозы. Европейское космическое агентство (ESA) разрабатывает проект под названием «Дон Кихот» (Don Quijote) отражения астероидной атаки путем прямого столкновения космического аппарата (КА) с опасным астероидом с целью изменения его траектории.

Существует и менее активный способ смещения астероида с опасной траектории, который получил название «Гравитационный трактор» (Gravity tractor). В данном случае для достижения поставленной цели необходимо, чтобы КА достаточно большой массы продолжительное время двигался в непосредственной близости от астероида и, воздействуя на него силой всемирного тяготения, изменял его траекторию.

Например, для изменения скорости астероида на 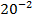 м/с, масса которого  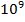кг, необходимо действовать на промежутке времени порядка  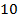лет постоянной силой приблизительно равной  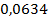Н. Такая сила может быть обеспечена КА, масса которого около  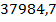кг, на расстоянии  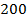м от центра инерции астероида.

Экзотический способ, предполагающий создание вблизи астероида облака небольших зеркал, был представлен профессором университета Глазго (University of Glasgow) Миссимилиано Вазиле (Massimiliano Vasile). Отражая солнечный свет на поверхность астероида, они способны нагреть его до температуры, необходимой для испарения его вещества, и за счет реактивного эффекта от испаряющихся газов астероид будет медленно смещаться со своей траектории.

Также рассматриваются варианты предполагающие: уничтожения астероида ядерным взрывом; изменение его траектории путем сообщения астероиду дополнительной скорости системой ядерных взрывов на его поверхности, двигателями реактивной тяги КА, рассеяния пылевого облака на пути движения астероида, направленного сброса вещества с его поверхности; окраска части поверхности астероида с целью изменения его отражательной способности и получения дополнительного импульса.

Следует отметить, что несмотря на все разрабатываемые проекты проблема защиты Земли от столкновения с астероидом или кометой до сих пор остается открытой, поэтому можно сказать, что основной проблемой является проблема своевременного обнаружения потенциально опасных объектов.

Использование коллинеарной точки либрации. В качестве первоочередных задач для решения проблемы астероидно-кометной опасности может являться задача мониторинга околоземного космического пространства или задача перехвата космического объекта.

Эти задачи могут быть решены КА, расположенным в окрестности коллинеарной точки либрации L₁ или L₂ [1], который может быть многократно использован для исследования космических объектов, пролетающих около Земли. В результате, зная информацию о строении, физическом составе, рельефе поверхности, можно будет оптимизировать действия по предотвращению угрозы, используя наиболее эффективные технические средства с целью изменения траектории, либо расщепления астероида или кометы на достаточно мелкие фрагменты.

Уравнения движения КА во вращающейся системе координат могут быть представлены в виде [2]

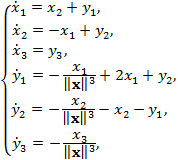                                                                                          (1)

здесь 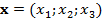 — вектор координат КА,  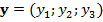— вектор импульсов, центр инерции Земли совпадает с началом системы координат, а ось  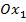направлена вдоль оси, соединяющей центры масс Земли и Солнца,  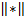— евклидова норма вектора. В принятой модели единицы времени и расстояния выбраны таким образом, что единица расстояния приблизительно равна  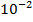а. е., а единица времени — год, деленный на 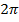. Точки либрации L₁, L₂ во вращающейся системе неподвижны и имеют координаты , 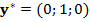и 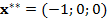, , 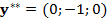соответственно.

Система (1) — гамильтонова, где функция Гамильтона

                                                          (2)

Известно, что гамильтониан (2) на траекториях движения сохраняет свое значение, т. е. является интегралом для системы (1). Этот факт может быть использован для оценки точности приводимых примеров численного интегрирования.

Примеры траекторий движения. Рассмотрим численные примеры мониторинга околоземного космического пространства. Смоделируем применение управляющего воздействия в виде малого изменения скорости КА, находящегося в окрестности коллинеарной точки либрации L₁. Результаты численного моделирования движения КА в плоскости эклиптики (пусть в начальный момент 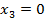,) приведены на рис. 2 и рис. 3.

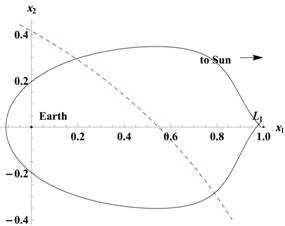
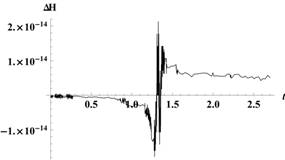
Рис. 2. Траектория с возвращением в окрестность точки либрации L₁ на промежутке времени около 5 месяцев и соответствующий ей график приращения гамильтониана

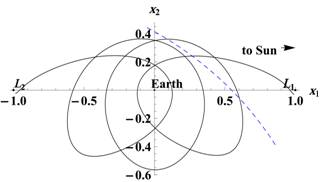
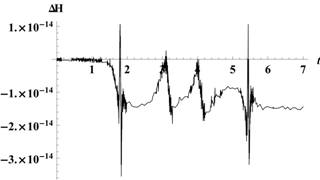
Рис. 3. Траектория с возвращением в окрестность точки либрации L₂ на промежутке времени около 13,5 месяца и соответствующий ей график приращения гамильтониана

На рис. 2 видно, что с помощью весьма малого воздействия КА совершает протяженный маневр в околоземном космическом пространстве, время движения по траекториям — порядка нескольких месяцев. На рис. 3 КА совершает маневр с возвращением в окрестность точки либрации L₂, которому соответствует больший промежуток времени. Начальный момент времени и способ применения управляющего воздействия подбираются так, чтобы обеспечить сближение с изучаемым небесным телом, траектория которого на рисунках обозначена пунктиром.

Заключение. Таким образом, можно сказать, что окрестность фазового пространства коллинеарной точки либрации обладает свойством, позволяющим совершать маневры, обеспечивающие наблюдение за околоземным космическим пространством. Здесь можно использовать малое управляющее воздействие, которое становится эффективным в силу неустойчивости коллинеарной точки либрации. Именно в этом случае неустойчивость является положительным фактором, позволяющим при малых энергетических затратах существенно изменить траекторию движения [3].

Очевидно, что такого типа КА может быть многократно использован для исследования околоземного космического пространства. Следует отметить, что при совершении такого маневра возникают задачи построения «траектории возвращения» [3, 4], когда КА в конечной точке траектории попадает в окрестность устойчивого многообразия вблизи коллинеарной точки либрации, и дальнейшей его стабилизации [2–8].

Литература:

1.         Маркеев А. П. Точки либрации в небесной механике и космодинамике. М.: Наука, 1978. 312 с.

2.         Шмыров В. А. Стабилизация управляемого орбитального движения космического аппарата в окрестности коллинеарной точки либрации L₁ // Вестн. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. 2005. Вып. 2. С. 193–199.

3.         Шиманчук Д. В., Шмыров А. С., Построение траектории возвращения в окрестность коллинеарной точки либрации системы Солнце—Земля // Вестн. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. 2013. Вып. 2. С. 76–85.

4.         Kulakov F., Shmyrov A., Shymanchuk D. Supervisory Remote Control of Space Robot in an Unstable Libration Point // Proceedings — 7th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing System: Technology and Applications 12–14 September 2013, Berlin, Germany. Berlin, 2013. Vol. 2. P. 925–928

5.         Shmyrov A., Shmyrov V. Controllable orbital motion in a neighborhood of collinear libration point // Applied Mathematical Sciences, 2014. Vol. 8, № 10. P. 487–492.

6.         Шмыров А. С., Шмыров В. А. Синтез оптимального управления орбитальным движением в окрестности коллинеарной точки либрации // Вестн. С.-Петерб. ун-та. Сер. 1: Математика, механика, астрономия, 2012. Вып. 4. С. 139–146.

7.         Шиманчук Д. В. Моделирование орбитального управляемого движения космического аппарата в окрестности коллинеарной точки либрации L₁ // Вестн. С.-Петерб. ун-та. Сер. 10: Прикладная математика, информатика, процессы управления. 2010. Вып. 3. С. 86–92.

8.         Шиманчук Д. В., Шмыров В. А. Проблемы стабилизации орбитального движения космического аппарата в окрестности коллинеарной точки либрации // Молодой ученый. — 2014. — № 3. — С. 20–24.