О явной форме сил реакций сервосвязей

В работе получены уравнения движения механических систем, стесненных геометрическими и кинематическими сервосвязями, а также рассматриваются вопросы их устойчивости.

Пусть механическая система, положение которой определяется обобщенными координатами q₁, …,q_n, стеснена неголомными идеальными связями:    

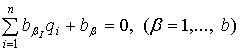                                                                           (1)

а также сервосвязями вида

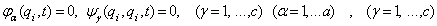                          (2)

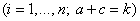
Предполагается, что среди возможных перемещений, допускаемых связями (1) имеются такие, определяемые уравнениями:

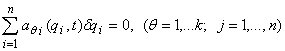                                                                (3)

на которых реакции сил реакций связей второго рода работы не производят /1/. Имея в виду параметрическое освобождение системы от сервосвязей /2, 3/ введем дополнительные независимые параметры h_р, 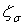, соответствующие преобразованию системы с сервосвязями (2) к виду:

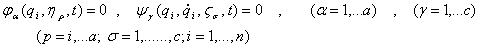               (4)

где h_p, 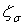 — параметры, характеризирующие освобождение системы от первой и второй групп сервосвязей (2)

Обозначив через N_p и P_s принуждения реакций, отнесенные к параметрам h_р, 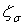, будем предполагать, что последние вынужденно изменяются согласно дифферинциальным уравнениям /3/.

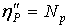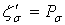,  (р=1,…,а, 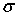=1,…,с)                                                            (5)

С учетом первых групп уравнений (2), (4) вместо обобщенных координат 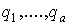 введем параметры 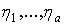. Соотношениями, тождественно удовлетворяющими уравнениям (1) и второй группе (4) введем скоростные параметры e_v /5/:

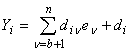                                                                                                      (6)

где

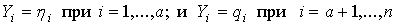
и за а+с=к скоростных параметров e_v выберем h_р, 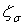. Тогда уравнения (3) в неголономных координатах будут иметь вид

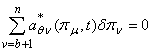                                                                                                 (7)

где p_n — квазикоордината, соответствующая квазискорости e_n/5/. Из преобразованного общего уравнения динамики /5/

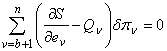
на (А) — перемещениях (7) получим уравнения движения с множителями сервосвязей:

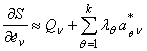                                                                                                  (8)

где S — энергия ускорений системы; l_q — множители сервосвязей.

Предположим, что все связи, налагаемые на систему, стационарны. Тогда энергия ускорений параметрически освобожденной системы будет иметь вид

,

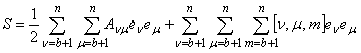где [n, m, m]- символы Кристоффеля первого рода /5/.

Записывая последнее выражение в развернутом виде через а квазискоростей h_a, с квазискоростей 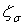 и n-k-bквазискоростей е_k+rиформируя реакция связей второго рода по законам:

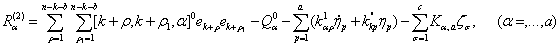
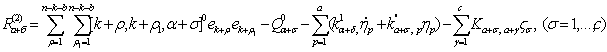
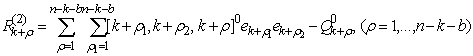
где 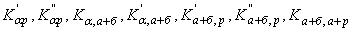 — положительные постоянные; нолик наверху соответствует невозмущенному движению. Подставляем их в уравнения (8). Далее из п-к-в уравнений полученной системы определяя  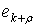и подставляя их в (а+с) уравнений полученной системы, получим уравнения возмущенного движения:

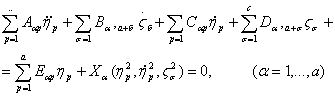
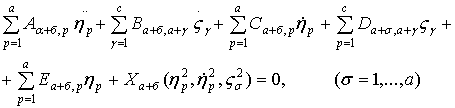                     (9)

где A_ap, B_a,а+б, С_aр, D_a,а+б, Е_aр, А_а+б,р, В_а+б,а+р, С_а+б,_р, D_{а+б, а+р}, Е_{а+б, р} -некоторые функции h_р, z_б, е_к+р. Устойчивость невозмущенного движения h_р=0, 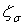=0 будем исследовать используя методы исследований устойчивости неустановившихся систем /7/. Эти условия имеют вид

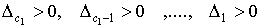                                                                      (10)

где 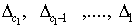 — главные диагональные миноры 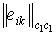квадратичной формы

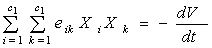
Так как e_ik (i,k=1,…,c₁) являются переменными, то для определенной отрицательности (dv/dt), вообще говоря, недостаточно выполнения условий (9). Неравенства Сильвестра должны выполнятся равномерно по всем X_i, t, т. е. следует потребовать выполнения неравенств:

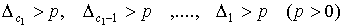                                                 (11)

Условия (10) и (11) выражают условия асимптотической устойчивости системы (9).

Пример. Рассмотрим задачу о качении без скольжения однородного шара радиуса R по материальной плоскости Р. Сохраняя обозначения ([1], п. 21), будем предполагать, что плоскость Р, на которую действуют силы реакции сервосвязей, имеет массу m₁.

На систему, движение которой стеснено связями первого рода

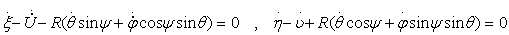        (12)

должны быть наложены сервосвязи

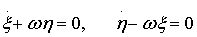                                                                                      (13)

Наряду с (13) в системе удовлетворяются соотношения

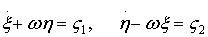                                                                                   (14)

где z₁×z₂ — параметры, характеризующие освобождение системы от сервосвязей (13). Соотношениями

,

,

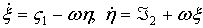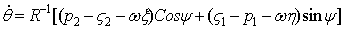
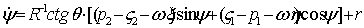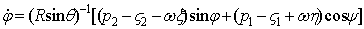
тождественно удовлетворяющими условиями (12) и (14), введем скоростные параметры 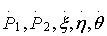. Преобразуя энергию ускорений к этим переменным и составляя уравнения движения в форме (8), получим

,

,

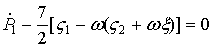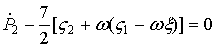
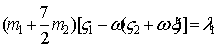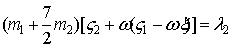                                                                             (15)

где l_1,l₂ — силы реакций сервосвязей.

К системе (15) присоединяем уравнения

z₁= — К₁z₁-К₂z₂, z₂= — К₃z₁-К₄z₂

где К₁, К₂, К₃, К_4 — некоторые постоянные.

Если реакции сервосвязей l₁ и l₂ формировать по законам:

l₁=m₂p_1 — mw²x — k ₁z₁– k₂z₂,l₂=m₂p_2 — mw²h — k ₃z₁– k₄z₂

то, поставляя их в (15) относительно z₁, z₂, получим систему

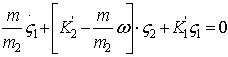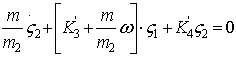,                  (16)

где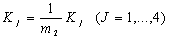

Так как система (16) представляет собой систему дифференциальных уравнений с постоянными коэффициентами, то условия устойчивости ее нулевого решения z₁=0, z₂=0 могут быть найдены теоремой Гурвица [6].

Эти условия имеют вид:

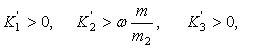К^́₄>0                                                            (17)

Условия (17) показывают, что необходимые и достаточные условия устойчивого осуществления сервосвязей (13) зависят лишь от выбора постоянных K^́₁, K^́₂, K^́₃ и К^́₄..

Литература:

1.   Беген А. Теория гигроскопических компасов. М.Наука, 1967.

2.   Азизов А. Г. Об уравнениях динамики систем с сервосвязями. Научные труды. ТашГУ. 1975. вып. 476.

3.   Азизов А. Г. Прикладные задачи динамики управляемых систем. Учебное пособие, Ташкент, 1980.

4.   Румянцев В. В. О движении некоторых систем с неидеальными связями. Вестник МГУ. Сер. Матем. Механ. 1961.

5.   Лурье А. И. Аналитическая механика. М. Физматгиз. 1961.

6.   Маркен Г. Д. Введение в теорию устойчивости. — М.: Наука, 1987.

7.   Красовский Н. Н. Некоторые задачи теории устойчивости движения. — М.: Физматгиз, 1959.