В статье приведено описание структурных линий рельефа и их математическая интерпретация для последующего цифрового и геометрического моделирования.
Ключевые слова: горизонтали, линии наибольшего ската, водоразделы, тальвеги, линии изохрон.
Большинство инженерных задач, связанных с проектированием поверхности для строительства инженерных сооружений, градостроительства, ландшафтной архитектуры, сельскохозяйственной мелиорации связано с анализом и преобразованием геометрических данных топографической поверхности (ТП). Построение сети специальных линий на ТП необходимо в практике проектирования. На современном уровне имеются следующие типы структурных линий ТП:
- профильные сечения;
- горизонтали поверхности (изолинии);
- линии наибольшего ската;
- линия водораздела (линия хребта);
- линия тальвега (водослив);
Современные ГИС-программы имеют возможность автоматизации построения профильных сечений и горизонтальных линий поверхности по предварительно заданным параметрам, но не имеется возможности автоматизированного построения линий наибольшего ската, водораздела, тальвега. Очевидно, проблема состоит в нерешенности определений данных терминологий, что создает проблемы при их программировании. Построение профильных сечений и изолиний в ГИС-программах рассматривается как пересечение плоскости с некоторым множеством — интерполяционной поверхностью, заданной матрицей X,Y,Z данных.
Если рассматривать ТП как некоторое множество, то следует установить определения структурных линий на базе подмножеств, классов.
Для ТП выделение одного класса подмножества основывается на условии выделения базового класса. Следует определить тот базовый класс подмножества, который впоследствии будет основой для выделения других классов.
Подмножество 1-го класса. Множество ТП имеет подмножество совокупности всех точек одного уровня h(значения Z), которое определяет горизонтальную плоскость, пересекающую множества и образующую плоскую кривую.
Данная плоская кривая называется горизонтальной линией и ГИС-программы, очевидно, основываются на данном определении при построении изолиний.
Несколько элементов подмножества данного класса составляют некоторое семейство. Условием создания семейства является:
hn — hn-1= h (const.),
что устанавливает параметр — уровень проведения изолиний.
Подмножество 2-го класса. Интерполяция точек, расположенных в семействе подмножества 1-го класса с наименьшим интервалом между уровнями hn, hn-1, …, h0 является линией, называемой «линия наибольшего ската» [1–4], «линия падения» [4].
Условие «с наименьшим интервалом» устанавливает направление нормали между двумя уровнями. Условие hn, hn-1, …, h0устанавливает последовательность направления нормали в убывающем порядке.
Подмножество 3-го класса. Интерполяция точек, расположенных в семействе подмножества 1-го класса в положительных дугах максимальной кривизны между уровнями hn, hn-1, …, h0является линией, называемой «водораздел», «линия хребта» [4].
Условие «в положительных дугах» выделяет дуги, центры которых принадлежат множеству ТП.
hn, hn-1, …, h0 — условие последовательности действий.
Подмножество 4-го класса. Интерполяция точек, расположенных в семействе подмножества 1-го класса в отрицательных дугах максимальной кривизны между уровнями hn, hn-1, …, h0 является линией, называемой «водослив», «тальвег» [4] (Рис. 1).
Условие «в отрицательных дугах» выделяет дуги, центры которых не принадлежат множеству ТП, они расположены за пределами поверхности.
hn, hn-1, …, h0 — также условие последовательности действий.
Водораздел и тальвег являются частными случаями линии наибольшего ската. Выделение подмножеств 3-го и 4-го класса из множества ТП выделяет так называемые особые линии поверхности.
Особенность 1. Водяные струи, распределяясь по поверхности, всегда стремятся от линии водораздела к линии водослива [4].
Особенность 2. В узлах линии водораздела могут иметься три и более нормали, направленных к нижнему уровню (рис. 1, точка W).
Особенность 3. В окрестностях тальвега имеются линии наибольшего ската, примыкающие к нему и образующие пучок линий (Рис. 1 точка S).
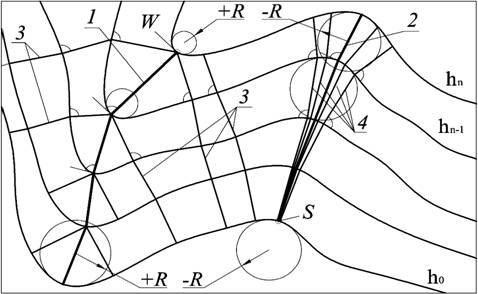
Рис. 1. Особые линии поверхности: 1 — Водораздел; 2 — Тальвег; 3,4 — линии наибольшего ската. W — перекресток линий наибольшего ската; S — пучок линий наибольшего ската.
Так как линии наибольшего ската, по сути, являются траекториями движения некоторой материальной точки по поверхности, то выделение подмножеств по вышеуказанным определениям способствуют выделению другого, пятого класса.
Подмножество 5-го класса. Интерполяция точек семейства подмножества 2-го класса (линии наибольшего ската) в заданном промежутке времени является линией, называемой «линия изохрон», «линия равного добегания».
Этот класс подмножества выделяет узлы интерполяции на линиях наибольшего ската, при этом условием выделения является пройденный путь материальной точки за определенный промежуток времени. Следует отметить, что нужно выбрать стартовую линию для начала отсчета, каковым является изолиния высшего порядка. Если рассматривать материальную точку как некоторую массу воды, то очевидно линия изохрон определит линию равного добегания воды по поверхности, что наиболее важно при решении инженерных задач, связанных с проектированием водоотводной сети с поверхности, определением участков, наиболее подвергаемых водной эрозии и т. д. (Рис. 2)
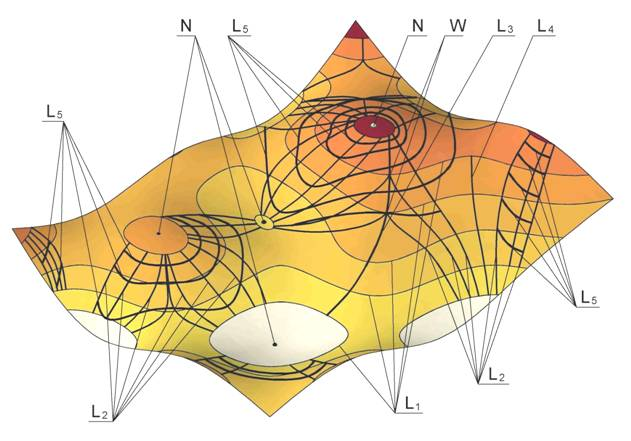
Рис. 2 — Построение сети специальных линий ТП. N — критическая точка; W — перекресток; L1 — горизонтали; L2 — линии наибольшего ската; L3 — водораздел; L4 — тальвег; L5 — линии изохрон;
ЦМР, построенная по вышеуказанным специальным линиям ТП, является наиболее информативной для решения ряда инженерных задач, связанных с проектированием проектной поверхности.
Литература:
1. Крылов Н. Н. и др. Начертательная геометрия. — М.: Высшая школа, 1990. — С. 79–103.
2. Фролов С. А. Начертательная геометрия. — М.: Машиностроение, 1978. — С. 30–92.
3. Климухин А. Г. Начертательная геометрия. — М.: Стройиздат, 1973. — С. 50–68, 89–92.
4. Брилинг Н. С. Строительное и топографическое черчение. — М.: Просвещение, 1980. — С. 140–167.







