С развитием различных способов инвестирования и растущей информированностью населения о фондовом рынке, инвестиционные компании предлагают клиентам различные интегрированные продукты, тем самым удовлетворяя запросы даже самых требовательных клиентов. В связи с этим актуально рассмотреть построение интегрированного продукта на примере рынка ценных бумаг Российской Федерации. В работе демонстрируется стратегия построения интегрированного продукта, позволяющая превзойти фондовый рынок.
При формировании портфеля из финансовых активов инвестор чаще всего опирается на такие показатели, как доходность и риск. В портфельном анализе широкое применение нашли модели финансовых рынков, состоящих из рисковых и безрисковых активов. Данные модели были разработаны такими учеными, как Марковиц Г., Блек Ф., Линтнер Дж., Мертон Р., Миллер М., Шарп У., Модильяни Ф., Моссин Я., Тобин Д., Фабоцци Ф., Шоулз М.
Целью данной работы является построение интегрированного продукта, состоящего из фондового индекса, паевого инвестиционного фонда (ПИФ) и безрискового актива. Для достижения поставленной цели нужно выполнить следующие задачи:
1) анализ и отбор ПИФов на основе показателей ожидаемой доходности и индекса Дженсена;
2) выбор безрискового актива;
3) составление портфеля из ПИФа, безрискового актива и фондового индекса ММВБ.
В основе работы лежит классическая модель из рисковых и безрисковых активов, минимизирующая риск вложений при заданном уровне доходности:
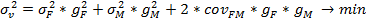
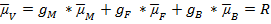
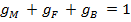
где M — индекс ММВБ, F- паевой фонд, B — безрисковый актив,
gM, gF, gB — доли активов M, Fи B в общем объеме вложений инвестора,
covFM — ковариация доходностей М и F
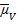, s2V — ожидаемая доходность и риск (дисперсия) вложений инвестора,
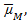
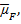
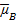— ожидаемые доходности активов M, F, B соответственно, R — константа.
В качестве фондового индекса (рыночного портфеля), паевого инвестиционного фонда и безрискового актива соответственно будут выступать индекс ММВБ, пай ВТБ — Фонд Телекоммуникаций и Альянс — государственных облигаций. Информационной базой послужил сайт Investfunds [1]. Данные представлены месячные на основе трехлетнего периода по 19 ноября 2013 года. Итак, безрисковая ставка доходности составляет 0,48 % в месяц (i=0,48), стандартное отклонение доходности рыночного портфеля равно 5,2 % (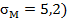
, ожидаемая доходность рыночного портфеля равна 9,53 % (
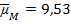), стандартное отклонение доходности пая равно 6,26 % (
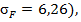коэффициент корреляции между доходностями рыночного портфеля и пая составляет 0,2 (ρ=0,2), отклонение между фактической ожидаемой доходностью пая и равновесной ожидаемой доходностью, вычисленной по модели CAPM (линия SML), равна 0,252 % (α=0,252), коэффициент чувствительности доходности пая к изменению доходности рыночного портфеля M составляет 0,875 (β=0,875), фактическая ожидаемая доходность предложенного пая равна 8,6 % 
.
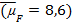Визуально исходные показатели можно представить графически (см. рис. 1 и 2). На рисунке 1 ось ординат — ожидаемая доходность (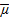
), ось абсцисс — коэффициент бета (β), β представляет собой коэффициент чувствительности доходности актива к изменению доходности рыночного портфеля (в нашем случае фондового индекса ММВБ). На рисунке 2 ось абсцисс — стандартное отклонение доходности актива (σ).
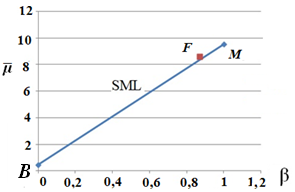
Рис. 1. Графическое изображение пая F относительно линии SML
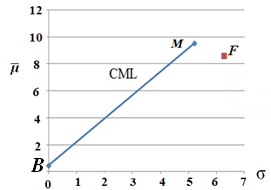
Рис. 2. Графическое изображение пая F относительно линии СML
На рисунках 1 и 2 показано положение финансового актива (пая) по отношению к линии доходности рынка ценных бумаг (SML) и к линии рынка капиталов (CML). Таким образом, пай является недооцененным (α>0, линия SML, см. рис.1), но является неэффективным (лежит ниже линии CML, см. рис.2). Все эффективные портфели, согласно модели CAPM, принадлежат линии CML. Поэтому рациональный инвестор не стал бы держать пай в качестве единственного наполнения своего портфеля, так как он не является эффективным. Однако, с помощью комбинирования пая с рыночным портфелем в определенных оптимальных соотношениях, можно достичь точек, лежащих выше линии рынка капитала CML. Для этого необходимо вначале объединить пай F и рыночный портфель M в единый портфель P (см. рис.3). С учетом коэффициента корреляции между M и F все возможные комбинации портфеля P лежат на дуге.
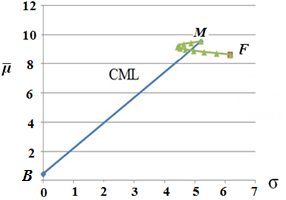
Рис. 3. Объединение пая F и рыночного портфеля M в единый портфель P
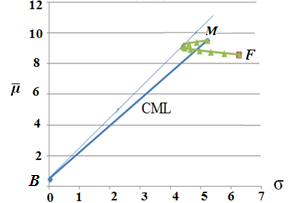
Рис. 4. Объединение портфеля Р и безрискового актива в портфель V
Затем необходимо объединить портфель Р и безрисковый актив B в портфель V. Получим интегрированный продукт. Все возможные комбинации составляющих данного интегрированного продукта (структура портфеля) лежат на линии, которая является касательной, проведенной из безрисковой ставки к портфелю, составленному из пая F и рыночного портфеля M (см. рис.4). На касательной лежат все возможные комбинации интегрированного продукта (см. рис.4).
Покажем, как отразятся предпочтения инвестора относительно доходности и риска на структуре портфеля V (интегрированного продукта).
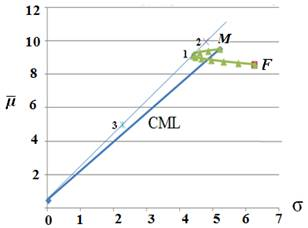
Рис. 5. Оптимальная структура вложений инвестора
На рисунке 5 изображены три различных структуры портфеля V. Структура портфеля V получается на основании расчетов по математической модели, описанной выше, задавая различное значение R. Расчеты можно произвести с помощью программного продукта MS Excel (Поиск решений).
Портфель 2 представляет собой случай, когда инвестор является заемщиком на рынке безрисковых активов (в этом случае доля безрискового актива отрицательна), т. е. будет привлекать дополнительные заемные средства в виде безрисковых активов по ставке процента i и размещать их в портфель P, составленный из F и M c доходностью выше, чем i, тем самым величина общего риска его вложений V превысит риск портфеля P. Структура портфеля 2: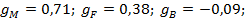 
ожидаемая доходность портфеля 2 равна 
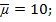риск, выраженный стандартным отклонением равен 
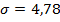(см. рис. 5).
Портфель 3 представляет собой случай, когда инвестор является кредитором на рынке безрисковых активов, т. е. его средства будут распределены между вложениями в портфель P из рисковых активов (F и M) и безрисковыми активами B, общий риск вложений V будет меньше, чем риск портфеля из рисковых активов P. Структура портфеля 3: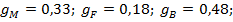 
ожидаемая доходность портфеля 3 равна 
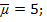риск, выраженный стандартным отклонением равен 
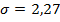(см. рис. 5).
Портфель 1 представляет собой случай, когда инвестор все свои средства вкладывает в портфель P, составленный только из рисковых активов F и M, следовательно, общий риск его вложений V будет равен риску этого портфеля (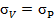
), т. к. в портфеле инвестора будут отсутствовать безрисковые активы. Структура портфеля 1: 
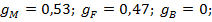ожидаемая доходность портфеля 1 равна 
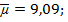риск, выраженный стандартным отклонением равен 
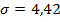(см. рис. 5).
В работе показан возможный вариант построения интегрированного продукта, состоящего из рисковых и безрисковых активов, учитывающий предпочтения инвестора относительно доходности и риска. Объединив пай, лежащий ниже линии CML, но выше линии SML, с рыночным портфелем и безрисковыми бумагами, получили комбинации, лежащие выше линии CML. Таким образом, данная стратегия позволила превзойти рынок.
Литература:
1. Investfunds [Электронный ресурс]. Электрон. дан. URL: http://pif.investfunds.ru (дата обращения: 25.11.13)
2. Зви Боди, Роберт Мертон. Финансы. — М.: Вильямс, 2007. С.592
