Статья посвящена вероятностному синтезу такой сложной механической системы как несущая конструкция главной балки металлургического мостового крана. В качестве входных параметров системы исследуются максимальные напряжения, возникающие в сечении несущей конструкции моста, а в качестве выходных — остаточная деформация и прогибы, возникающие при эксплуатации в мосте крана. Используется известный математический аппарат теории выбросов и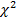 
— распределения Пирсона с выведенными формулами вероятностной взаимосвязи между входными и выходными параметрами. Материал статьи позволит принимать верные управленческие решения при обеспечении техногенной безопасности металлургических мостовых кранов, а также является существенным дополнением в теории вероятностного риск-анализа конструкций механических систем, оценки их надежности, долговечности и эффективности.
Ключевые слова:вероятностный синтез, механическая система, надежность, долговечность, упругопластическая деформация, несущая конструкция, металлургический кран, выходные и входные параметры системы, действующие нагрузки, напряжения, число выбросов, амплитуды нагрузок.
Введение. Большой интерес при вероятностном синтезе механических систем представляют задачи определения вероятности превышения случайной функцией, характеризующей процесс качественного изменения состояния материала конструкций, допустимых значений [1–13]. Это обусловлено, как представляется, недостаточной оценкой сложных механических систем различных производств, например таких, как несущие конструкции мостовых металлургических кранов. В механических системах среднее число выбросов амплитуд нагрузок за определенный промежуток времени мало и последовательность их появления все же можно считать независимыми редкими событиями.
Методика. Теоретическое обоснование и расчет надежности и долговечности сложной механической системы — несущей конструкции главной балки металлургического мостового крана грузоподъемностью 50 тонн осуществлены на основе вероятностного синтеза и теории выбросов.
Основная часть. Выбор этой механической системы обусловлен недостатками существующих методических указаний по обследованию металлургических кранов и так называемого принципа разумной надежности, проводимой в жизнь некоторыми руководителями предприятий, а именно, не проводить никаких мероприятий, пока не произойдет выход из строя конструкции. Такой подход имеет право на существование с учетом решения многих задач, в том числе прогнозирования долговечности на основе теории выбросов [2, 11].
Примем появление выбросов амплитуд нагрузки за допускаемый уровень приближенно подчиняющимся закону 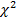— распределения Пирсона, тогда вероятность того, что для нормального стационарного процесса нагружения системы [2, 11] за время T случайная функция превысит уровень σ*, определится
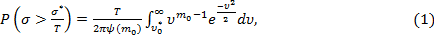
где σ* — случайная функция действующих нагрузок,
ν — параметр распределения Пирсона:
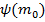— нормировочная постоянная распределения:
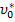— нижний предел интегрирования, представляющий минимальное значение распределения (2);
m0 — параметр распределения, представляющий собой показатель степени кривой усталости механической системы.
Исследуя процесс нагружения механической системы, будем рассматривать интеграл (1) в пределах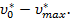 
Тогда (1) примет вид
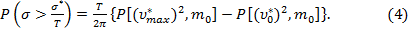
Таким образом, можно сформулировать последовательность оценки надежности и долговечности механической системы:
- интервал работы системы Т разбивается на несколько значений и по выражению (4) производится построение кривой надежности R = 1 — P. При этом необходимо иметь значения нагрузок на систему;
- устанавливается и анализируется зависимость между сроком службы и надежностью механической системы случайного процесса нагружения.
Рассматриваемой механической системой является кран грузоподъемностью 50 тонн, работающий в кислородно-конвертерном цехе металлургического предприятия 260 дней в году. Среднее число циклов совершаемых краном в две смены 600. Нормативный срок службы крана 15 лет. Общее количество циклов работы крана за весь его службы составит 2340000 циклов [1, 5, 6, 8, 9, 10,11]. Такому распределению нагрузок соответствует режим нагружения Q3 — тяжелый, Q4 — весьма тяжелый.
Результаты расчетов представим в виде графика изменения надежности выходных параметров механической системы на рисунке 1 по годам.
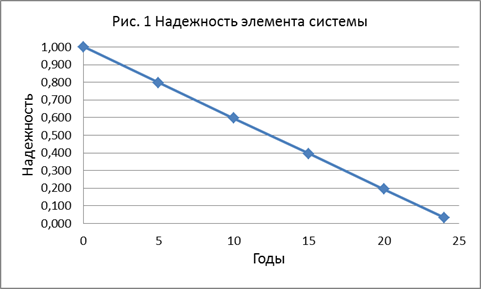
Рис. 1.
При полученных данных максимальная деформация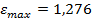 
в относительных единицах, а действующая нагрузка 
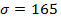МПа, рабочая деформация 
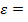0,786.
Выводы. Исследуя полученные расчетные и графические результаты случайного процесса на выходе сложной механической системы, можно определить все статистические характеристики распределения и решить задачу о сроке службы несущей конструкции моста металлургического крана. Видно, что при нормативном сроке службы крана 15 лет, работающего в тяжелых и сверхтяжелых условиях, расчеты позволяют принимать положительные решения о продлении его сроков службы или проведении дополнительного обслуживания или обследования, что существенно может повлиять на эффективность и безопасность производства.
Заключение. Таким образом, принимая допускаемый уровень действующих нагрузок рассматриваемой механической системы приближенно подчиняющимся закону 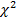— распределения Пирсона, можно определить вероятность нормального стационарного процесса нагружения. По результатам расчетов можно построить кривую надежности элементов сложной механической системы, по которой возможно будет судить о долговечности конструкции и сроках службы до следующего технического обслуживания или выхода из строя, что существенным образом может оказать влияние на ее характеристики как на стадии проектирования и построения, так и в процессе эксплуатации.
Литература:
1. Бархоткин В. В., Извеков Ю. А., Миникаев С. Р. Обзор аварий на крановом оборудовании металлургических производств. Международный журнал прикладных и фундаментальных исследований. — Москва, РАЕ, 2013. — № 10–1. С. 9–11.
2. Бирюков М. П. Динамика и прогнозирующий расчет механических систем. «Вышэйшая школа». — Минск, 1980. — 189 с: ил.
3. Извеков Ю. А. Анализ техногенной безопасности кранового хозяйства России. Современные наукоемкие технологии. — Москва, РАЕ, 2012. — № 12. С. 18–19.
4. Извеков Ю. А., Кобелькова Е. В., Лосева Н. А. Анализ динамики и вопросы оптимизации металлургических мостовых кранов. Фундаментальные исследования. — Москва, РАЕ, 2013. — № 6–2. С. 263–266.
5. Извеков Ю. А. Риск-анализ оборудования металлургических производств. Подход, концепция, анализ. Монография. — Saarbrucken, Deutschland. LAP Lambert, 2013. — 56 c.
6. Извеков Ю. А. Моделирование прогнозирования риска несущих конструкций кранов металлургического производства. Актуальные проблемы современной науки, техники и образования. — Магнитогорск, МГТУ, 2012. № 70, Т. 1. С. 6–8.
7. Извеков Ю. А., Кобелькова Е. В., Лосева Н. А. Аналитическая оценка пластической деформации несущих конструкций металлургических мостовых кранов. — Магнитогорск, МГТУ, 2013. № 71, Т. 1. С. 48–51.
8. Извеков Ю. А. Математическое моделирование оценки упругопластической деформации несущих конструкций механических систем. Современные тенденции в образовании и науке: сборник научных трудов по материалам Международной научно-практической конференции 31 октября 2013: в 26 частях. Часть 15; М-во обр. и науки. Тамбов: Изд-во ТРОО «Бизнес-Наука-Общество», 2013. С. 57–58.
9. Извеков Ю. А. Прогнозирование надежности несущих конструкций кранов металлургических производств. Вопросы. Гипотезы. Ответы: Наука XXI века: Коллективная монография. — Краснодар, 2013. Книга 6, часть 3, глава 9. С. 189–211.
10. Извеков Ю. А., Кузина Т. Г. Оценка упругопластической деформации на основе метода преобразования вероятностей. Современные проблемы науки и образования. — 2013. — № 6; URL: www.science-education.ru/113–10810 (дата обращения 14.02.2014).
11. Izvekov Y. A., Dubrovsky V. V., Hamutskikh E. Y. Mathematical Modeling and Calculation of Accuracy and Durability of Mechanical Systems' Elements. World Applied Sciences Journal 30 (1): pp. 32–34, 2014
12. Крылова Е. А., Извеков Ю. А. О подходе к оценке техногенной безопасности металлургического производства. Успехи современного естествознания. Москва, РАЕ, 2012. — № 6. С. 32–33.
13. Уляков М. С. Обоснование комбинированного способа подготовки к выемке блочного высокопрочного камня: диссертация на соискание ученой степени кандидата технических наук / Магнитогорский государственный технический университет им. Г. И. Носова. Магнитогорск, 2013. 152 с.
