К вопросу преподавания дисциплины «Спецглавы математики»

С введением новых образовательных стандартов на некоторых специальностях появилась новая дисциплина по выбору «Спецглавы математики». Дисциплина входит в естественнонаучный и математический цикл, являясь связующим звеном между курсами математической подготовки и общепрофессиональных дисциплин. В зависимости от направления подготовки студентов к ней относят различные разделы математики.

В частности, для студентов, обучающихся по направлению «Строительство», к «Спецглавы математики» отнесены дифференциальные уравнения. Главной целью изучения дисциплины является подготовка студентов к работе в области теории, практики и интерпретации инженерных и физических исследований с использованием дифференциальных уравнений. Безусловно, при изучении курса дифференциальных уравнений студентам необходимо сначала разъяснить основные методы их решения, а затем только применение при моделировании технологических процессов и обработки результатов экспериментов.

На простых примерах можно показать процедуру идентификации кинетических процессов формирования основных физико-механических характеристик строительных материалов. Известно, что обобщенная динамическая модель кинетических процессов является решением задачи Коши: 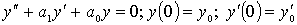, где 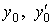 определяются видом исследуемого кинетического процесса.

Рассмотрим результаты исследования прочности лакокрасочных покрытий на пористой цементной подложке. Как показывает опыт, нельзя утверждать, что на разных этапах активной стадии накопления повреждений интенсивность изменения свойств покрытия одинакова, на графиках может наблюдаться несколько точек перегиба. В зависимости от вида покрытия и некоторых других причин первая половина активной стадии (средняя доля всей долговечности покрытия) характеризуется особенно резким увеличением всех негативных параметров, в дальнейшем процессы протекают более плавно. Предложим описать кинетику разрушения покрытий дифференциальными уравнениями порядка выше второго. Это означает, что при анализе процесса необходимо учитывать не только скорость изменения контролируемого параметра, но и как минимум ускорение. Рассматриваем в качестве модели процесса разрушения функцию 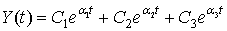, являющуюся решением дифференциального уравнения третьего порядка.

Коэффициенты 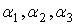 характеризуют скорость изменения контролируемого параметра на разных этапах старения покрытия.

Анализируя эмпирические кривые по кинетике накопления повреждений, можно принять, что 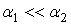(для площади поверхности покрытия характерно даже ), .

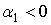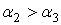В качестве примера рассмотрим изменение площади поверхности поливинилацетатцементного покрытия в процессе увлажнения.

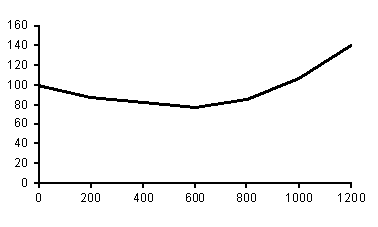
Рис.1. Изменение площади поверхности ПВАЦ покрытия в процессе старения

Из экспериментальных данных следует: ,,, .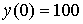

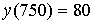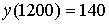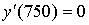Для идентификации параметров модели решаем систему уравнений

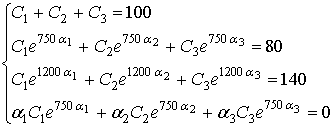
Из первых трех уравнений получим

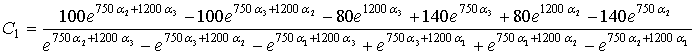
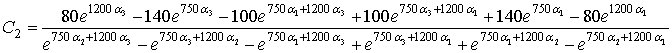
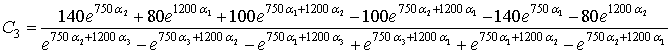
Определим 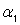 и 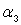 по экспериментальной характеристикеY(t) (рис. 1). Так как 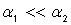, то составляющая  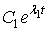определяет процесс до конца инкубационного периода, т. е. при 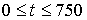. Значение  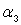можно определить по концу экспериментально полученного процессаY(t).

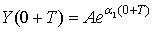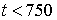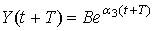А именно, , при , , при ,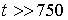

, .

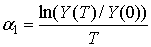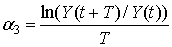В данном случае, , .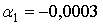

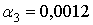Из четвертого уравнения системы (2) получим неявное выражение для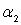

.

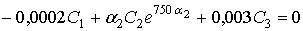Приближенное решение этого уравнения даст .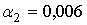

В результате решение исходного дифференциального уравнения представится в виде

.

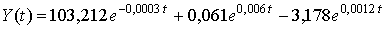Из изложенного выше вытекает следующий алгоритм идентификации кинетических процессов данного вида:

1)      По начальным изменениям инкубационного периода определяется 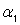, по концу эмпирической кривой — ;

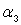2)      Константы С₁, С₂, С₃ представляются как функции от ;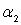

3)      По характерной точке эмпирической кривой строится уравнение (3), находится приближенное значение константы ;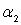

4)      Наконец, определяется .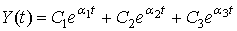

Предложенный алгоритм может быть использован при решении других задач строительного материаловедения с возможностью описания рассматриваемых процессов как решений дифференциальных уравнений третьего порядка.

Для студентов, обучающихся по направлению «Экономика», в дисциплину «Спецглавы математики» включены вопросы нелинейного программирования, динамического программирования, сетевые модели. Основная цель изучения данной дисциплины заключаются в обучении математическим методам, необходимым для анализа и моделирования экономических процессов и явлений, поиска оптимальных решений в сфере экономических проблем, выбора наилучшего способа реализации этих решений.

Модели динамического программирования применяются при разработке правил управления запасами, при распределении инвестиций между возможными направлениями их использования, разработке правил замены выбывающих из эксплуатации основных фондов и т. п. При решении задачи динамического программирования о распределении инвестиций между предприятиями процесс использования оборудования разбивается на n шагов. Управление на каждом шаге характеризуется качественными признаками и, как правило, состоит из двух возможных решений: продолжить эксплуатацию оборудования, с учетом издержек на поддержание его в рабочем состоянии, либо продать оборудование, бывшее в употреблении, и приобрести новое, которое уже в течение первого года эксплуатации потребует некоторых издержек на поддержание его в рабочем состоянии. Решение задачи проводится на графе, размещенном в системе координат. При решении задачи на нахождение оптимального плана замены оборудования на шестилетний период, если известны: прибыль от эксплуатации оборудования 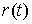 в зависимости от возраста; остаточная стоимость 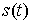оборудования в зависимости от возраста; стоимость нового оборудования 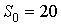на оси абсцисс откладывают номер шага (количество прошедших лет), на оси ординат — возраст оборудования на данный момент времени.

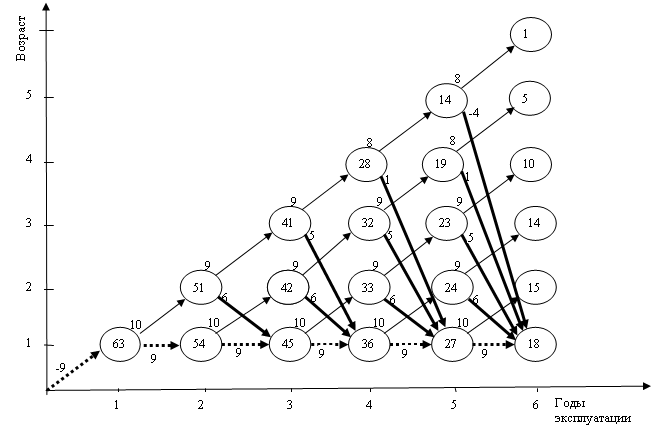
Перемещение на графе начинается из начала координат, что соответствует началу нового календарного года и началу эксплуатации нового оборудования. Переход по стрелке вверх означает решение о продолжении эксплуатации «старого» оборудования. Переход по стрелке вниз или горизонтально вправо означает решение о продаже «старого» оборудования, приобретении нового с последующей эксплуатацией в течение года нового оборудования. Над каждым соединением в графе записывают его характеристику, в данной задаче суммарную величину полученной прибыли.

Если стрелка идет вверх, то на прибыль влияют:доходы от эксплуатации оборудования в зависимости от его возраста на данный момент; его производительность; издержки на эксплуатацию оборудования в зависимости от его возраста на данный момент.

В данной задаче доходы и издержки уже согласованы и в исходной таблице указана прибыль, зависящая от возраста оборудования.

Если стрелка идет вниз или вправо, то на прибыль могут влиять: остаточная стоимость продаваемого «старого» оборудования; расходы на покупку нового оборудования; доходы от эксплуатации нового оборудования; издержки на эксплуатацию нового оборудования в течение первого года его эксплуатации.

Закончив маркировку стрелок, далее начинают обратный ход по графу, выясняя для каждого узла оптимальный переход (оптимальное решение). Причем маркировка узлов к началу обратного хода должна отсутствовать.

Рис. 2. Оптимальный план замены оборудования

Закончив заполнение графа, визуально по жирным стрелкам определяют траекторию оптимального перехода по всему периоду эксплуатации. В данном случае такая траектория единственная (рис. 2). Поскольку вся траектория состоит из стрелок вправо, нет ни одной стрелки вверх, делаем вывод о том, что выгоднее всего с точки зрения максимальной прибыли за шесть лет, обновлять оборудование каждый год.

Литература:

1.                  Куимова К. А., Куимова Е. И., Ячинова С. Н. Идентификация кинетических процессов // Вестник магистратуры, 2014. № 3(30). С.38–40.

2.                  Куимова Е. И., Куимова К. А., Ячинова С. Н. Формирование мотивационной составляющей обучения на примере изучения дифференциальных уравнений // Молодой ученый, 2014. № 2(61). С.775–777.

3.                  Логанина В. И., Днилов А. М., Куимова Е. И. Применение наследственной теории старения к прогнозированию стойкости строительных материалов. — Пенза, ПГУАС, 2003. 78с.