Существует много способов построения 3D моделей. Квалифицированные специалисты, обладающие большим опытом конструкторской работы, имеют собственные подходы к разработке твердотельных моделей, выработанные многолетней практикой. Часто этот опыт приобретается через совершение определенного количества проб и ошибок и не всегда, в итоге, приводит к наиболее рациональному решению.
При обучении студентов твердотельному моделированию перед преподавателем стоит задача не только дать навыки работы с графическими редакторами, но и выработать у них пространственное воображение, умение видеть в сложных формах составляющие их простые. Научить студентов выбирать и комбинировать различные способы построения 3D моделей — с использованием твердотельных примитивов, операций вращения, выдавливания, булевых операций и т. д.
Исходя из определения компьютерной графики как раздела информатики, который занимается проблемами получения различных изображений на компьютере [1], кажется целесообразным использовать в обучение такое базовое понятие информатики как алгоритм решения задачи.
Анализ литературных источников показал, что учебных пособий и методических указаний по построению моделей недостаточно, а имеющиеся не содержат оптимальных алгоритмов для создания 3D моделей деталей различной сложности. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма.
Для реализации этой задачи нужно проанализировать основные технические формы, сгруппировать их по алгоритму построения и создать базовые решения, которые могут быть положены в основу моделирования.
Одна из первых работ по 3D моделированию — построение твердотельной модели геометрического тела с вырезом (рис.1). Задача относится к проекционному черчению. Зачастую студенты даже плохо представляют себе форму модели, не говоря о том, чтобы выбрать построение с меньшим количеством операций.
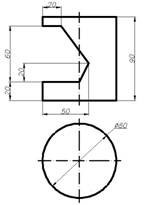
Рис. 1.
Нами был разработан алгоритм построения 3D модели с вырезом.
1. Создать рабочую среду (рис.2.):
- открыть AutoCAD;
- перейти в рабочее пространство 3D моделирования;
- переустановить лимиты пространства модели: координаты левого нижнего угла 0,0 и правого верхнего 100, 100;
- включить сетку;
- установить вид — ЮЗ изометрия;
- показать все поле чертежа.
- установить визуальный стиль — Реалистичный;
- создать слой с именем «Модель» и сделать его текущим.

Рис. 2.
2. Создать твердотельный примитив (цилиндр) (рис. 3):

Рис. 3.
3. Повернуть систему координат вокруг оси Х на 90 градусов (рис. 4).
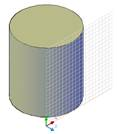
Рис. 4.
4. Построить контур выреза.
Для удобства построения использовать шаговую и объектную привязки (рис. 5).
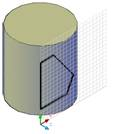
Рис. 5.
5. Преобразовать замкнутый контур в объект-область (рис. 6).

Рис. 6.
6. Командой Выдавить создать твердое тело, используя созданную область (рис.7).
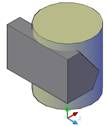
Рис. 7.
7. Вычесть созданное тело из цилиндра, используя команду Вычитание (рис. 8).
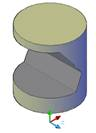
Рис. 8.
Занятие проводится следующим образом. Вначале студентам раздаются индивидуальные задания. Все они содержат однотипные модели. Это могут быть цилиндры с вырезом, как на представленном примере, а также конусы, пирамиды, призмы и сферы.
Затем преподаватель показывает построение, с использованием проектора, а студенты записывают алгоритм. После этого каждый выполняет свой вариант.
На базе полученного навыка построения, в дальнейшем, может быть предложен вариант, где модель имеет несколько вырезов, идущих в разных направлениях. Задача решается по тому же алгоритму, только пункты с третьего по седьмой повторяются в цикле.
Как показал опыт, при использовании алгоритма построения, время выполнения задания студентами значительно уменьшается. Их внимание не рассеивается, интерес сохраняется на протяжении всего занятия, так как они не тратят свои силы на бесконечные попытки, часто не приводящие к желаемому результату.
Алгоритмическая подача информации по построению, которая сопровождается иллюстрациями о том, что и на каком этапе происходит, не только облегчает процесс обучения, но и во многом помогает сформировать логический тип пространственного мышления.
Литература:
1. Абрамова, О. Ф. Компьютерная графика: конспект лекций для студентов направлений 230100.62 «Информатика и вычислительная техника» и 231000.62 «Программная инженерия» [Электронный ресурс]: учеб. пособие / Абрамова О. Ф.; ВПИ (филиал) ВолгГТУ // Учебные пособия: сб. Серия «Естественнонаучные и технические дисциплины». Вып. 3. — Волжский, 2012. — 165 с.
2. Безрукова, Т. В. Разработка 3D моделей резьбовых соединений / Безрукова Т. В., Мишустина С. Н., Асеева Е. Н., Мишустин О. А., Асеева С. Д. // Молодой учёный. — 2013. — № 12 (ч. 1). — C. 100–103.
3. Асеева, Е. Н. Визуализация образов средствами компьютерного твёрдотельного моделирования как способ решения геометрических задач / Асеева Е. Н., Авдеюк Д. Н., Асеева С. Д. // Инновации и современные технологии в системе образования: матер. III междунар. науч.-практ. конф., 20–21 февр. 2013 г. / НИЦ «Социосфера» [и др.]. — Прага, 2013. — С. 300–301.
4. Авдеюк, О. А. Совершенствование форм и методов преподавания дисциплин студентам первого курса при переходе к новым стандартам образования / Авдеюк О. А., Асеева Е. Н., Крохалев А. В. // Молодой учёный. — 2012. — № 5, ч. 3. — C. 387–389.
5. Асеева, Е. Н. Совершенствование форм и методов обучения графическим дисциплинам при переходе к государственным стандартам 3-го поколения / Асеева Е. Н., Авдеюк О. А. // Преподавание графических дисциплин в современных условиях: сб. науч. тр. 43-й межвуз. науч.-метод. конф. (24 июня 2013 г.) / Национальный исследовательский Томский политехн. ун-т. — Томск, 2013. — C. 8–13.
6. Асеева, Е. Н. Использование методологии структурного анализа и проектирования SADT/IDEF0 в планировании научно-исследовательской работы студентов / Асеева Е. Н., Авдеюк О. А., Асеева С. Д. // Инновационные информационные технологии: матер. первой междунар. науч.-практ. конф., г. Прага, 23–27 апр. 2012 г. / Моск. гос. ин-т электроники и математики (МИЭМ) [и др.]. — М., 2012. — C. 14–15.







