В квантовой теории поля встречаются интегральные операторы вида
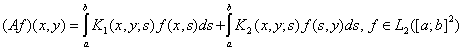 , (1)
, (1)
где 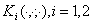 ограниченные функции на
ограниченные функции на 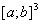 . В монографии К. О. Фридрихса [1] описана типичная ситуация, приводящая к операторам вида (1). Аналогичные операторы встречаются, например, в работах [2, 3, 4] и др. С другой стороны, изучение разрешимости частных интегральных уравнений вида
. В монографии К. О. Фридрихса [1] описана типичная ситуация, приводящая к операторам вида (1). Аналогичные операторы встречаются, например, в работах [2, 3, 4] и др. С другой стороны, изучение разрешимости частных интегральных уравнений вида 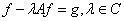 , в пространстве
, в пространстве 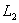 , где
, где 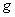 - заданная функция из
- заданная функция из 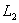 , является важным при исследовании спектра решетчатых гамильтонианов много частичной системы [5, 6] и интересным с математической точки зрения. Надо отметить, что в 1975 г. Л. М. Лихтарников и Л. З. Витова [7] впервые начали изучать спектральные свойства частично интегральных операторов. В работе [7] исследован спектр самосопряженного частично интегрального оператора с ядрами из гильбертово пространства
, является важным при исследовании спектра решетчатых гамильтонианов много частичной системы [5, 6] и интересным с математической точки зрения. Надо отметить, что в 1975 г. Л. М. Лихтарников и Л. З. Витова [7] впервые начали изучать спектральные свойства частично интегральных операторов. В работе [7] исследован спектр самосопряженного частично интегрального оператора с ядрами из гильбертово пространства 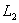 .
.
В данной работе подробно изучаются спектр и резольвента одного ограниченного самосопряженного частично интегрального оператора.
Рассмотрим частично интегральный оператор 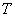 , заданный в гильбертовом пространстве
, заданный в гильбертовом пространстве 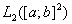 по правилу
по правилу
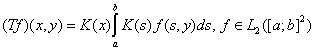 ,
,
где 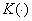 - вещественно значная непрерывная функция на
- вещественно значная непрерывная функция на 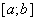 . Тогда оператор
. Тогда оператор 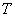 является ограниченным самосопряженным оператором в гильбертовом пространстве
является ограниченным самосопряженным оператором в гильбертовом пространстве 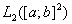 , причем
, причем
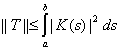 .
.
Всюду в работе через 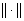 обозначена норма элемента из
обозначена норма элемента из 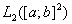 .
.
Следующая теорема описывает множество собственных значений оператора 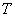 и их кратность.
и их кратность.
Теорема 1. Число 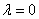 является бесконечнократным собственным значением оператора
является бесконечнократным собственным значением оператора 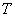 , а число
, а число 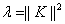 является его простым собственным значением.
является его простым собственным значением.
Доказательство. Сначала докажем 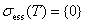 . Рассмотрим уравнение
. Рассмотрим уравнение 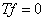 или
или
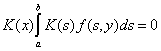 .
.
Видно, что функции вида 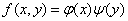 , где
, где 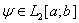 любая функция, а функция
любая функция, а функция 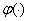 ортогональна к функции
ортогональна к функции 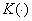 . Очевидно, что подпространство таких функций
. Очевидно, что подпространство таких функций 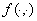 имеет размерность равный бесконечности. Поэтому число
имеет размерность равный бесконечности. Поэтому число 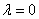 является бесконечнократным собственным значением оператора
является бесконечнократным собственным значением оператора 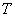 .
.
Пусть теперь 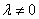 . Рассмотрим уравнение
. Рассмотрим уравнение 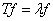 или
или
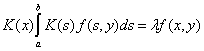 . (2)
. (2)
Так как 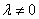 , из уравнения (2) для
, из уравнения (2) для 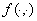 имеем
имеем
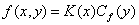 , (3)
, (3)
где

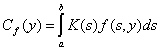 . (4)
. (4)
Подставляявыражение (3) для 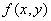 в равенству (4) получим, что уравнение (2) имеет ненулевое решение тогда и только тогда, когда
в равенству (4) получим, что уравнение (2) имеет ненулевое решение тогда и только тогда, когда
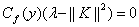 .
.
Если 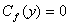 , то в силу равенства (3) имеем
, то в силу равенства (3) имеем 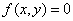 . Это противоречие показывает, что
. Это противоречие показывает, что 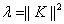 , т. е. число
, т. е. число 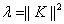 является собственным значением оператора
является собственным значением оператора 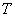 и соответствующая собственная функция имеет вид
и соответствующая собственная функция имеет вид 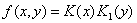 , где
, где 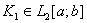 произвольная функция. Теорема 1 доказана.
произвольная функция. Теорема 1 доказана.
Таким образом имеет места равенства
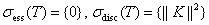 .
.
Теперь сформулируем результат о явном виде резольвенты оператора 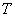 .
.
Теорема 2. При каждом фиксированном 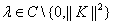 резольвента
резольвента 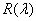 оператора
оператора 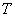 определяется следующим образом:
определяется следующим образом:
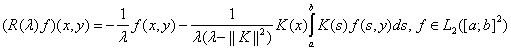 .
.
Доказательство. Пусть 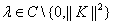 . Для построения резольвенты нам понадобится рассмотреть уравнение
. Для построения резольвенты нам понадобится рассмотреть уравнение 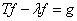 для любых
для любых 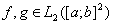 , т. е.
, т. е.
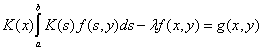 . (5)
. (5)
Так как 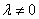 , из уравнения (5) для
, из уравнения (5) для 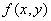 имеем
имеем
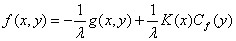 , (6)
, (6)
где 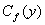 определен по формуле (4). Подставляя полученное выражение (6) для
определен по формуле (4). Подставляя полученное выражение (6) для 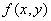 в равенству (3) имеем
в равенству (3) имеем
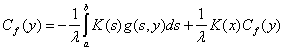
или
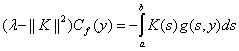 .
.
Учитывая соотношение 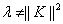 , для
, для 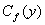 имеем
имеем
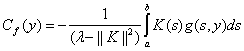
Далее, подставляя полученное выражение для 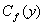 в равенство (6) приходим к равенству
в равенство (6) приходим к равенству 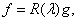 ,
, 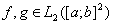 . Теорема 2 доказана.
. Теорема 2 доказана.
Литература:
1. К. О. Фридрихс. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир, 1972.
2. В. А. Какичев, Н. В. Коваленко. К теории двумерных интегральных уравнений с частными интегралами // Украинский математический журнал, 1973, Т. 25, № 3, С. 302–312.
3. J. Appell, E. V. Frolova, A. S. Kalitvin and P. P. Zabjenko. Partial integral operators on 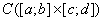 // Integral Equations and Operator Theory, 1997, V. 27, No. 2, P. 125–140.
// Integral Equations and Operator Theory, 1997, V. 27, No. 2, P. 125–140.
4. A. S. Kalitvin and P. P. Zabjenko. On the theory of partial integral operators // J. Integral Equations Appl., 1991, V. 3, No. 3, P. 351–382.
5. D. Mattis. The few-body problem in a lattice // Rev. Modern Phys., 1986, V. 58, No. 2, P. 361–379.
6. A. I. Mogilner. Hamiltonians in solid-state physics as multi-particle discrete Scroedinger operators: problems and results // Adv. Soviet Math., Providence, RI: Amer. Math. Soc., 1991, V. 5, P. 139–194.
7. Л. М. Лихтарников, Л. З. Витова. О спектре интегрального оператора с частными интегралами // Литовск. Матем. Сб., 1975, Т. 15, № 2, С. 41–47.







