Задача массового обслуживания заключается либо в формировании потока требований в систему, либо в обеспечении средствами обслуживания, либо в одновременном решении этих вопросов [1,2]. Целью решения этой общей задачи является минимизация суммарных затрат, связанных с ожиданием обслуживания требований и потерями от простоя средств обслуживания. Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы системы массового обслуживания (СМО) — число каналов, их производительность, характер потока заявок и т. п. — c показателями эффективности СМО (описывают способность справляться с потоком заявок). В качестве показателей эффективности СМО используются: среднее число заявок, обслуживаемых вединицу времени; среднее число заявок в очереди; среднее время ожидания обслуживания; вероятность отказа при обслуживании без ожидания; вероятность превышения числа заявок в очереди заданного значения и т. п.
Выделяются два основных класса СМО: сотказами и с ожиданием (очередью). В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, покидает СМО и в дальнейшем процессе обслуживания не участвует (например, заявка на телефонный разговор в момент, когда все каналы заняты, получает отказ и покидает СМО необслуженной). В СМО с ожиданием заявка, поступившая в момент, когда все каналы заняты, становится в очередь на обслуживание.
СМО с ожиданием могут отличаться друг от друга организацией очереди: сограниченной или неограниченной длиной очереди, с ограниченным временем ожидания и т. п.
Работу СМО можно рассматривать как случайный процесс. Если возможные события  этого процесса можно заранее перечислить, а переход системы из одного состояния в другое происходит мгновенно, то получим процесс с дискретным состоянием.
этого процесса можно заранее перечислить, а переход системы из одного состояния в другое происходит мгновенно, то получим процесс с дискретным состоянием.
Если моменты возможных переходов системы из состояния в состояние случайны, а не фиксированы заранее, то такой процесс есть процесс с непрерывным временем.
Случайный процесс является марковским или случайным процессом без последействий, если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t и не зависят от того, когда и как система пришла в это состояние. Анализ работы СМО существенно упрощается, если она описывается как марковский процесс.
Ограничимся рассмотрением устройства, состоящего из двух узлов, каждый из которых может выйти из строя в случайный момент; вышедший узел ремонтируется; время ремонта — неопределенное. Здесь возможны следующие состояния системы: S0 — оба узла исправны; S1–1-й узел ремонтируется, 2-й работает; S2–2-й ремонтируется, 1-й работает;
S3 — оба узла ремонтируются (рис.1).
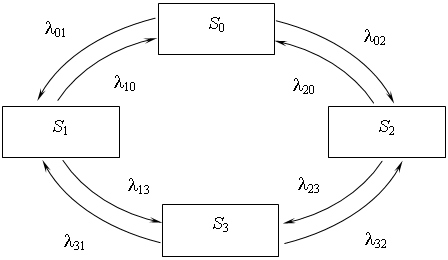 |
Рис. 1. Граф состояний системы
Переходы системы из состояния Siвсостояние Sjможно рассматривать как простейшие потоки с интенсивностями lij(i,j=0...3). Так, переход системы из состояния S0 в S1 происходит под воздействием потока отказов 1-го узла, а переход из состояния S1вS0 под воздействием потока «завершения ремонтов» 1-го узла. Назовем вероятностью i-го состояния вероятность 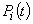 того, что в момент t система находится в состоянии Si. Для любого момента t справедливо
того, что в момент t система находится в состоянии Si. Для любого момента t справедливо 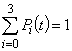 . Рассмотрим систему в момент t. Зададим малый промежуток времени h и найдем вероятность
. Рассмотрим систему в момент t. Зададим малый промежуток времени h и найдем вероятность 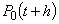 того, что система в момент t+h будет находиться в состоянии S0. Переход системы в состояние S0может осуществляться по-разному. Укажем возможные переходы.
того, что система в момент t+h будет находиться в состоянии S0. Переход системы в состояние S0может осуществляться по-разному. Укажем возможные переходы.
1. Система в момент t с вероятностью 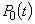 находилась в состоянии S0, а за время h не вышла из него. Из состояния S0 систему можно вывести суммарным простейшим потоком с интенсивностью
находилась в состоянии S0, а за время h не вышла из него. Из состояния S0 систему можно вывести суммарным простейшим потоком с интенсивностью 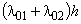 , а вероятность противоположного события, что система не выйдет из состояния S0, равна
, а вероятность противоположного события, что система не выйдет из состояния S0, равна 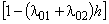 . В рассматриваемом случае вероятность того, что система будет находиться в состоянии S0, по теореме умножения вероятностей будет равна
. В рассматриваемом случае вероятность того, что система будет находиться в состоянии S0, по теореме умножения вероятностей будет равна 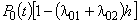 .
.
2. Система в момент t с вероятностью 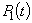 (или
(или 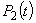 ) находилась в состоянии S1 (или S2) и за время h перешла в состояние S0. Потоком с интенсивностью
) находилась в состоянии S1 (или S2) и за время h перешла в состояние S0. Потоком с интенсивностью 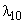 (или
(или 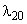 ) система перейдет в состояние S0 с вероятностью, приближенно равной
) система перейдет в состояние S0 с вероятностью, приближенно равной 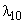 h (или
h (или 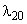 h). Здесь вероятность того, что система будет находиться в состоянии S0, равна
h). Здесь вероятность того, что система будет находиться в состоянии S0, равна 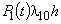 (или
(или 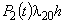 ).
).
По теореме сложения вероятностей:
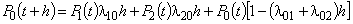 ;
;
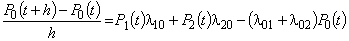 .
.
Переходя к пределу при 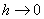 , получим
, получим 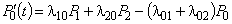 .
.
Аналогично определим вероятности 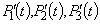 для других состояний системы. В результате получим систему дифференциальных уравнений Колмогорова для вероятностей состояний :
для других состояний системы. В результате получим систему дифференциальных уравнений Колмогорова для вероятностей состояний :
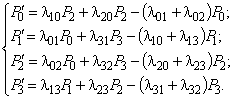 .
.
 Для простоты запоминания отметим, что в правой части каждого из уравнений стоит сумма произведений вероятностей всех состояний. На графе из них идут стрелки в данное состояние, на интенсивности соответствующих потоков, выводящих систему из данного состояния, умноженные на вероятности i-го состояния. В полученной системе уравнений независимых будет три. В качестве четвертого уравнения принимается очевидное равенство
Для простоты запоминания отметим, что в правой части каждого из уравнений стоит сумма произведений вероятностей всех состояний. На графе из них идут стрелки в данное состояние, на интенсивности соответствующих потоков, выводящих систему из данного состояния, умноженные на вероятности i-го состояния. В полученной системе уравнений независимых будет три. В качестве четвертого уравнения принимается очевидное равенство 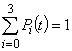 . Начальные условия имеют вид:
. Начальные условия имеют вид: 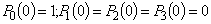 . Решив полученную задачу Коши, определим все вероятности состояний как функции времени.
. Решив полученную задачу Коши, определим все вероятности состояний как функции времени.
Аналогичную картину получим для любых систем с конечным числом состояний.
В предположении возможности перехода системы из каждого состояния в любое другое можно определить вероятности 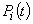 при
при 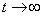 (предельные вероятности). Предельной вероятностью состояния Si определяется среднее относительное время пребывания системы в состоянии Si). Так как предельные вероятности постоянны, то для определения предельных вероятностей получим следующую систему линейных алгебраических уравнений, описывающую стационарный режим:
(предельные вероятности). Предельной вероятностью состояния Si определяется среднее относительное время пребывания системы в состоянии Si). Так как предельные вероятности постоянны, то для определения предельных вероятностей получим следующую систему линейных алгебраических уравнений, описывающую стационарный режим:
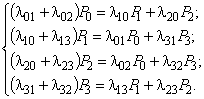
Так, если предельные состояния системы S при l01=1, l02=2, l10=2, l13=2, l20=3, l23=1, l31=3, l32=2, то система уравнений, описывающая стационарный режим (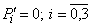 ), имеет вид:
), имеет вид:
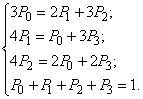
Решив ее, найдем: P0=0,40; Р1= 0,20; Р2=0,27; Р3=0,13. Откуда следует, что в предельном стационарном режиме система будет находиться в состоянии S0–40 %, S1–20 %, S2–27 %, S3–13 % времени.
Рассмотрим далее упорядоченное множество состояний системы S0, S1, S2, S3,..., Sn. Пусть переходы могут осуществляться из любого состояния Sk только в состояния с соседними номерами: Sk-1или Sk+1 (рис.2).
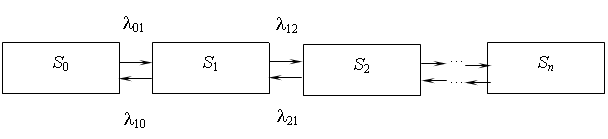 |
Рис. 2. Граф состояний
Пусть далее все потоки событий, соответствующие переходам системы по стрелкам графа, являются простейшими с интенсивностями lk,k+1 или lk+1,k. По графу составим алгебраические уравнения для предельных вероятностей. Для состояния S1справедливо: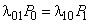 . Для S2:
. Для S2: 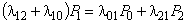 . С учетом приведенного равенства для S1 отсюда получим
. С учетом приведенного равенства для S1 отсюда получим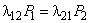 .
.
Аналогично определятся уравнения и для других состояний. Окончательно для определения предельных вероятностей 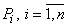 получим следующую систему алгебраических уравнений:
получим следующую систему алгебраических уравнений:
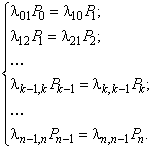 .
.
Добавив к этой системе уравнение 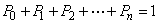 и решив ее, получим:
и решив ее, получим:
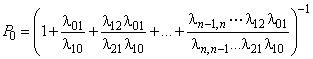 , (1)
, (1)
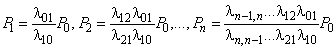 .
.
В формулах для P1, P2,...,Pn коэффициенты при P0 есть слагаемые, стоящие после 1 в формуле (1). Числители этих коэффициентов представляют собой произведения всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния Sk, а знаменатели — произведения всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния Sk.
Рассматриваемый подход эффективно использовался при анализе управляющих воздействий оператора транспортной эргатической системы как поток импульсов [3…5].
Литература:
1. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
2. Будылина Е. А., Гарькина И. А., Данилов А. М. Декомпозиция динамических систем в приложениях / Региональная архитектура и строительство. –2013. — № 3. — С. 95–100.
3. Гарькина И. А., Данилов А. М., Петренко В. О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. № 2(41). 2013. –С.123–130.
4. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. –2013. –№ 5. –С. 42–45.
5. Гарькина И. А., Данилов А. М., Домке Э. Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). –2011. –№ 2. –С. 18–23.







