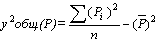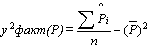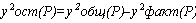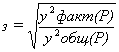Подтверждается гипотеза о наличии влияния размера среднедушевого дохода населения и количества заключаемых браков на уровень рождаемости в Российской Федерации.
Ключевые слова: регрессионный анализ, корреляционный анализ, рождаемость, доход, брак.
В современной России существует достаточно широкий круг социально-экономических проблем, которые можно отнести к глобальным. Это и высокий уровень безработицы, сравнительно низкие заработные платы и, конечно же, низкий уровень рождаемости, что в итоге приводит к естественной убыли населения, являющейся одной из основных причин других социально важных проблем, влияющих на развитие экономической системы России. Для решения этой сложнейшей задачи Правительство Российской Федерации с 1 января 2007 года утвердило программу «Материнский капитал», которая позволяет получать средства на второго, третьего и последующих детей в качестве дополнительной поддержки со стороны государства. Данное мероприятие призвано к изменению негативных тенденций, связанных с убылью населения. Принятое решение способствует росту рождаемости, однако естественного прироста не наблюдается.
Целью настоящего исследования является подтверждение гипотезы о наличии влияния размера среднедушевого дохода населения и количества заключаемых браков на уровень рождаемости в Российской Федерации. Данные показатели находятся в постоянной взаимной и всеохватывающей объективной связи. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами очень важно, оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования интенсивности, вида и формы зависимостей широко применяется корреляционно-регрессионный анализ, который является методическим инструментарием при решении задач прогнозирования, планирования и анализа.
Для построения модели оценки влияния размера среднедушевого дохода населения и количества заключаемых браков на уровень рождаемости в Российской Федерации использованы статистические данные, представленные в табл. 1. [4, 5]
Таблица 1
Исходные данные для проведения многофакторного анализа
|
Период |
Рождаемость, чел. (Р) |
Браки, шт. (Б) |
Среднедушевой доход, руб. (СД) |
|
2003г. |
1477301 |
1091778 |
5167,4 |
|
2004г. |
1502477 |
979667 |
6399,0 |
|
2005г. |
1457376 |
1066366 |
8088,3 |
|
2006г. |
1479637 |
1113562 |
10154,8 |
|
2007г. |
1610122 |
1262500 |
12540,2 |
|
2008г. |
1713947 |
1179007 |
14863,6 |
|
2009г. |
1761687 |
1199446 |
16895,0 |
|
2010г. |
1788948 |
1215066 |
18958,4 |
|
2011г. |
1796629 |
1316011 |
20780,0 |
|
2012г. |
1902084 |
1213598 |
23058,0 |
В табл. 1 представлены значения исследуемых показателей, среди которых Р — рождаемость является результирующим фактором, а фактор времени, количество браков и среднедушевой доход являются влияющими. Данные представлены в динамике, что позволит сделать анализ более достоверным. Для большей точности прогноза значения рождаемости были сглажены по пяти точкам.
Необходимым условием осуществления последовательных расчетных операций при построении модели оценки влияния размера среднедушевого дохода населения и количества заключаемых браков на уровень рождаемости является предварительное определение наличия или отсутствия тренда в динамическом ряду параметров, характеризующем уровни рождаемости в каждом из обозначенных периодов в России. Выявление тенденции основывается на использовании метода проверки разностей средних уровней. Для этого динамический ряд разбивается на две равные по числу уровней части (n1=5 и n2=5). По каждой из частей рассчитаны средние значения уровней динамического ряда и исправленные дисперсии. Расчетные значения обозначенных показателей представлены в табл. 3.
Таблица 3
Результаты расчетов средних значений показателей динамического ряда и исправленных дисперсий
|
1 часть ряда |
2 часть ряда |
||
|
Среднее значение ( |
Исправленная дисперсия ( |
Среднее значение ( |
Исправленная дисперсия ( |
|
1520115,56 |
3484366853,77 |
1781295,32 |
6512983789,87 |
После проверяется гипотеза о равенстве дисперсий 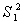 и
и 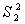 этих совокупностей на основе F-критерия Фишера. Сравнение расчетного значения критерия с табличным критическим при уровне погрешности 5 % и степенями свободы k1=4 (k1=n1–1) и k2=4(k2=n2–1) показало наличие тренда. Окончательная проверка гипотезы о наличии тренда произведена с использованием t-критерия Стьюдента. [2. 3] Расчетное значение t-критерия больше табличного, то есть тренд существует. Расчетные значения обозначенных критериев представлены в табл. 4.
этих совокупностей на основе F-критерия Фишера. Сравнение расчетного значения критерия с табличным критическим при уровне погрешности 5 % и степенями свободы k1=4 (k1=n1–1) и k2=4(k2=n2–1) показало наличие тренда. Окончательная проверка гипотезы о наличии тренда произведена с использованием t-критерия Стьюдента. [2. 3] Расчетное значение t-критерия больше табличного, то есть тренд существует. Расчетные значения обозначенных критериев представлены в табл. 4.
Таблица 4
Значения F-критерия Фишера и t-критерия Стьюдента
|
Критерий Фишера |
Критерий Стьюдента |
||
|
Fрасч |
Fтабл |
tрасч |
tтабл |
|
1,869201512 |
6,39 |
33865,45311 |
2,31 |
Следующим этапом анализа является выявление вида зависимости исследуемых факторов. Для этого используется метод характеристик прироста, вследствие чего выявлено, что зависимость является логарифмической, и уравнение имеет следующий вид:
lgP=lga0+Б*lga1+СД*lga2+t*lga3 (1)
где P — уровень рождаемости;
Б — количество браков;
СД — среднедушевой доход населения;
a0, a1, a2, a3— параметры;
t — вбирает в себя все неучтенные факторы, меняющие свое значение от периода к периоду.
Аналитическое выравнивание статистических данных по методу наименьших квадратов предполагает нахождение такого теоретического уровня, который удовлетворял бы следующим условиям: сумма линейных отклонений теоретических значений ряда от статистических равна нулю; сумма квадратов этих отклонений есть величина наименьшая.
Неизвестные параметры a0, a1, a2, a3 вычисляются методом наименьших квадратов посредством системы линейных уравнений:
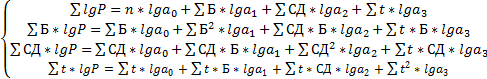 (2)
(2)
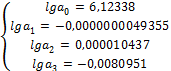 (3)
(3)
Искомое уравнение зависимости примет следующий вид:
lgP=6,12338 — Б*0,0000000049355 + СД*0,000010437 — t*0,0080951 (4)
Чем меньше разность между фактическими значениями уровня рождаемости (P) и теоретически ожидаемыми (), найденными с помощью уравнения модели, тем яснее выражена закономерность связи между признаками. Поэтому при определении параметров a0, a1, a2, a3 важно обеспечить минимум отклонений (P — ). Поскольку отклонения имеют разные знаки, необходимо, чтобы минимальной была сумма квадратов отклонений. В этом состоит сущность метода наименьших квадратов. Анализ результатов расчета отклонений показывает, что расхождение между значениями существующего и теоретически ожидаемого уровня удовлетворенности потребителей услуг не превышает 1 %.
Далее произведём оценку стандартной ошибки:
S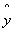 =
= 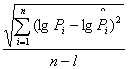 , S
, S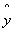 = 0,274 (5)
= 0,274 (5)
Малая величина ошибки в отклонениях между практическими и теоретическими значениями критериальной переменной свидетельствует о надежности найденной закономерности и возможности ее использования для решения практических задач.
Для определения степени влияния размера среднедушевого дохода населения и количества заключаемых браков на уровень рождаемости в Российской Федерации и тесноты связи между показателями воспользуемся показателями общей, факторной, остаточной дисперсии и коэффициентом тесноты связи. [2. 3] Результаты расчетов представлены в табл. 5.
Таблица 5
Оценка влияния размера среднедушевого дохода населения и количества заключаемых браков на уровень рождаемости в Российской Федерации и тесноты связи между показателями
|
Показатель |
Расчетная формула |
Значение показателя |
|
Общая дисперсиярезультативного признака P, отображающая совокупное влияние всех факторов |
|
0,001451029 |
|
Факторная дисперсия, отображающая вариацию результативного признакаPтолько от воздействия изучаемых факторов Б, СД |
|
0,001446539 |
|
Остаточная дисперсия, отображающая вариацию результативного признака P от всех прочих, кроме Б, СД факторов |
|
0,0000044906 |
|
Коэффициент тесноты связи результативного признака P и изучаемых факторов Б, СД |
|
0,998451413 |
Анализ данных таблицы позволяет сделать следующий вывод: из общей величины дисперсии уровня рождаемости на долю факторной приходится 99,85 %, между результативным признаком и изучаемым фактором существует тесная связь.
Таким образом, на основе методических принципов осуществления корреляционно-регрессионного анализа и моделирования выявлена зависимость уровня рождаемости в Российской Федерации от размера среднедушевого дохода населения и количества заключаемых браков, построена модель, которая учитывает высокую степень зависимости критериальной переменной от регрессоров и может быть использована для получения достоверного вариативного прогноза уровня рождаемости.
Литература:
1. Дубина, И. Н. Математико-статистические методы в эмпирических социально-экономических исследованиях [Текст]: учеб. пособие по дисц. «Эконометрика» для вузов по направл. «Экономика» / И. Н. Дубина. — М.: Финансы и статистика [и др.], 2010. — 414 с.
2. Кузнецова Л. В. Методические аспекты моделирования оценки влияния состояния этапов процесса управления обслуживанием на уровень обслуживания потребителей предприятий сферы услуг // Вестник ИНЖЭКОНа. Серия: Экономика. — 2010. — № 1. — с. 352–355.
3. Нечипоренко Л. В. Оценка влияния уровня удовлетворенности производителей на уровень удовлетворенности потребителей услуг // Вестник Поволжского государственного университета сервиса. Серия: Экономика. — 2013. — № 5 (31). — с. 64–68.
4. Федеральная служба государственной статистики. Население. [Электронный ресурс]. — Режим доступа: http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/population/demography/#. Дата обращения 25.05.2014.
5. Федеральная служба государственной статистики. Уровень жизни. [Электронный ресурс]. — Режим доступа: http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/population/level/#. Дата обращения 25.05.2014.







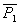 )
)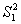 )
)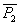 )
)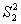 )
)