Введение
Оптимизация алгоритма часто сводится к поиску компромисса между временем работы алгоритма и размером требуемой памяти. Так в [1] представлен способ оптимизации алгоритма Нидлмана-Вунша для выравнивания биологических последовательностей на GPU. Суть оптимизации заключалась в переупорядочивании элементов матрицы динамического программирования так, чтобы вычислимые одновременно элементы матрицы находились в одной строке. В этом случае производится объединение транзакций в глобальной памяти [2], что ускоряет работу программы. Однако размер глобальной памяти, которая требуется программе, в два раза больше, чем у неоптимизированного алгоритма.
В данной статье предложена дальнейшая модификация алгоритма, уменьшающая количество требуемой глобальной памяти при том же времени работы.
Постановка задачи
Недостатком алгоритма, предложенного в [1], является то, что часть глобальной памяти остается неиспользованной. Так на рис. 1 показана схема размещения элементов матрицы для последовательностей длины 5.
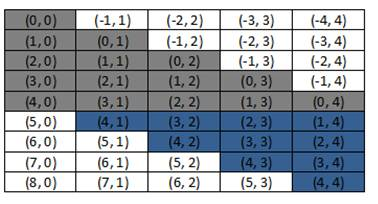
Рис. 1. Размещение элементов матрицы
Не закрашенные ячейки не используются, что приводит к увеличению требуемой памяти.
Если перенести элементы матрицы из нижнего правого угла в верхний правый (рис. 2), то можно сэкономить глобальную память GPU.
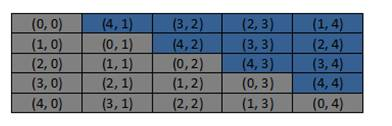
Рис. 2. Оптимальное размещение элементов матрицы
Если длины последовательностей различны, то перенос элементов матрицы производится в несколько шагов (рис 3).

Рис. 3. Размещение элементов матрицы для последовательностей разной длины
Таким образом мы избавились от неиспользуемых элементов матрицы.
Нумерация элементов матрицы
В [1] предложена нумерация 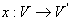 , где
, где 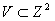 и
и 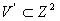 , приводящая к ускорению работы алгоритма:
, приводящая к ускорению работы алгоритма:
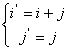 (1)
(1)
И обратная 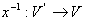 :
:
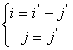 (2)
(2)
Для того чтобы привести матрицу к виду, представленному на рис. 2 и рис. 3, необходимо модифицировать данную нумерацию. Так прямая нумерация 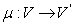 примет вид:
примет вид:
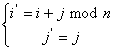 (3)
(3)
где n число строк матрицы.
А обратная нумерация 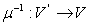 :
:
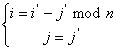 (4)
(4)
где n число строк матрицы.
В результате применения нумерации µ каждый столбец исходной матрицы циклически сдвигается вниз на один элемент относительно предыдущего. Размеры новой и исходной матриц совпадают.
Реализация алгоритмов
Рассмотрим различные реализации алгоритма Нидлмана-Вунша на GPU на языке CUDA:
- без применения нуменации;
- с использованием нумерации n по формулам (1), (2);
- с использованием нумерации µ по формулам (3), (4).
При использовании нумерации µ будет использоваться блочная схема разделения данных, предложенная в [3].
Так например для последовательностей из 16-и элементов и размером блока 4x4 схема вычисления для нумерации n представлена на рис 4.
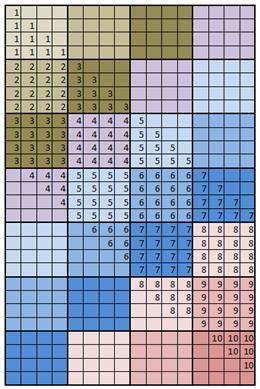
Рис. 4. Блочная схема вычислений для нумерации n
Элементы матрицы, обозначенные одинаковыми числами, вычисляются в одном блоке. Эти же числа задают последовательность вычисления блоков.
Для нумерации µ для аналогичных последовательностей схема вычисления представлена на рис. 5.
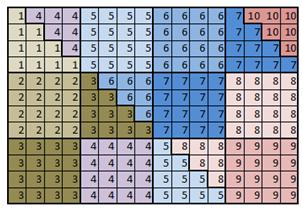
Рис. 5. Блочная схема вычислений для нумерации µ
Отличие схемы на рис. 5 от схемы на рис. 4 состоит в том, что блоки с нижней части матрицы перенесены наверх в неиспользуемую область матрицы.
Исходный код программы расположен в git-репозитории по адресу https://bitbucket.org/apotapoff/sequence_alignment.git версия 0.0.2. Эксперименты проведены на платформе NVIDIA GeForce GTX 460.
Каждая реализация алгоритма протестирована на последовательностях длины от 1000 до 10000 элементов и с размерами блоков 32x32, 64x64, 128x128, 256x256, 512x512 и 1024x1024 и измерено время заполнения матрицы. Результаты экспериментов представлены в таблице 1.
Таблица 1
Время выполнения алгоритмов
|
Размер блока |
Алгоритм |
Длина последовательностей |
|||||||||
|
1000 |
2000 |
3000 |
4000 |
5000 |
6000 |
7000 |
8000 |
9000 |
10000 |
||
|
32x32 |
Выравнивание без использования нумерации |
8,3712 |
18,4347 |
30,9772 |
45,8349 |
61,2395 |
82,1539 |
94,956 |
118,3299 |
142,6382 |
181,023 |
|
Выравнивание с использованием нумерации n |
9,33325 |
18,1817 |
27,5174 |
39,4621 |
57,1387 |
79,4344 |
96,0183 |
117,9722 |
135,2933 |
155,9577 |
|
|
Выравнивание с использованием нумерации µ |
9,82419 |
18,6697 |
29,377 |
49,2293 |
60,5969 |
70,7179 |
88,5577 |
122,0549 |
129,1574 |
155,7901 |
|
|
64x64 |
Выравнивание без использования нумерации |
6,89418 |
14,2774 |
22,9008 |
35,2036 |
48,7423 |
65,1388 |
84,8804 |
103,8087 |
127,22 |
156,6418 |
|
Выравнивание с использованием нумерации n |
6,98912 |
14,969 |
22,2287 |
25,6844 |
39,4222 |
46,1984 |
57,2349 |
66,70441 |
79,49523 |
94,69482 |
|
|
Выравнивание с использованием нумерации µ |
7,48467 |
14,8368 |
22,2213 |
29,8307 |
32,6881 |
45,7126 |
57,7186 |
66,60397 |
77,01539 |
85,10468 |
|
|
128x128 |
Выравнивание без использования нумерации |
6,21581 |
12,3179 |
21,7103 |
31,4886 |
45,7309 |
58,7854 |
77,2844 |
91,48333 |
116,2619 |
143,7531 |
|
Выравнивание с использованием нумерации n |
5,08643 |
10,6223 |
16,6522 |
22,6257 |
29,8924 |
34,2265 |
42,2107 |
47,52855 |
55,81709 |
58,34173 |
|
|
Выравнивание с использованием нумерации µ |
5,1735 |
11,2118 |
18,4742 |
21,1042 |
30,1705 |
37,444 |
43,7846 |
44,5624 |
58,73603 |
64,36906 |
|
|
256x256 |
Выравнивание без использования нумерации |
5,56592 |
11,7875 |
21,0461 |
30,0129 |
42,8015 |
63,934 |
75,6757 |
94,7992 |
119,7921 |
145,0101 |
|
Выравнивание с использованием нумерации n |
4,25488 |
8,98576 |
15,1808 |
20,1031 |
26,8714 |
30,4856 |
39,7563 |
45,40947 |
51,53875 |
59,04519 |
|
|
Выравнивание с использованием нумерации µ |
4,44026 |
9,91936 |
15,1893 |
20,6339 |
27,1128 |
32,9592 |
39,9499 |
47,29366 |
54,44983 |
63,02502 |
|
|
512x512 |
Выравнивание без использования нумерации |
5,3792 |
12,5781 |
21,3721 |
32,0174 |
46,2787 |
63,6912 |
79,5167 |
103,8639 |
122,853 |
149,8 |
|
Выравнивание с использованием нумерации n |
3,3527 |
8,57875 |
13,7461 |
18,6938 |
24,361 |
30,0921 |
36,3259 |
42,96586 |
50,64294 |
56,97511 |
|
|
Выравнивание с использованием нумерации µ |
3,46211 |
8,72835 |
13,996 |
19,137 |
24,8375 |
30,5568 |
37,0175 |
44,82311 |
52,96701 |
58,70816 |
|
|
1024x1024 |
Выравнивание без использования нумерации |
5,11574 |
15,3661 |
25,5704 |
36,4705 |
49,7379 |
66,8765 |
81,0235 |
112,3431 |
127,6924 |
156,7283 |
|
Выравнивание с использованием нумерации n |
2,86726 |
9,00042 |
16,0762 |
23,1439 |
30,3935 |
37,3335 |
44,3848 |
51,38403 |
59,10727 |
65,04784 |
|
|
Выравнивание с использованием нумерации µ |
2,82058 |
8,93277 |
15,9438 |
23,1269 |
30,0854 |
37,2775 |
44,3712 |
50,97421 |
65,58711 |
65,78848 |
|
Время заполнения матрицы для блока 256x256 различными реализациями алгоритма показано на рис. 6.
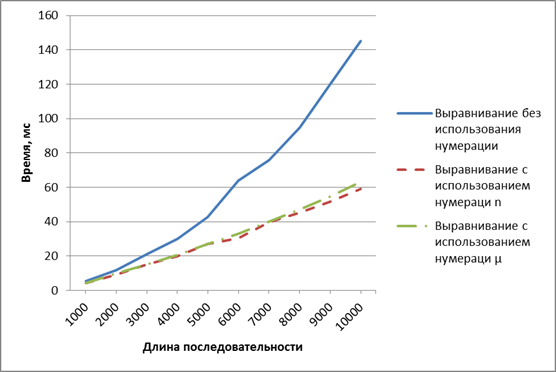
Рис. 6. Время работы алгоритмов для размера блока 256x256
Время работы алгоритмов с различными типами нумерации примерно одинаковое. Однако, при использовании нумерации µ размер требуемой глобальной памяти такой же как и без использования нумерации. Это позволяет обойти ограничение нумерации n на размер глобальной памяти GPU.
Вывод
В статье рассмотрен способ переупорядочивания элементов матрицы с помощью нумерации, позволяющий оптимизировать обращение к глобальной памяти GPU, посредством объединения транзакций. При этом не требуется выделения дополнительной памяти для матрицы. Проведены эксперименты, доказывающие, что использование нумерации ускоряет работу алгоритма.
Литература:
1. Потапов А. Н. Оптимизация алгоритма выравнивания биологических последовательностей на GPU [Текст] / А. Н. Потапов, Е. А. Кольчугина // Молодой ученый. — 2014. — № 3. — С. 75–83
2. Боресков А. В. «Параллельные вычисления на GPU. Архитектура и программная модель CUDA: учеб. пособие» — М.: Издательство Московского университета, 2012–336 с.
3. S. Che, M. Boyer, J. Meng, D. Tarjan, J. W. Sheaffer, and K.Skadron. A performance study of general-purpose applications on graphics processors using cuda. [Online]. Available:http://citeseerx.ist.psu.edu/viewdoc/summary?oi=10.1.1.143.4849







