Рассмотрим частный случай задачи нелинейного программирования, а именно квадратичного программирования [1,2], в которой минимизируется сумма линейной и квадратичной форм при ограничениях вида линейных неравенств при неотрицательности переменных. Эти соотношения имеют вид:
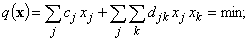
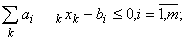
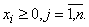 (1)
(1)
Ограничимся случаем, когда квадратичная форма является положительно определённой (а значит, и выпуклой; функция 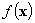 является выпуклой, если при любом 0 £ l £ 1 справедливо
является выпуклой, если при любом 0 £ l £ 1 справедливо
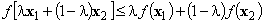
Линейная форма — также выпуклая функция. Поэтому целевая функция будет выпуклой. В этом случае необходимые условия Куна-Таккера являются и достаточными условиями существования единственного оптимума.
Для записи условий Куна-Таккера введём в рассмотрение функцию Лагранжа:
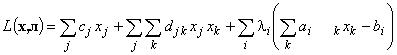 .
.
Производные от 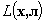 по xj и liзапишутся в виде
по xj и liзапишутся в виде
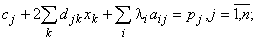
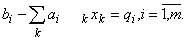 (2)
(2)
Условиями Куна-Таккера требуется найти решение этих уравнений при удовлетворении требований
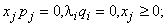
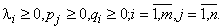 (3)
(3)
Отметим, что классическая задача оптимизации состоит в нахождении минимума целевой функции 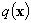 , где
, где 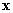 = (x1, x2,..., xn) — точка в пространстве
= (x1, x2,..., xn) — точка в пространстве 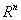 при наличии ограничений типа равенств
при наличии ограничений типа равенств
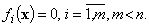
Если ограничения имеют место, то минимум функции 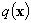 будет условным. Если ограничения отсутствуют, то говорят о безусловном минимуме, нахождение которого сводится к определению и исследованию стационарных точек функции
будет условным. Если ограничения отсутствуют, то говорят о безусловном минимуме, нахождение которого сводится к определению и исследованию стационарных точек функции 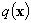 .
.
Классический способ решения данной задачи состоит в том, что уравнения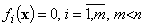 , используются для исключения из рассмотрения m переменных. При этом целевая функция приводится к виду
, используются для исключения из рассмотрения m переменных. При этом целевая функция приводится к виду
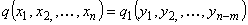 .
.
где через 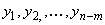 обозначены неисключённые переменные. Задача сводится к нахождению значений
обозначены неисключённые переменные. Задача сводится к нахождению значений 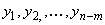 , которые обращают в минимум функцию q1 и на которые не наложено никаких ограничений, то есть к задаче на безусловный экстремум.
, которые обращают в минимум функцию q1 и на которые не наложено никаких ограничений, то есть к задаче на безусловный экстремум.
Если ограничения имеют сложный вид, то исключение с их помощью m переменных из функции 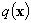 представляет значительные трудности. В связи с этим задачи на условный экстремум и сводятся к задаче на безусловный экстремум с использованием функции Лагранжа.
представляет значительные трудности. В связи с этим задачи на условный экстремум и сводятся к задаче на безусловный экстремум с использованием функции Лагранжа.
В рассматриваемом случае система (2) содержит 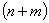 уравнений с
уравнений с 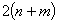 переменными
переменными 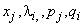 , из которых
, из которых 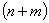 являются свободными и могут быть приравнены к нулю. Остальные переменные образуют при этом базисное решение, которое является допустимым, если выполняются условия (3).
являются свободными и могут быть приравнены к нулю. Остальные переменные образуют при этом базисное решение, которое является допустимым, если выполняются условия (3).
Если число переменных в задаче не велико, то можно попытаться угадать допустимое базисное решение, положив 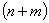 произвольных переменных свободными, приравняв их нулю, и, решив систему (3), найти значения базисных переменных. Однако нет никаких гарантий, что полученные значения переменных будут удовлетворять условиям (3). Поэтому попытки угадать допустимое базисное решение приходится проводить многократно.
произвольных переменных свободными, приравняв их нулю, и, решив систему (3), найти значения базисных переменных. Однако нет никаких гарантий, что полученные значения переменных будут удовлетворять условиям (3). Поэтому попытки угадать допустимое базисное решение приходится проводить многократно.
Если допустимое базисное решение найдено, то его улучшение, то есть переход к новому лучшему базису, производят на основании симплекс-метода, аналогично задаче линейного программирования. Отличие здесь заключается в том, что при выборе новой базисной переменной необходимо проверять выполнение условий 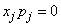 ,
, 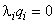 , которые означают, что если в базисе имеется
, которые означают, что если в базисе имеется 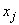 или
или 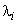 , то в него не может быть введено
, то в него не может быть введено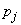 или
или 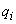 соответственно.
соответственно.
При большом числе переменных угадывание допустимого базисного решения становится чрезвычайно трудоёмким. В этом случае можно использовать эффективные известные систематические методы получения допустимого базисного решения.
Для иллюстрации рассмотрим задачу определения рецептурно-технологических параметров композита, при которых достигается максимальное значение прочности на сжатие 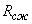 (эквивалентна минимизации
(эквивалентна минимизации 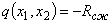 ). Предварительно с использованием методов математического планирования эксперимента была получена аппроксимационная модель
). Предварительно с использованием методов математического планирования эксперимента была получена аппроксимационная модель
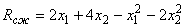
в области факторного пространства, удовлетворяющей условиям
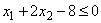 ,
,
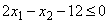 ,
,
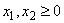
Функция 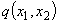 является выпуклой (представляет собой сумму линейной функции
является выпуклой (представляет собой сумму линейной функции 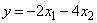 , которую можно рассматривать как выпуклую, и квадратичной формы
, которую можно рассматривать как выпуклую, и квадратичной формы 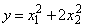 , которая является положительно-определенной и, следовательно, также выпуклой). Система ограничений задачи включает только линейные неравенства. Тогда можно воспользоваться теоремой Куна-Таккера. Составим функцию Лагранжа
, которая является положительно-определенной и, следовательно, также выпуклой). Система ограничений задачи включает только линейные неравенства. Тогда можно воспользоваться теоремой Куна-Таккера. Составим функцию Лагранжа
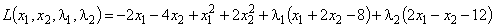
и запишем необходимые и достаточные условия существования седловой точки построенной функции:
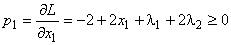 ,
,
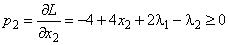 ;
;
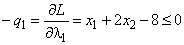 ,
,
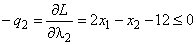 . (4)
. (4)
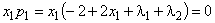 ,
,
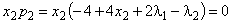 ;
;
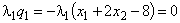 ,
,
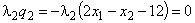 . (5)
. (5)
Введя дополнительные неотрицательные переменные 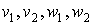 , обращающие неравенства (4) в равенства, получим:
, обращающие неравенства (4) в равенства, получим:
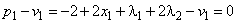 ,
,
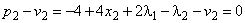 ;
;
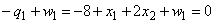 ,
,
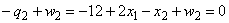 . (6)
. (6)
Седловая точка функции Лагранжа для исходной задачи будет получена (определено оптимальное решение), если будет найдено базисное решение системы линейных уравнений (6) с учетом выполнения равенств (5). Из (6) следует:
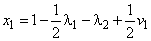 ,
,
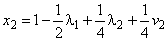 ;
;
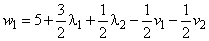 ,
,
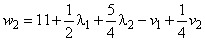 . (7)
. (7)
Тогда базисное решение будет иметь вид:
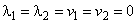 ,
,
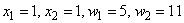 .
.
Здесь
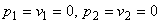 ;
;
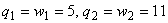 .
.
Справедливы условия
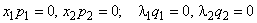 ,
,
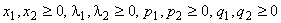 .
.
Так что
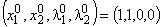
является седловой точкой функции Лагранжа для исходной задачи; 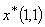 — оптимальный план исходной задачи;
— оптимальный план исходной задачи; 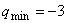 ;
; 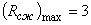 .
.
Использование условий Куна-Таккера оказалось эффективным и в ряде других случаев, связанных с синтезом композиционных материалов со специальными свойствами, а также с задачами управления в эргатических системах [3…7].
Литература:
1. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
2. Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление: монография. — Пенза: ПГУАС. — 2011. — 308 с.
3. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.
4. Будылина Е. А.,Гарькина И. А., Данилов А. М. Декомпозиция динамических систем в приложениях / Региональная архитектура и строительство.– 2013. — № 3(17). — C. 95–100.
5. Гарькина И. А., Данилов А. М., Домке Э. Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник МАДИ. — 2009. — № 2(17). — С.77–82.
6. Данилов А. М., Гарькина И. А. Методология проектирования сложных систем при разработке материалов специального назначения / Известия ВУЗов. Строительство.– 2011. — № 1. — С.80–85
7. Будылина Е. А., Гарькина И. А., Данилов А. М., Сухов Я. И. Некоторые подходы к анализу и синтезу сложных систем / Молодой ученый. — 2013. — № 10(57). — С.105–107.







