Рассматривается алгоритм расчета полей перемещений и скоростей, возбуждаемых контактной границей при различных граничных условиях. В частности рассмотрены два предельных случая взаимодействия полное прилипания и свободного проскальзывания.
Ключевые слова: контактная задача, удар, упругая среда, соударения, алгоритм, переходной процесс.
An algorithm for calculating fields of displacements and velocities, excited by the contact boundary under various boundary conditions. In particular considering two limit cases of interaction full adhesion and free slippage.
Keywords:contact problem, stroke, elastic medium, collision algorithm, the process of transition.
Рассматривается динамическая задача прямого удара бесконечного цилиндрического тело о жесткое полупространство. Пусть упругое тело, имеющее в сечении форму полукольца с внутренным радиусом 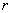 0 и внешним
0 и внешним 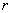 м, движется в направлении, перпендикулярном образующей, с постоянной скоростью V0 и ударяется о жесткое полупространство.
м, движется в направлении, перпендикулярном образующей, с постоянной скоростью V0 и ударяется о жесткое полупространство.
Предполагается, что в декартовой системе координат (х1,х2, х3), связанной с телом, ось х3 направлена вдоль оси цилиндра, а направление вектора скорости совпадает с осью симметрии х1 и нормально к поверхности преграды. Требуется определить параметры движения при условии, что известны геометрические и физические законы состояния и при различных допущениях относительно характера взаимодействия тел в процессе соударения.
В работе [1] приводится постановка осесимметричной динамической задачи о численном моделировании переходного процесса при ударе цилиндрического тела о жесткую преграду и приводятся некоторые результаты расчетов поведения упруго тела с учетом выхода переднего фронта волны за зону контакта.
В силу постановки задачи движение точек тела достаточно рассматривать в плоскости х3=const, ограниченной следующими линиями:
I. 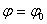 ,
, 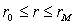 ;
;
II. 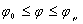 ,
,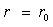 ;
;
III. 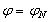 ,
, 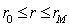 ;
;
IV. 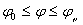 ,
, 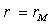 .
.
Алгоритм расчета пространственной задачи основан на лагранжевых конечных элементах [2]. Для более точной аппроксимации области тела конечно-элементная модель(расчетная область) строится в цилиндрической системе координат, а для более точного удовлетворения граничных условий переход из цилиндрической системы координат в декартовую осуществляется по формулам:
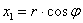 ,
, 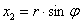
Внутри каждого элемента составляющие неизвестных функций перемещений представляются в виде разложения
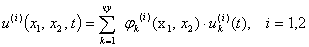 (1)
(1)
где 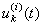 — узловые значения составляющих перемещений;
— узловые значения составляющих перемещений;
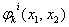 — специальным образом подобранные функции координат со следующими свойствами:
— специальным образом подобранные функции координат со следующими свойствами:

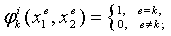
чy — число узлов в элементе.
Из (1) могут быть получены выражения для компонент скоростей и производных от перемещений по пространственным переменным, по которым нетрудно определить напряженно-деформированные состояния, используя следующие соотношения деформационной теории:
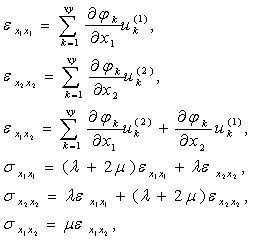
где
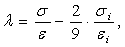
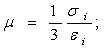
функции, связывающие инварианты тензоров напряжений и деформаций -
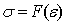 и
и 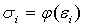 ,
,
определяются экспериментально.
Далее предполагается, что масса, непрерывно распределенная в элементе,
сосредотачивается в его узлах с весом 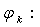
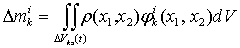 ,
,
где 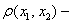 плотность среды в элементe;
плотность среды в элементe;
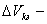 объем элемента;
объем элемента;
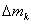 - доля общей массы элемента, сосредоточенная в его
- доля общей массы элемента, сосредоточенная в его 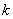 - м узле.
- м узле.
Уравнения движения выводятся на основе вариационного принципа Гамильтона-Остроградского и имеют следующий вид:
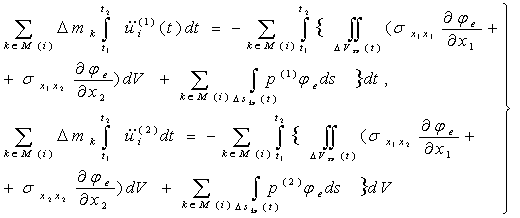 (2)
(2)
Здесь 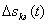 — площадь поверхности элемента,
— площадь поверхности элемента,
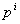 -заданные составляющие поверхностных сил,
-заданные составляющие поверхностных сил,
М( )-множество кратных элементов в узле с номером-
)-множество кратных элементов в узле с номером- 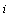 ,
,
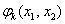 — функции формы,
— функции формы,
е — локальный номер узла i в k — м элементe.
Система уравнений в форме (2) описывает движение дискретной модели сплошной среды. Для того, чтобы уравнение (2) можно было применить к расчету разрывных движений компоненты тензора упругих напряжений заменяются величинами, учитывающими искусственную вязкость:
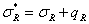
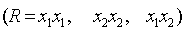 ,
,
где 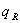 — компоненты псевдовязкостных напряжений.
— компоненты псевдовязкостных напряжений.
При решении конкретных задач удобно считать, что деформируемое тело до удара находится в покое, а жесткая преграда налетает на него со скоростью - . В зоне контакта рассмотрены два типа условий взаимодействия:
. В зоне контакта рассмотрены два типа условий взаимодействия:
1) полное прилипание и 2) отсутствие трения. В обоих случаях границы II,III и часть IY вне зоны контакта считаются свободными от усилий, а на границе I, в силу осевой симметрии, граничные условия определяются соотношениями
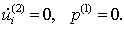
В первом случаю в зоне контакта известны значения скоростей:
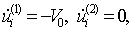
где i принимает все значения множества граничных узлов k(i), которые имеются в зоне контакта.
Уравнения движения i-го узла зоны контакта интегрируются с момента 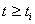 (времени подхода узла к преграде) при начальных значениях перемещений, соответствующих этому моменту:
(времени подхода узла к преграде) при начальных значениях перемещений, соответствующих этому моменту:
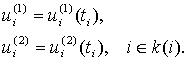
Во втором случае, когда точки поверхности могут свободно проскальзывать вдоль преграды, известны значения
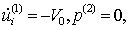
где 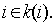
Система интегрируется численно с нулевыми начальными условиями и с шагом 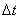 при предположении постоянства скоростей на каждом временном интервале.
при предположении постоянства скоростей на каждом временном интервале.
По вычисленным значениям ускорений из уравнений движения (2) определяются значения скоростей в момент времени 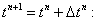

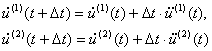
Эти значения скоростей приводят к изменению местоположения узлов:
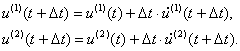
Как известно, применяемая схема условно устойчива, т. е. устойчива при соблюдении некоторых ограничений на шаг по времени. Это ограничение определяется условием Куранта, согласно которому за один временной интервал возмущение не может распространяться на расстояние более одного пространственного интервала
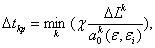 где
где 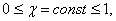 (3)
(3)
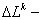 минимальный размер
минимальный размер 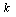 -го элемента,
-го элемента,
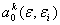
 -скорость звука в
-скорость звука в 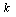 -м конечном элементе
-м конечном элементе
(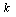 принимает значения номеров конечных элементов в возмущенной области).
принимает значения номеров конечных элементов в возмущенной области).
Интегрирование системы (2) с шагом (3) приводит к неточному определению момента попадания узла в зону контакта. Это обстоятельство требует при определении шага интегрирования учитывать взаимное расположение узлов поверхности тела и преграды.
Предполагается, что нормальная к преграде составляющая скорости 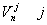 -го узла границы контакта в пределах каждого временного интервала (3) постоянна. Тогда из соотношения
-го узла границы контакта в пределах каждого временного интервала (3) постоянна. Тогда из соотношения 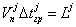 можно определить шаг
можно определить шаг
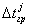 , т. е. время, необходимое для того, чтобы j-й узел попал в зону контакта.
, т. е. время, необходимое для того, чтобы j-й узел попал в зону контакта.
Здесь 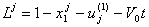 -расстояние в момент времени t oт j –го узла границы до преграды;
-расстояние в момент времени t oт j –го узла границы до преграды; 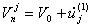 скорость сближения. Очевидно, что контакт для узла j может иметь место только при
скорость сближения. Очевидно, что контакт для узла j может иметь место только при 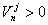 . Итак, из всех вычисленных
. Итак, из всех вычисленных 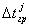 определяется один допустимый шаг:
определяется один допустимый шаг:
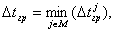
где М-множество узлов внешней границы тела вне зоны контакта.
Окончательно расчетный шаг определяется из соотношения
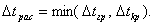
Такой выбор шага интегрирования позволяет, как показывают расчеты, с достаточной степенью точности установить момент попадания граничного узла в зону контакта. Расчет задачи проводился при механических и геометрических параметрах, заданых в безразмерной форме:
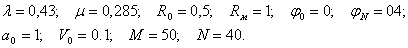
Расчетная область представляла собой 2000 четырехугольных элементов с 2050 узлами.
Как показывают расчеты, закон изменения зоны контакта на рассмотренном промежутке времени не зависит от характера взамодействия тела и преграды. Две кривые 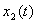 , соответствующие полному прилипанию и отсутствию трения, практически совпадают. Скорость расширения зоны контакта изменяется от бесконечного значения в начальный момент удара до некоторого стационарного значения при
, соответствующие полному прилипанию и отсутствию трения, практически совпадают. Скорость расширения зоны контакта изменяется от бесконечного значения в начальный момент удара до некоторого стационарного значения при 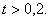 Кривая
Кривая 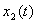 на промежутке времени, когда имеет место сверхзвуковой режим расширения зоны контакта, практически сливается с осью симметрии.
на промежутке времени, когда имеет место сверхзвуковой режим расширения зоны контакта, практически сливается с осью симметрии.
Из графиков изменения компонент напряжений видно, что в начальный момент времени напряжения на оси возрастают скачком, интенсивность которого со временем падает.
Графики изменения скорости 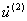 на границе IV для различных моментов времени в случае отсутствия трения с увеличением времени показывает сложную картину взаимодействия прямой и отраженной от свободной поверхности части границы IV волн.
на границе IV для различных моментов времени в случае отсутствия трения с увеличением времени показывает сложную картину взаимодействия прямой и отраженной от свободной поверхности части границы IV волн.
Анализ результатов показывают, что в начальный момент времени точки зоны контакта движутся к оси симметрии, а затем от оси. При этом крайняя точка зоны контакта является точкой разрыва тангенциальной составляющей скорости перемещений.
Литература:
1. Салиев Э.А, Савурбоев А., Тошпулатов М.А., Кувондиков Ж.Т. // Численное моделирование и исследование переходных процессов при высокоскоростном ударе цилиндрического тела о жесткую преграду. Молодой ученый. № 6(53).июнь, 2013г. с.138–142.
2. Зенкевич О. Метод конечных элементов в технике. М.,”Мир”,1975.







