Решена задача об образовании газогидрата в природном пласте, насыщенном газом и водой, в результате нагнетания газа. Получены численные решения плоскоодномерной задачи, описывающие распределения основных параметров в пласте. Исследовано влияние проницаемости пласта, а также давления нагнетаемого газа на особенности протекания процесса. Показано, что в зависимости от параметров нагнетаемого газа образование газогидрата может происходить как на фронтальной поверхности, так и в протяженной области.
Ключевые слова: газогидраты, пористая среда, фильтрация, гидратообразование.
Многие технологические процессы в нефтегазовой отрасли сопровождаются образованием и отложением газовых гидратов, как в пласте, так и в системах подземного и наземного оборудования нефтяных и газовых месторождений [1]. В настоящее время в большинстве случаев гидратообразование носит чаще негативный характер, связанный с аварийными остановками из–за «склероза» установок и последующими затратами на устранение таких осложнений. Однако процессы гидратообразования могут иметь и положительный аспект, например, использованы для увеличения емкости подземных резервуаров для хранения углеводородного газа [2]. Такая возможность обусловлена резким ростом массового содержания газа в газогидратном состоянии в единице объема по сравнению со свободным состоянием при той же температуре и давлении [3].
В данной работе в плоскоодномерном приближении рассматриваются некоторые особенности образования гидрата принагнетании газа в пористый пласт, заполненный в исходном состоянии газом и водой.
1. Постановка задачи
Пусть полубесконечный пористый пласт в начальный момент времени насыщен газом и водой, давление и температура которых в исходном состоянии соответствуют термодинамическим условиям существования их в свободном состоянии. Положим, что через границу пласта закачивается такой же газ, причем его давление и температура соответствуют условиям образования газогидрата и поддерживаются на границе области постоянными. При постановке данной задачи будем полагать, что в результате закачки газа от границы в глубь пласта начинает распространяться фронтальная поверхность образования гидрата, разделяющая пласт на две области. В первой области, находящейся вблизи границы пласта, вода полностью перешла в газогидратное состояние, поэтому в порах присутствуют только газ и газогидрат, а во второй (дальней) области поры заполнены газом и водой. Таким образом, согласно данной модели полагается, что образование газогидрата полностью происходит на фронтальной границе между этими двумя зонами.
2. Основные уравнения
При описании происходящих процессов тепломассопереноса примем следующие допущения: скелет пористой среды, газогидрат и вода несжимаемы и неподвижны, пористость постоянна, температура пористой среды и насыщающего вещества (газа, гидрата или воды) совпадают. Гидрат является двухкомпонентной системой с массовой концентрацией газа g.
В рамках принятых допущений уравнение сохранения массы газа имеет вид:
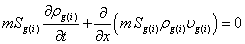 , (1)
, (1)
где m — пористость, Sg(i) — газонасыщенность. Здесь и далее нижние индексы sk, h, l, g относятся к скелету, гидрату, воде и газу соответственно; параметры первой и второй областей будут снабжены нижними индексами в скобках i = 1, 2.
В качестве закона фильтрации газа примем закон Дарси:
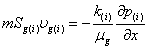 , (2)
, (2)
где k(i) — коэффициент проницаемости для газа, 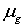 — динамическая вязкость газа.
— динамическая вязкость газа.
Зависимость коэффициента проницаемости для газа от газонасыщенности зададим на основе формулы Козени:
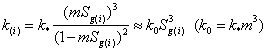 .
.
Газ будем считать калорически совершенным:
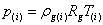 . (3)
. (3)
Уравнение притока тепла, пренебрегая баротермическим эффектом, запишем в виде:
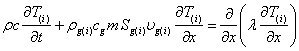 , (4)
, (4)
Здесь 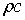 и
и 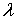 — удельная объемная теплоемкость и коэффициент теплопроводности системы. Поскольку в значения
— удельная объемная теплоемкость и коэффициент теплопроводности системы. Поскольку в значения 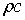 и
и 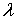 основной вклад вносят параметры скелета пористой среды, то во всем пласте будем полагать их постоянными.
основной вклад вносят параметры скелета пористой среды, то во всем пласте будем полагать их постоянными.
Данные уравнения необходимо дополнить условиями баланса массы и тепла на границе фазового перехода (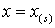 ) [4]:
) [4]:
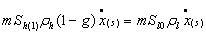
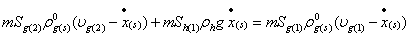 ,
,
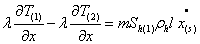 , (5)
, (5)
где Sh(1) — гидратонасыщенность первой области, Sl0 — начальная водонасыщенность, l — удельная теплота гидратообразования, 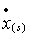 – скорость движения границы фазового перехода (нижний индекс s в скобках относится к параметрам на границе гидратообразования).
– скорость движения границы фазового перехода (нижний индекс s в скобках относится к параметрам на границе гидратообразования).
На границе между областями для температуры и давления выполняется условие фазового равновесия [5]:
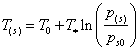 ,
,
где T0 — исходная температура системы, ps0 — равновесное давление, соответствующее исходной температуре, 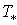 — эмпирический параметр, зависящий от вида газогидрата.
— эмпирический параметр, зависящий от вида газогидрата.
Будем полагать, что в начальный момент времени в пористой среде давление p0 и температура T0 во всех точках пласта одинаковы, причем 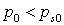 . Эти два условия запишем в виде:
. Эти два условия запишем в виде:
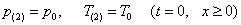 .
.
На границе гидратообразования потребуем условие непрерывности давления и температуры:
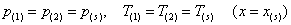 .
.
Условия на границе пласта запишем в виде:
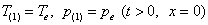 .
.
3. Результаты численных расчетов
Сформулированная выше задача является автомодельной. Введем автомодельную переменную 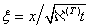 , где
, где 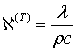 — коэффициент температуропроводности.
— коэффициент температуропроводности.
Тогда в автомодельных переменных можно получить решения, описывающие распределение температуры и давление в пласте.
На рис. 1, a представлены распределение температуры и давления при нагнетании метана под давлением pe= 5 МПа с температурой Te= 278 К в пласт с начальным давлением и исходной водонасыщенностью Sl0= 0,2. Для остальных параметров, характеризующих систему, приняты следующие значения: m= 0,1, g= 0,12, T0= 280 К, T* = 10 К, ps0= 5,5 МПа, 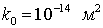 ,
, 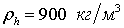 ,
, 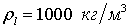 ,
, 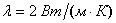 ,
, 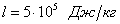 ,
, 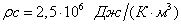 ,
, 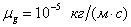 ,
, 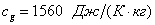 . Пунктирная линия 2 показывает равновесную температуру, соответствующую полученному распределению давления.
. Пунктирная линия 2 показывает равновесную температуру, соответствующую полученному распределению давления.
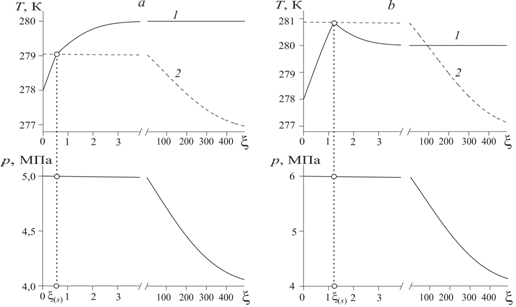
Рис. 1. Распределение температуры пласта (1), равновесной температуры (2) и давления: a — непротиворечивый случай, pe = 5 МПа, Te = 278 К; b — случай переохлаждения воды за фронтом, pe = 6 МПа, Te = 278 К.
Из данного рисунка видно, что температура пласта перед фронтом гидратообразования ниже равновесной температуры, а за фронтом — выше этой температуры. Следовательно, в этом случае решение с фронтальной поверхностью образования гидрата является непротиворечивым.
На рис. 1, b приведены распределение температуры и давления при нагнетании метана под давлением pe= 6 МПа с температурой Te= 278 К. В соответствии с рисунком температура пласта за фронтом гидратообразования опускается ниже равновесной температуры (пунктирная линия 2), что соответствует переохлаждению воды в этой области. Следовательно, в этом случае модель с фронтальной поверхностью образования гидрата не позволяет построить физически непротиворечивое решение.
По результатам численных расчетов можно сделать вывод о том, что возможны два принципиально различных вида решения в зависимости от параметров нагнетаемого газа. Также при различных значениях параметров, характеризующих систему, для величины давления, под которым нагнетается газ, существует некоторое максимальное значение, зависящее от проницаемости и исходной температуры, при превышении которого невозможно в рамках данной модели построить непротиворечивое решение. Для значений проницаемости, характерных для реальных пластов 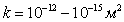 , величина этого предельного давления с высокой степенью точности совпадает с величиной равновесного давления ps0, соответствующего исходной температуре. Следовательно, модель с фронтальной поверхностью образования гидрата физически непротиворечиво описывает процесс только в случае закачки газа под давлением, не превышающим величину равновесного давления, соответствующего исходной температуре.
, величина этого предельного давления с высокой степенью точности совпадает с величиной равновесного давления ps0, соответствующего исходной температуре. Следовательно, модель с фронтальной поверхностью образования гидрата физически непротиворечиво описывает процесс только в случае закачки газа под давлением, не превышающим величину равновесного давления, соответствующего исходной температуре.
Литература:
1. Шагапов В. Ш., Хасанов М. К. Мусакаев Н. Г. Образование газогидрата в пористом резервуаре, частично насыщенном водой, при инжекции холодного газа // Прикладная механика и техническая физика. — 2008. — Т 49, № 3. — С.462–472.
2. Хасанов М. К., Столповский М. В., Кильдибаева С. Р. Численное моделирование образования газогидрата в пористой среде при инжекции газа // Вестник Башкирского университета. — 2013. — Т. 18. № 4. — С. 969–972.
3. Шагапов В. Ш., Хасанов М. К., Гималтдинов И. К., Столповский М. В. Численное моделирование образования газогидрата в пористой среде конечной протяженности при продувке газом // Прикладная механика и техническая физика. — 2011. — Т. 52, № 4. — С.116– 126.
4. Шагапов В. Ш., Хасанов М. К., Гималтдинов И. К., Столповский М. В. Особенности разложения газовых гидратов в пористых средах при нагнетании теплого газа // Теплофизика и аэромеханика. — 2013. — Т. 20, № 3. — С. 347–354
5. Гималтдинов И. К., Мусакаев Н. Г., Хасанов М. К., Столповский М. В. Особенности разложения газовых гидратов при тепловом и депрессионном воздействиях в пластах конечной протяженности // Вестник Тюменского государственного университета. — 2011.– № 7. — С. 6–13.







