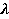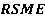Гибкие нейро-нечеткие системы вывода и программная реализация для решения задач аппроксимации

Нейро-нечеткие системы объединяют в себе достоинства нейронных сетей и классических нечетких систем. В отличие от нейронных сетей, нейро-нечеткие системы характеризуются четким представлением знаний, содержащихся в нечетких правилах. Также нейро-нечеткие сети можно обучать с помощью метода обратного распространения ошибки (основа обучения многослойных нейронных сетей) и эволюционных алгоритмов. Обучению чаще всего подвергаются параметры функций принадлежности суждений (компонент ЕСЛИ...) и заключений (компонент ТО...) нечетких правил. Перечисленные достоинства нейро-нечетких систем обусловили их широкое применение для решения задач моделирования, аппроксимации и классификации. В большинстве таких систем используется вывод типа Мамдани или логического типа.

Способ вывода (Мамдани или логический) может быть определен в процессе обучения. Такие системы называются гибкими нейро-нечеткими системами. Структура гибких систем изменяется в процессе обучения.

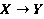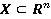В этой статье рассматриваются нейро-нечеткие системы вывода с множеством входов и одним выходом, отображающие , где  и 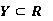 [1]. Система (рис.1) состоит из фуззификатора, базы нечетких правил, нечеткого логического вывода и дефуззификатора.

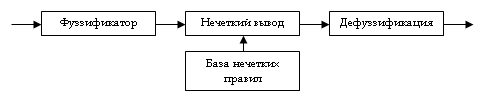
Рис. 1. Нечеткая система вывода

Система управления с нечеткой логикой оперирует нечеткими множествами. Поэтому конкретное значение 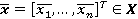входного сигнала модуля нечеткого управления подлежит операции фуззификации, в результате которой ему будет сопоставлено нечеткое множество 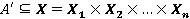. Чаще всего применяется операция фуззификации типа «синглтон»:

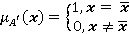   (1)

Нечеткая база правил состоит из набора N нечетких ЕСЛИ-ТО правил вида:

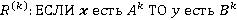,                                                                           (2)

где 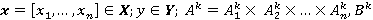 — нечеткие множества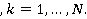

Правило (2) можно представить в виде нечеткой импликации

.

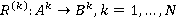Правило 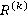 можно интерпретировать как нечеткое отношение, определенное на множестве 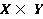, т. е.  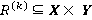— это нечеткое множество с функцией принадлежности

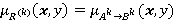.                                                                                          (3)

Нечеткий вывод определяется как отображение нечетких множеств входного пространства 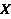на нечеткое множество выходного пространства 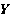. Предположим, что на вход блока выработки решения подано нечеткое множество 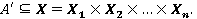Каждое из  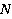правил определяется выходным нечетким множеством 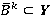, полученным с помощью композиционного правила вывода:

.

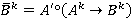Нечеткие множества 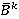, в соответствии с формулой (3) характеризуются функцией принадлежности:

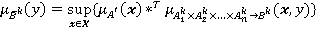                                                         (4)

где 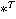 может быть любым оператором из класса Т-норм. Заметим, что при использовании операции фуззификации типа «синглтон»(1), формула (4) принимает вид:

,

где 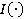 — «инженерная импликация» или нечеткая импликация.

Оператор агрегации, применяемый для того, чтобы получить нечеткое множество 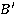 из нечетких множеств  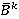— это оператор Т-нормы или Т-конормы в зависимости от типа нечеткой импликации.

Дефуззификатор представляет отображение нечеткого множества 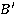 в точку  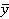из  Существует несколько методов дефуззификации. Например, метод дефуззификации по максимуму функции принадлежности:

.

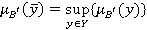Далее рассмотрим общую схему нейро-нечеткой системы вывода [3].

Рис. 2. Структура нейро-нечеткой сети

Она включает оба типа вывода — Мамдани и логический:

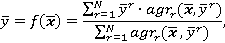
где

     

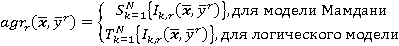
и

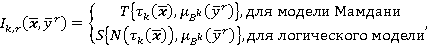
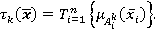
При использовании модели Мамдани и логического типа полученные результаты будут отличаться. В статье предложено использовать гибкую нейро-нечеткую систему типа «И», которая представляет собой следующую комбинацию «инженерной» и нечеткой импликации:

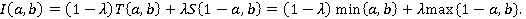
Параметр 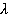 находится в процессе обучения и может принимать значения из интервала [0;1].

Тогда нейро-нечеткая система примет вид:

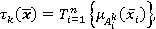
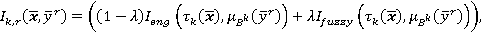
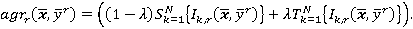
Отметим, что при 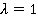 получаем нейро-нечеткую систему Мамдани, а при  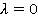— логического типа.

Обучение нейро-нечеткой сети осуществляется с использованием генетического алгоритма [2], который позволяет избежать трудностей, присущих градиентным методам.

Для обеспечения выполнения принципа обобщения используем треугольные нечеткие величины. При данном подходе вид функции принадлежности однозначно определяется тройкой параметров [a, b, c]:

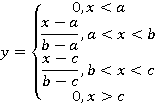
Таким образом, хромосома, кодирующая нейро-нечеткую систему, будет иметь вид:

где a_i, b_i, c_i — параметры функции принадлежности i-ого нечеткого множества, 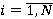;  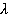— параметр модели вывода.

Для решения поставленной задачи разработана программная схема, структура которой представлена на рис. 3.

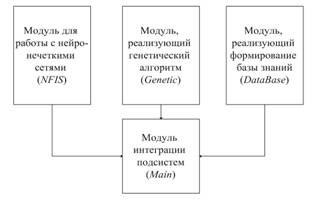
Рис. 3. Функциональная схема программной системы

Модуль для работы с нейро-нечеткими сетями содержит классы, реализующие нечеткие величины, термы, лингвистические переменные, нечеткие правила, а также подпрограммы основных операций с нечеткими величинами, алгоритм нечеткого вывода.

Модуль генетического поиска обеспечивает реализацию генетического алгоритма, кодирование базы правил.

Модуль, реализующий формирование базы знаний, получает на входе обучающие данные и формирует на их основе базу нечетких правил.

Модуль интеграции подсистем реализует основную последовательность действий по выполнению функций системы нечеткого вывода путем вызова соответствующих подпрограмм остальных модулей.

Рассматриваемая нейро-нечеткая система тестировалась на задачах моделирования:

1.                  статической нелинейной функции: рассматривается аппроксимация нелинейной функции, которая описывается выражением

.

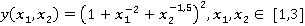Обучающая последовательность состоит из 100 векторов входных данных и соответствующих им значений функции.

2.                  динамического нелинейного объекта: поведение объекта описывается функцией

,

где 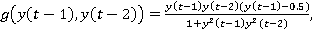 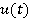 — выходной сигнал.

Обучающая последовательность генерируется для нулевого начального состояния. Для обучения нейро-нечеткой системы используется последовательность состояний объекта для синусоидального входного сигнала вида .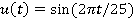

Для оценки полученной нейро-нечеткой системы используется среднеквадратичная ошибка (RSME):

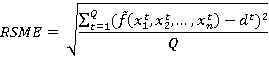
где Q — количество наборов в обучающей выборке; 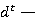значение выходной переменной в t-ом наборе обучающей выборки, 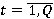;  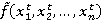— результат нечеткого вывода по -ому набору обучающей выборки.

Результаты эксперимента представлены в таблице 1.

Таблица 1

Результаты тестирования нейро-нечеткой системы

Концепция гибких нейро-нечетких систем позволяет выбрать тип системы (Мамдани или логический) по результатам обучения. Решения тестовых задач свидетельствуют, что гибкая система в результате обучения становится системой Мамдани (параметр

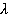 =0) при решении задач аппроксимации. Таким образом, рекомендуется использовать систему типа Мамдани для задач аппроксимации и идентификации.

Литература:

1.     Рутковская, Д. Нейронные сети, генетические алгоритмы и нечеткие системы [Текст] / Д. Рутковский, М. Пилиньский, Л. Рутковский. — М.: «Горячая линия — Телеком», 2004. — 452 с.

2.     Лю, Б. Теория и практика неопределенного программирования [Текст] / Б. Лю. — М.: «БИНОМ. Лаборатория знаний», 2013. — 416 с.

3.     Rutkowski, L. Flexible neuro-fuzzy systems [Текст] / L. Rutkowski. — Boston: Kluwer Academic Publishers, 2004. — 279 c.