В данной работе рассматривается задача о накате одиночной волны на защитные сооружения типа вертикальной стенки с примыкающим к ней затопленным уступом. Решение задачи получено методом преобразования Лапласа и сращивания подобластей.
Ключевые слова: одиночная волна, накат, защитные сооружения.
Идеальная несжимаемая однородная жидкость в состоянии покоя занимает область, ограниченную горизонтальной свободной поверхностью, горизонтальными участками дна с глубинами 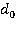 и
и 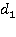 , наклонным участком дна с углом
, наклонным участком дна с углом 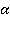 и вертикальной стенкой. Пусть в начальный момент времени
и вертикальной стенкой. Пусть в начальный момент времени 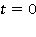 на некотором удалении от вертикальной стенки появляется возмущение в виде одиночной волны, имеющей профиль
на некотором удалении от вертикальной стенки появляется возмущение в виде одиночной волны, имеющей профиль 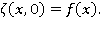 Известно [1], что эта задача — нелинейна. Требуется определить форму свободной поверхности
Известно [1], что эта задача — нелинейна. Требуется определить форму свободной поверхности 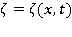 в произвольный момент времени
в произвольный момент времени 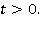 В линейной постановке эта задача сводится к смешанной задаче для волнового уравнения с переменными коэффициентами [1].
В линейной постановке эта задача сводится к смешанной задаче для волнового уравнения с переменными коэффициентами [1].
1. Постановка задачи. Требуется отыскать функцию 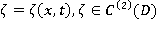 в области
в области
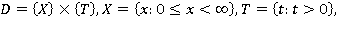
являющуюся решением уравнения
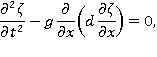
где 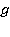 — ускорение свободного падения;
— ускорение свободного падения; 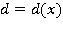 — глубина жидкости
— глубина жидкости
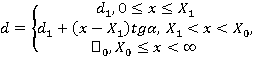
удовлетворяющую начальным условиям
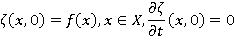
и граничным условиям
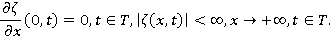
2. Метод решения.
Для построения решения воспользуемся методом сращивания подобластей. Для этого разобьем область 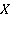 на 3 подобласти точками
на 3 подобласти точками 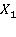 и
и 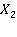 . В каждой из подобластей будем строить решение задачи, определяя неизвестные константы из условий непрерывности волнового профиля и непрерывного изменения скорости в точках сопряжения:
. В каждой из подобластей будем строить решение задачи, определяя неизвестные константы из условий непрерывности волнового профиля и непрерывного изменения скорости в точках сопряжения:
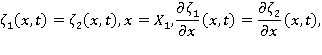
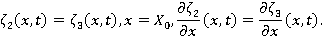
3. Построение решения в подобласти 1.
В подобласти 1 имеем следующую задачу:
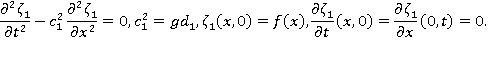
Применим к поставленной задаче преобразование Лапласа. Обозначим изображение функции 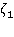 через
через 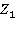 , т. е.
, т. е. 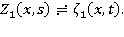 Здесь
Здесь 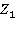 — изображение функции
— изображение функции 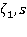 — комплексный параметр. Смешанная задача, с учетом начальных и краевых условий, в пространстве изображений примет вид:
— комплексный параметр. Смешанная задача, с учетом начальных и краевых условий, в пространстве изображений примет вид:
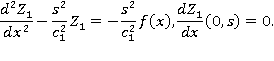
Решая полученную задачу, имеем представление решения в подобласти 1:
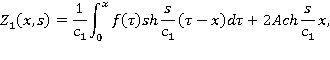
где  — некоторая неизвестная пока константа.
— некоторая неизвестная пока константа.
4. Построение решения в подобласти 2.
Задача в этой подобласти имеет вид:
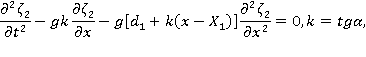
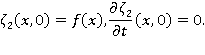
Применим преобразование Лапласа к сформулированной задаче. Обозначим изображение функции 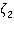 через
через 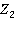 , т. е.
, т. е. 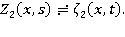 Здесь
Здесь 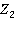 — изображение функции
— изображение функции 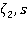 — комплексный параметр. Получим в изображениях следующее уравнение:
— комплексный параметр. Получим в изображениях следующее уравнение:
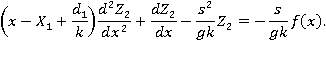
Решением его является выражение:
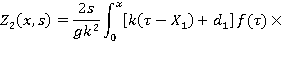
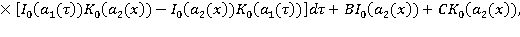
где
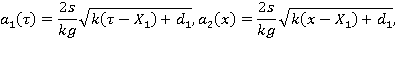
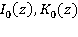 — цилиндрические функции мнимого аргумента,
— цилиндрические функции мнимого аргумента, 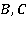 — неизвестные постоянные.
— неизвестные постоянные.
5. Построение решения в подобласти 3.
Задача в этой подобласти имеет вид:
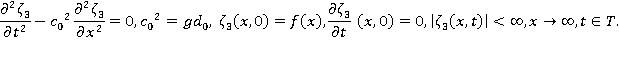
Применим преобразование Лапласа к поставленной задаче. Положим 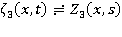 , где
, где 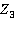 — изображение функции
— изображение функции 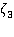 ,
,  — комплексный параметр. Получим в пространстве изображений следующую задачу:
— комплексный параметр. Получим в пространстве изображений следующую задачу:
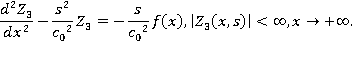
Рассмотрим соответствующее однородное уравнение:
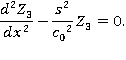
Оно имеет общее решение:
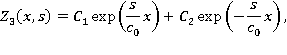
где 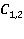 — произвольные константы. Общее решение неоднородного уравнения найдем методом Лагранжа. Представим его в виде:
— произвольные константы. Общее решение неоднородного уравнения найдем методом Лагранжа. Представим его в виде:
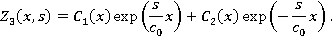
Составим систему уравнений для определения производных неизвестных функций 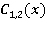 :
:
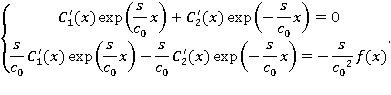
Решая ее, получаем: 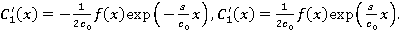 Отсюда, имеем:
Отсюда, имеем:
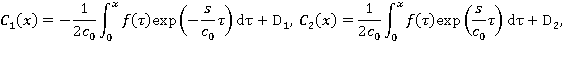
где 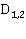 — постоянные. Поэтому
— постоянные. Поэтому
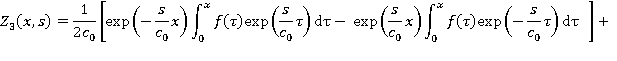
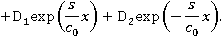
В силу условия ограниченности: 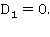 Таким образом, решение задачи в подобласти 3 в пространстве изображений имеет вид:
Таким образом, решение задачи в подобласти 3 в пространстве изображений имеет вид:
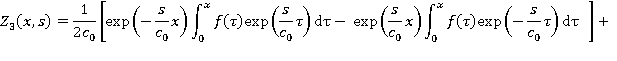
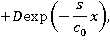
где 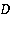 — некоторая постоянная. Перепишем это решение несколько иначе:
— некоторая постоянная. Перепишем это решение несколько иначе:
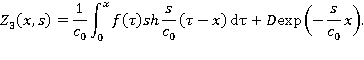
6. Сращивание решений.
Введем обозначения:
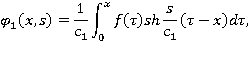
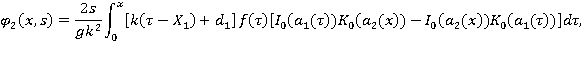
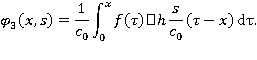
Тогда:
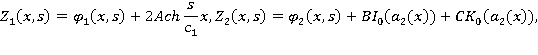
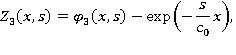
Условия сращивания имеют вид:
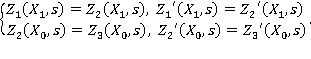
Учитывая предложенные представления решений в подобластях и соотношения между бесселевыми функциями [2]:
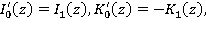
получаем систему уравнений для нахождения неизвестных 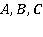 и
и 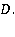 Выпишем ее в матричной форме:
Выпишем ее в матричной форме:
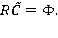
Здесь
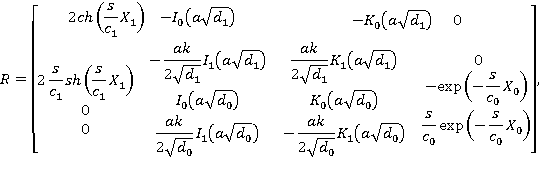
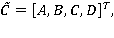
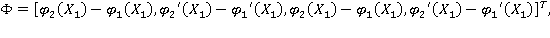
где верхний индекс T означает операцию транспонирования.
Решая эту систему методом исключения, получаем следующие выражения для определения постоянных:
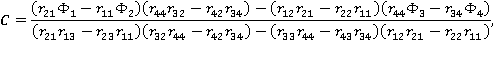
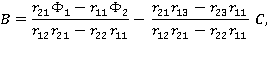
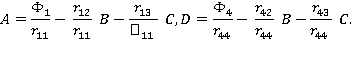
Полученные выражения полностью решают задачу в пространстве изображений. Поскольку они имеют довольно сложный вид, обращение преобразования Лапласа для нахождения решения исходной задачи следует выполнять каким-либо численным методом, например, разложением решения в ряд Фурье [3]. Можно воспользоваться процедурами обращения, содержащимися в математических комплексах Maple или Mathematica [4].
Литература:
1. Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика. Ч.1. — М.: Физматгиз, 1963.
2. Градштейн И. С., Рыжик И. М. Таблицы интегралов, рядов и произведений. —Под ред. А. Джеффри, Д. Цвилингера. — 7-е изд.: Пер. с англ. под ред. В. В. Максимова. — СПб.: БХВ-Петербург, 2011.
3. Крылов В. И., Скобля Н. С. Методы приближенного преобразования Фурье и обратного преобразования Лапласа. — М.: Наука, 1974.
4. Кристалинский В. Р., Кристалинский Р. Е. Преобразования Фурье и Лапласа в системах компьютерной математики: Учебное пособие для вузов. — М.: Горячая линия-Телеком, 2006.







