Статья описывает актуальность использования параллельных технологий на основе графических процессоров. Рассмотрена задача гравитационного взаимодействия N-тел. Для анализа ускорения использованы различные графические процессоры.
Ключевые слова:CUDA, гравитационное взаимодействие, ускорение, Tesla C1061.
Целью данной работы являлась реализация задачи N-тел прямым методом (PP — «частица-частица»), где учитывается гравитационное взаимодействие всех частиц друг с другом, на основе вычислительного кода и последующее применение параллельной технологии CUDA для ускорения выполнения расчетной части кода.
Актуальность данной работы обусловлена тем, что современные численные модели становятся всё более затратными с точки зрения вычислительных возможностей. В связи с этим параллельные технологии приобретают всё большую распространенность. Особый интерес на сегодняшний день представляют вычисления на графических процессорах.
Прямой метод расчета взаимодействия всех частиц представляется наиболее простым и понятным для реализации и обеспечивает наилучшую точность вычисления гравитационной силы. Но в то же время он требует наибольших машинных ресурсов, поскольку каждая частица взаимодействует с каждой. Исходя из этих особенностей, данный метод можно использовать для создания тестовой модели для проверки наиболее важных принципиальных результатов [1]. Главным преимуществом этой модели будет возможность определять значения нужных параметров с такой же точностью, что и арифметическая точность ЭВМ.
Численная модель была построена на основе закона тяготения Ньютона, в случае аддитивности сил гравитации, который описывает попарное взаимодействие всех точек системы. При этом задается некоторое начальное распределение векторов скоростей и радиус-векторов. Для программной реализации данной модели использовалась численная схема Эйлера второго порядка точности по времени. Полученная численная схема описывается следующей системой уравнений:
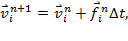
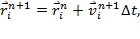
где v — скорость движения частицы,
r — радиус частицы,
f — гравитационная сила,
∆t — шаг по времени.
На основе численной схемы была реализована компьютерная модель, описывающая соответственное гравитационное взаимодействие. Для дальнейшего тестирования были написаны два алгоритма: последовательный и параллельный.
Для построения параллельной схемы использовалась технология распараллеливания на графических процессорах. CUDA представляет собой неграфические вычисления на графических процессорах. Используя особенности архитектуры GPU, она позволяет в разы, в десятки раз, ускорять программы, выполняемые на CPU. Ядра CPU созданы для исполнения одного потока последовательных инструкций с максимальной производительностью, в то время как GPU проектируются для быстрого исполнения большого числа параллельно выполняемых потоков инструкций.
Модель программирования CUDA предполагает группирование потоков. Потоки объединяются в блоки потоков — одномерные или двумерные сетки потоков, взаимодействующих между собой при помощи разделяемой памяти и точек синхронизации.
Для проверки релевантности результатов, получаемых в ходе работы программы, использовалось точное аналитическое решение задачи двух тел. Для ситуации, когда два тела равной массы, в начальный момент времени имеют вектора скоростей, ортогональные линии, соединяющей их, и направлены в противоположные стороны, траектория движения тел будет представлять собой две концентрические окружности (или эллипсоиды). Подобную ситуацию можно увидеть на рисунке 1, отображающем результат работы тестовой программы. Последовательная и параллельная программа показали полностью идентичные результаты.
Так как программа в дальнейшем будет использована в научных расчетах гравитационного взаимодействия бесстолкновительных звездных систем, представляющих собой галактические диски, в каждой из программ начальные условия загружаются из внешнего файла данных, заранее сформированного специальным программным комплексом, отвечающим за корректное начальное распределение тел системы.
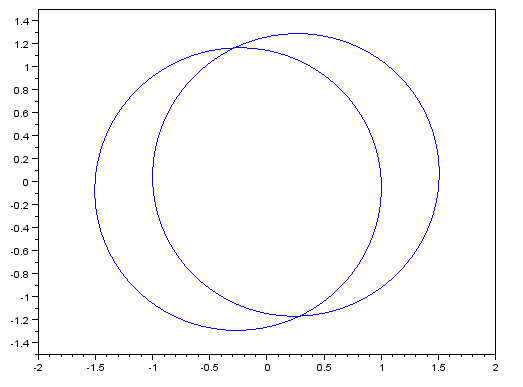
Рис. 1. Гравитационная задача двух тел
Для тестирования получаемого ускорения на графическом процессоре использовались GPU различного класса, а именно:
- GeForce 9400 GT (офисная видеокарта для ПК);
- GeForce GT 555M (мощная видеокарта для ноутбуков);
- Tesla C1061 (видеокарта, предназначенная для специализированных неграфических вычислений).
Производительность вычислений на этих устройствах сравнивалась с расчетными мощностями центрального процессора Intel Core i5 на одном ядре. Для тестирования производились расчеты на нескольких вариантах начальных данных, отличающихся количеством гравитирующих тел. Результаты, представленные в виде времени (миллисекунды) выполнения одной итерации внешнего цикла, показаны в таблице 1.
Таблица 1
Время выполнения расчетов
|
Кол-во частиц |
Intel Core i5 |
GT 9400 |
GT 555M |
Tesla C1061 |
|
1024 |
26 |
18,00 |
0,90 |
2,63 |
|
4*1024 |
425 |
183,00 |
6,00 |
11,00 |
|
8*1024 |
1750 |
681,00 |
22,0 |
25,00 |
|
10*1024 |
2843 |
1043,00 |
38,00 |
32,00 |
Из полученных данных видно, что достигается ускорение в несколько десятков раз. Для более наглядного отображения информации представлен рисунок 2, показывающий результирующее ускорение работы программы на GPU в сравнении с CPU.
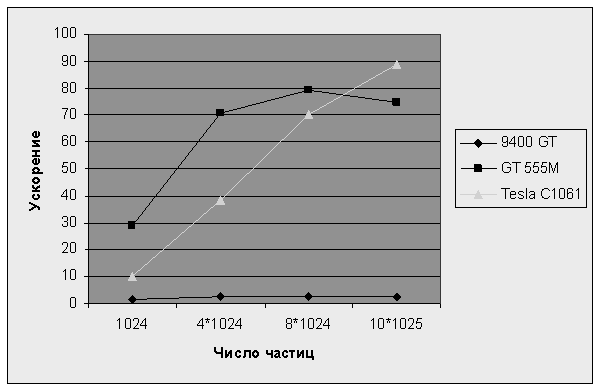
Рис. 2. Полученное ускорение
Из данного графика видно, что пиковое ускорение примерно в 80 раз на карте GT 555M достигается при 8192 частицах. В то время как максимум производительности картой Tesla C1061 для построенного алгоритма не был достигнут.
В процессе тестирования были получены результаты, показывающие многократное ускорение выполнения программы, решающей гравитационную задачу N-тел, при использовании параллельных технологий, основанных на вычислительных особенностях графических процессоров. Это показывает, что данная технология достаточно актуальна на сегодняшний день и позволяет получать значительный прирост производительности.
Литература:
1. Морозов А. Г., Хоперсков А. В. Физика дисков. — Волгоград, 2005.
2. Jason Sanders, Edward Kandrot CUDA by Example An Introduction to General-Purpose GPU Programming — 2010.







