В статье изложен способ повышения эффективности проектирования распределенной вычислительной сети. Разработаны математическая модель и программный комплекс оптимального выбора распределенной вычислительной сети.
Результаты математического моделирования и формализации модели на ПЭВМ позволяют снизить финансовые и временные издержки, повысить обоснованность принимаемого решения и сократить срок окупаемости.
Ключевые слова: Математическая модель, метод экспертных оценок, симплекс-метод, оптимальное решение, архитектура программного комплекса, трехуровневая модель.
В настоящее время наблюдается широкое распространение распределенных вычислительных сетей. Это объясняется их преимуществами, основанными на совместном использовании информации и быстром доступе к данным. Распределенные вычислительные сети решают задачи в интересах корпорации, ее отделений и предприятий [1, c.429].
Выбор эффективного варианта распределенной вычислительной сети является актуальной задачей. Для решения поставленной задачи разработана математическая модель выбора оптимального варианта распределенной вычислительной сети, формализованная на ПЭВМ.
Постановка задачи оптимизации распределенной вычислительной сети формулируется следующим образом: из числа альтернативных вариантов распределенной вычислительной сети необходимо выбрать наилучший вариант, максимизирующий чистый приведенный эффект и удовлетворяющий финансовым ограничениям.
Математическая модель оптимизации включает в себя два этапа:
1. Методом экспертных оценок формируются альтернативные варианты распределенной вычислительной сети.
2. Методом математического программирования определяется оптимальный вариант из числа альтернативных, выбранных на первом этапе.
Математическая модель линейного программирования имеет вид:
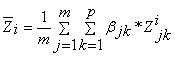
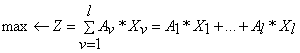
при ограничениях
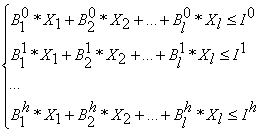
где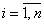 
количество групп экспертов;
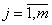— число экспертов в группе, оценивающих варианты проектов;
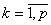— количество оборудования, выбираемых экспертом;
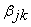— вес, выбранный j-м экспертов для k-ого оборудования;
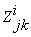— оценка, данная j-м экспертом i-ой группы для k-ого оборудования;
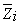— средняя оценка проекта i-ой группы;
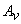— чистый приведенный эффект v-ого проекта;
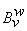— инвестиционные затраты v-ого проекта в w-ом периоде времени;
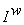— средства финансирования в w-ом периоде времени;
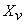— доля финансирования v-ого проекта;
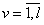— номер инвестиционного проекта;
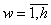— номер периода времени [2, с. 165].
Оптимальное решение определяется методом Гаусса-Жордана.
Алгоритм метода Гаусса-Жордана включает этапы:
1 Этап. Определение начального допустимого решения.
2 Этап. Проверка на оптимальность. Если решение оптимально переход на 5 этап.
3 Этап. Выбор включаемой и исключаемой переменных.
4 Этап. Определение нового плана. Переход на 2 этап.
5 Этап. Печать оптимального решения [3, c. 110].
Математическая модель формализована на ПЭВМ. Разработанный программный комплекс предоставляет автоматизированный выбор наилучшего варианта проекта распределенной вычислительной сети.
В основе архитектуры программного комплекса используется трехуровневая модель приложения. Трехуровневая модель включает три уровня: представление, бизнес — логика, данные.
Уровень представления — интерфейс обеспечивающий взаимодействие пользователя с приложением.
Уровень бизнес — логики — правило обработки данных.
Уровень данных — взаимодействие с базой данных.
Программный комплекс включает функции:
1. Ввод исходных данных.
2. Реализация метода экспертных оценок.
3. Определение оптимального варианта распределенной вычислительной сети.
4. Поиск по базе данных.
5. Добавление в базу данных.
6. Редактирование характеристик оборудования.
7. Просмотр сетевого оборудования.
8. Вывод списка сетевого оборудования.
Программный комплекс реализован на языке Qt Creator C++.
После запуска программы, появляется заставка (рис.1).
Рис.1. Заставка программного комплекса
Вводятся исходные данные в соответствии с техническим заданием (рис.2 — рис.4).
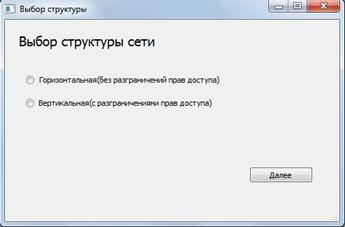
Рис. 2. Выбор структуры сети
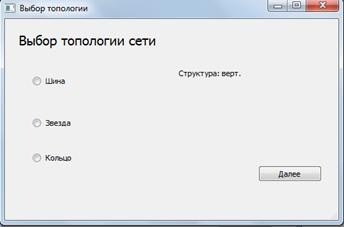
Рис. 3. Выбор топологии
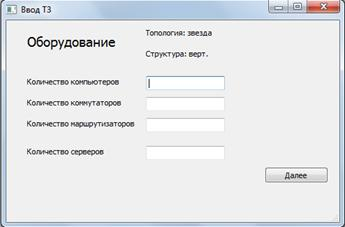
Рис. 4. Ввод данных по рабочим станциям и сетевому оборудованию
После ввода данных реализуется первый этап — формирование альтернативных проектов с использованием метода экспертных оценок (рис.5 — рис.6).
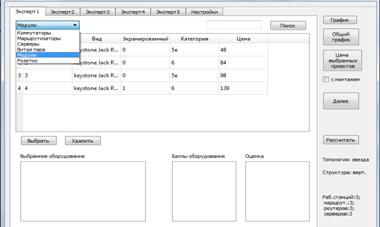
Рис. 5. Первый эксперт первой группы. Выбор оборудования
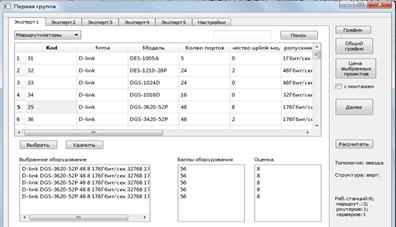
Рис. 6. Результат выбора первого эксперта первой группы
Количество групп и число экспертов в группах можно изменять в программном комплексе.
Результат работы экспертов представляется в графическом виде (рис.7 — рис.8)
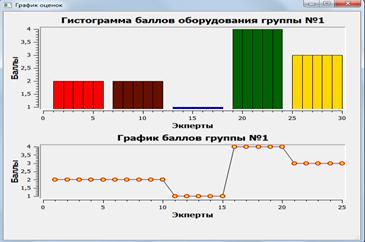
Рис. 7. Результат работы экспертов первой группы
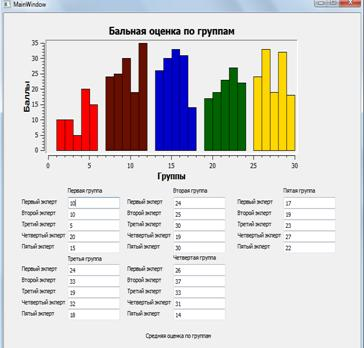
Рис. 8. Результаты работы групп экспертов
Суммарные затраты на реализацию проектов приведены на рис.9.
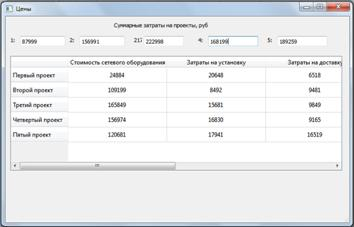
Рис. 9. Сумарные затраты на реализацию проектов
Реализуется второй этап математической модели — выбор оптимального варианта проекта распределенной вычислительной сети из числа альтернативных вариантов первого этапа (рис.10)
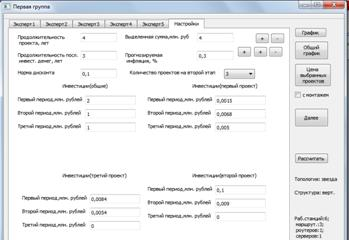
Рис. 10. Ввод данных для реализации второго этапа математической модели
Нажимаем кнопку <Рассчитать>. Получаем оптимальное решение (рис. 11).
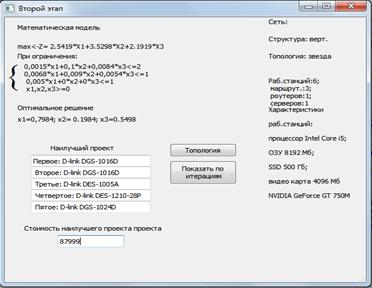
Рис. 11. Оптимальноео решение
Программный комплекс позволяет посмотреть определение оптимального решения по итерациям и вывести графическое представление топологии сети.
Результаты проведенных исследований позволили сделать выводы.
1. Разработана математическая модель выбора оптимального варианта проекта распределенной вычислительной сети.
2. Разработан программный комплекс выбора оптимального проекта распределенной вычислительной сети.
3. Разработанная математическая модель, формализованная на ПЭВМ, позволяет снизить финансовые и временные издержки, повысить качество и обоснованность принимаемого решения в проектировании распределенной вычислительной сети и сократить срок окупаемости.
4. Результаты работы могут быть использованы для дальнейшего исследования.
Литература:
1. Пятибратов А. П. Вычислительные системы, сети и телекоммуникации: Учебник. — 2-е изд, перераб. и доп./А. П. Пятибратов, Л. П. Гудыно, А. А. Кириченко; Под ред. А. П. Пятибратова. — М.: Финансы и статистика, 20025. — 512 c.
2. Семахин А. М. Математическая модель оптимизации информационной системы. Вестник Курганского государственного университета. — Серия «Технические науки». — Вып. 5. — Курган: Изд-во Курганского гос. ун-та, 2010. — 220 с.
3. Таха Хемди. Введение в исследование операций, 7 — издание.; Пер. с англ. — М.: Издательский дом “Вильямс”, 2005. — 912 с.
