В настоящее время появилась возможность решения математических задач без составления компьютерных программ на алгоритмических языках. Причиной этого является разработка специальных математических программ — математических систем. В вузах и научных учреждениях чаще всего применяются математические системы: MATHCAD, MATLAB, Maple, Mathematika. С применением математических систем учебный процесс становится интереснее, студенты понимают содержание занятия быстрее, глубже, а для укрепления преподаваемых понятий и решения задач остаётся больше времени.
В последнее время задачи вычислительной математики [1,2] по преимуществу решают в математической системе MATHCAD [3–6]. Именно в MATHCAD задача формулируется в наиболее естественном математическом виде, а в других математических системах шаги алгоритма решения задачи записываются с помощью команд системы.
В статье алгоритмы методов конечно-разностных схем приближённого решения линейного параболического и гиперболического дифференциальных уравнений с краевыми условиями организованы в математической системе MATHCAD.
1. Метод решения дифференциальных уравнений в MATHCAD.
Пусть дана краевая задача для дифференциального уравнения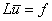 в непрерывной области D. Сопоставим ей некоторую дискретную задачу
в непрерывной области D. Сопоставим ей некоторую дискретную задачу 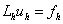 в дискретной области
в дискретной области 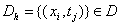 , где
, где 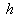 - параметр дискретизации и
- параметр дискретизации и 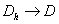 , при
, при 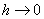 , и
, и 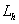 - дискретный оператор, а переменные
- дискретный оператор, а переменные 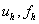 - дискретные функции, такие, что
- дискретные функции, такие, что 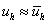 ,
, 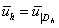 ,
, 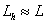 ,
, 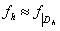 , т. е.
, т. е. 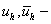 каркас –таблица значений функций
каркас –таблица значений функций 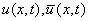 на сетке точек
на сетке точек 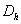 . В качестве дискретной задачи мы берем конечно-разностную схему (КРС), и тогда дискретная задача есть система алгебраических уравнений (СЛАУ), и элементы
. В качестве дискретной задачи мы берем конечно-разностную схему (КРС), и тогда дискретная задача есть система алгебраических уравнений (СЛАУ), и элементы 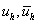 есть таблица значений функций. В MATHCAD идея решения дискретной задачи
есть таблица значений функций. В MATHCAD идея решения дискретной задачи 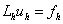 очень проста и естественна:
очень проста и естественна: 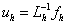 . Эта идея имеет место даже тогда, когда элементы
. Эта идея имеет место даже тогда, когда элементы 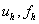 являются матрицами:
являются матрицами: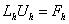 , где
, где 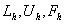 — матрицы [3–6].
— матрицы [3–6].
Команды в MATHCAD отличаются от математических формул с лишь следующим: знак (:=) означает определение, знак равенство (=) или стрелка (→) означает вывод вычисленного значения. После знака «записывается текст замечание.
2. Дифференциальные краевые задачи и КРС [1,2].
А) Рассмотрим краевую задачу для параболического уравнения:
,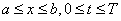 ,(1)
,(1)
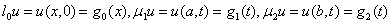 . (2)
. (2)
(1), (2) называется краевой задачей для параболического дифференциального уравнения (КЗ для ПДУ). Функция 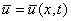 , удовлетворяющая ПДУ и краевым условиям называется точным решением:
, удовлетворяющая ПДУ и краевым условиям называется точным решением: 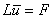 ,
, 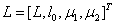 ,
, 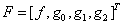 .
.
Явная КРС 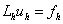 ,для ПДУ с точностью
,для ПДУ с точностью 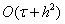 имеет вид:
имеет вид:
(3)
Неявная КРС 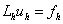 ,для ПДУ с точностью
,для ПДУ с точностью 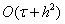 имеет вид:
имеет вид:
(4)
К (3) и (4) необходимо присоединить начальные и краевые условия
,(5)
Явная КРС для ПДУ решается с помощью реккурентных формул:
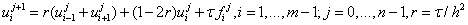 , (6)
, (6)
Неявная КРС для ПДУ на каждом слое j сводиться к системе линейных уравнений:
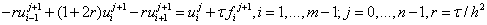 . (7)
. (7)
Неявная КРС для ПДУ на каждом слое j есть система линейных уравнений с трёхдиагональной матрицей и, начиная с первого слоя, решается методом прогонки.
Вводя матрицу 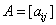 с коэффициентами
с коэффициентами 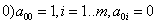 ;
;
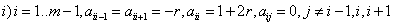 ;
; 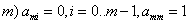 ,
,
и векторы 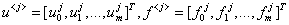 неявную схему можно записать в векторно-матричном виде, связывающим неизвестные
неявную схему можно записать в векторно-матричном виде, связывающим неизвестные 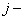 го и
го и 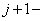 го слоёв
го слоёв
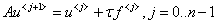 . (8)
. (8)
В) Рассмотрим краевую задачу для гиперболического уравнения:
, 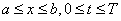 ,(9)
,(9)
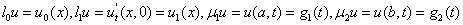 . (10)
. (10)
(9), (10) называется краевой задачей для гиперболического дифференциального уравнения (КЗ для ГДУ). Функция 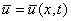 , удовлетворяющая ГДУ и краевым условиям называется точным решением:
, удовлетворяющая ГДУ и краевым условиям называется точным решением: 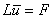 ,
, 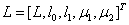 ,
, 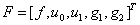 .
.
Явная КРС 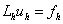 ,для ГДУ с точностью
,для ГДУ с точностью 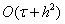 имеет вид:
имеет вид:
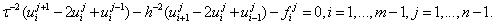 ,
,
Неявная КРС 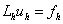 ,для ГДУ с точностью
,для ГДУ с точностью 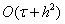 имеет вид:
имеет вид:
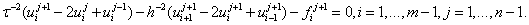 ,
,
Используя матрицу 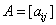 , неявную схему можно записать в векторно-матричном виде,
, неявную схему можно записать в векторно-матричном виде,
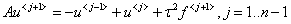 , (11)
, (11)
которая связывает неизвестные 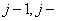 го и
го и 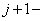 го слоёв.
го слоёв.
Явная КРС для ГДУ решается с помощью рекуррентных формул: ,
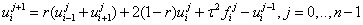 .
.
Неявная КРС для ГДУ на каждом слое j есть система линейных уравнений с трёхдиагональной матрицей и, начиная со второго слоя, решается методом прогонки:
,
Для ГДУ в явной и неявной КРС аппроксимацию можно улучшить до 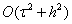 , если аппроксимацию начальных условий взять в следующем виде:
, если аппроксимацию начальных условий взять в следующем виде:
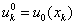 ,
,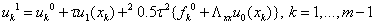 .
.
3. Организация решения КРС для ПДУ в MathCAD.
Пусть дана краевая задача для параболического уравнения (1),(2) с данными:
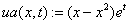 ,
,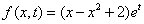 . (12)
. (12)
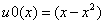 ,
, 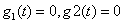 . (13)
. (13)
A) Решение с помощью внутренней функции Pdesolve.
Вводим в окне MathCAD следующие команды:
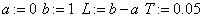 «область
«область
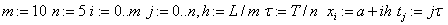 «сетка
«сетка
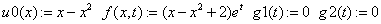 «начальные данные
«начальные данные
Given 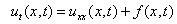 «ПДУ, равенство жирное
«ПДУ, равенство жирное
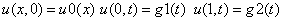 «краевые условия, равенство жирное
«краевые условия, равенство жирное
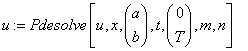
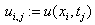 «обращение к Pdesolve
«обращение к Pdesolve
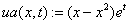
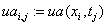 «решения
«решения 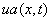 ,
,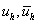
«выведем таблицу значений приближённого решения
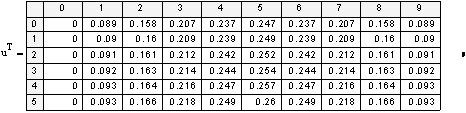
«выведем таблицу значений точного решения
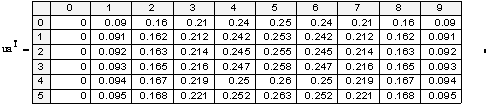
«выведем графики приближённого и точного решений
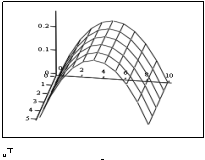
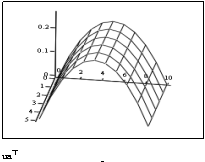
B) Решение явной КРС для ПДУ в MathCAD.
Записываем в окне MathCAD следующие команды:
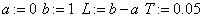 «область
«область
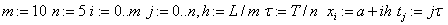 «сетка
«сетка
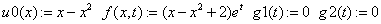 «начальные данные
«начальные данные
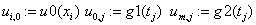 «дополнительные условия
«дополнительные условия
«послойное вычисление и вывод 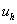
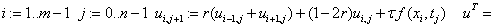
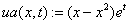
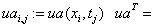 «вычисление и вывод
«вычисление и вывод 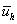
Отметим, что таблицы значений приближённого и точного решений совпадают с соответствующими таблицами из пункта А), полученными внутренней функцией Pdesolve.
C) Решение неявной КРС для ПДУ в MathCAD.
Записываем в окне MathCAD следующие команды:
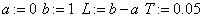 «область
«область
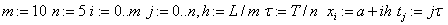 «сетка
«сетка
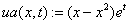
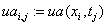 «точное решение и его каркас
«точное решение и его каркас 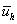
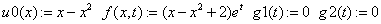 «начальные данные
«начальные данные
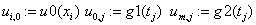 «дополнительные условия
«дополнительные условия
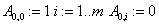
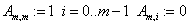 «ввод матрицу СЛАУ
«ввод матрицу СЛАУ
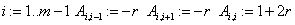 «ввод матрицу СЛАУ
«ввод матрицу СЛАУ
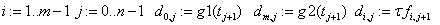
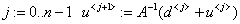 «вычисление
«вычисление 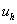
A= «выведем для контроля матрицу А
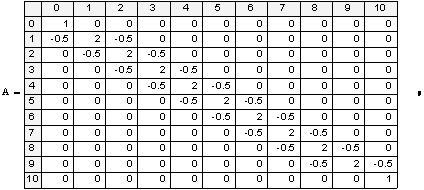
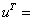 «вывод каркаса решения
«вывод каркаса решения 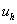
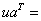 «вывод каркаса решения
«вывод каркаса решения 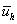
Отметим, что таблицы значений приближённого и точного решений совпадают с соответствующими таблицами из пункта А), полученными внутренней функцией Pdesolve.
4. Организация решения КРС для ГДУ в MathCAD.
Рассмотрим краевую задачу для гиперболического уравнения (9),(10) с данными:
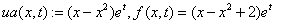 , (12)
, (12)
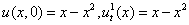 ,
, 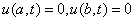 . (14)
. (14)
A) Решение с помощью внутренней функции Pdesolve.
Для решения ГДУ внутренней функцией записываем следующие команды:
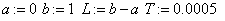 «область
«область
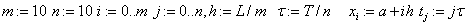 «сетка
«сетка
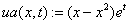
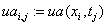 «точное решение и его каркас
«точное решение и его каркас 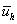
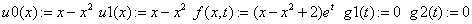 «данные
«данные
Given 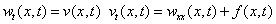 «ГДУ, равенство жирное
«ГДУ, равенство жирное
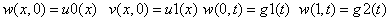 «данные,
«данные,
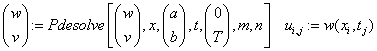 «обращение к Pdesolve
«обращение к Pdesolve
«Выведем таблицу точного и приближённого решений
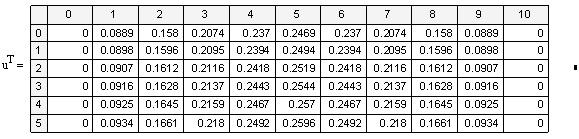
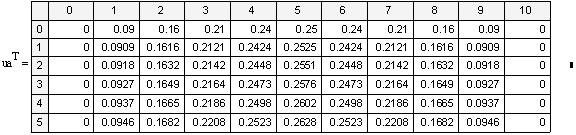
В) Решение явной КРС для ГДУ в MathCAD.
Записываем следующие команды (шаги алгоритма):
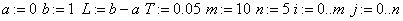 «область
«область
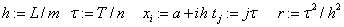 «сетка
«сетка
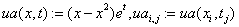 «точное решение и его каркас
«точное решение и его каркас
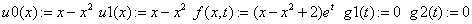 «данные
«данные
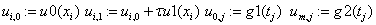 «явная КРС
«явная КРС
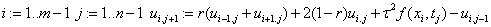
«Вывод таблицу значений приближённого и точного решений:
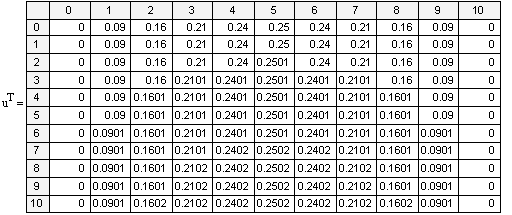

«Только при увеличении десятичных разрядов можно увидеть разницу.
С) Решение неявной КРС для ГДУ в MathCAD.
Записываем следующие команды (шаги алгоритма):
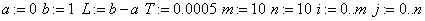 «область
«область
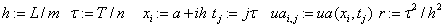 «сетка
«сетка
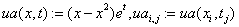 «точное решение и его каркас
«точное решение и его каркас
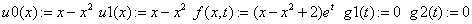 «данные
«данные
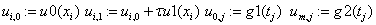 «дополнительные условия
«дополнительные условия
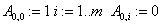 «задание матрицы неявной КРС
«задание матрицы неявной КРС
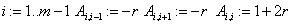 «задание матрицы неявной КРС
«задание матрицы неявной КРС
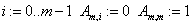 «задание матрицы неявной КРС
«задание матрицы неявной КРС
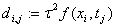 «задание правой части в КРС
«задание правой части в КРС
«Организуем вычисления по неявной схеме
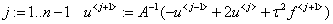
«Для контроля выведем значения приближённого решения на 0-ом, и 1-ом слоях
 ,
,

«Выведем таблицу значений точного и приближённого решений
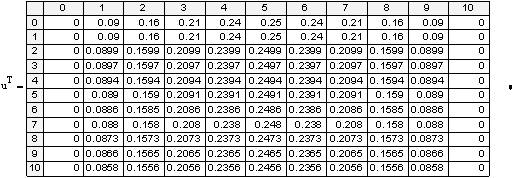
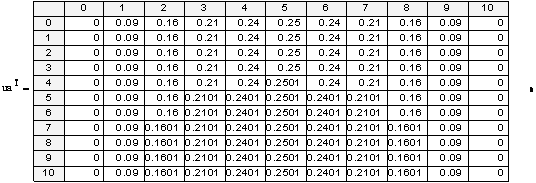
«Выведем графики приближённого и точного решений:
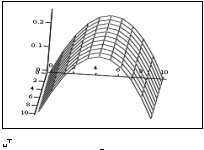
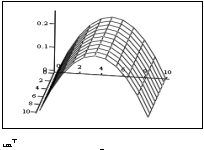
Литература:
1. Марчук Г. И. Методы вычислительной математики. М.: Наука, 1981.-456 c.
2. Вержбицкий В. М. Основы численных методов. М.:ВШ, 2002.-840 с.
3. Поршнев С. В., Беленкова И. В. Численные методы на базе MATHCAD.СПб, 2005.-464 с.
4. Ракитин В. И. Руководство по ВМ и приложения MATHCAD.М.:ФМ, 2005.-264 с.
5. Имомов А. Организация численных методов в MATHCAD. Молодой учёный, № 6(65), май 1, 2014 г.-с. 15–19.
6. Ирискулов С. С., Исманова К. Д., Олимов М., Имомов А. Численные методы и алгоритмы. MATHCAD. Учебное пособие. -Наманган, Изд-во «Наманган», 2013.-278с.







