Ключевые слова: математические методы, эконометрика, множественная регрессия.
Эконометрические модели, могут быть применены в любой сфере нашей жизни, по математическим моделям, можно выявить зависимость многих факторов друг от друга.
В данной статье автор рассматривает зависимость оценки на экзамене от работы студента, а так же определяется степень объективности преподавателей во время выставления оценки.
В моделях множественной регрессии зависимая переменная является функцией многих факторов. В нашей задаче нам требуется выявить зависимость оценки на экзамене от нескольких факторов, а именно: оценки за лабораторную работу, от активности на семинаре, от посещаемости лекций.
Данные для работы были взяты с официального сайта Саратовского государственного университета из электронного журнала для студентов. Статистика была взята по двум группам 2 курса по дисциплине «Математический анализ».
Таблица 1
Данные об успеваемости студентов
|
Y (оценка на экзамене) |
Посещаемость лекций в % (P) |
Ответы на семинарах в течение семестра (O) |
Баллы за лабораторную работу (L) |
|
49 |
65 |
1 |
1 |
|
50 |
60 |
1 |
1 |
|
50 |
63 |
1 |
10 |
|
50 |
68 |
1 |
12 |
|
51 |
55 |
1 |
15 |
|
51 |
56 |
1 |
10 |
|
51 |
76 |
1 |
15 |
|
56 |
74 |
1 |
12 |
|
57 |
69 |
2 |
14 |
|
59 |
68 |
2 |
16 |
|
… |
…. |
…. |
…. |
|
92 |
86 |
7 |
20 |
|
93 |
87 |
6 |
19 |
|
94 |
78 |
7 |
20 |
|
96 |
79 |
6 |
20 |
|
96 |
78 |
7 |
20 |
|
96 |
76 |
7 |
20 |
|
96 |
75 |
7 |
20 |
|
96 |
79 |
7 |
20 |
Первым этапом работы является составление корреляционной матрицы для выявления зависимости между факторами.
Для этого мы используем сервис «Анализ данных»-«Корреляция»
Таблица 2
Матрица Корреляции
|
Y (оценка на экзамене) |
Посещаемость лекций в % (P) |
Ответы на семинарах в течение семестра (O) |
Баллы за лабораторную работу (L) |
|
|
Y (оценка на экзамене) |
1 |
|||
|
Посещаемость лекций в % (P) |
0,658420652 |
1 |
||
|
Ответы на семинарах в течение семестра (O) |
0,971339338 |
0,626633604 |
1 |
|
|
Баллы за лабораторную работу (L) |
0,633590896 |
0,446278343 |
0,628818 |
1 |
Таким образом мы видим, что между факторными переменными (ответы на семинарах, баллы за лабораторную работу, посещаемость лекций) и результативной переменной существует прямая зависимость.
Однако изучив таблицу корреляции, мы можем сделать вывод о том, что наибольшее влияние на оценку студента на экзамене оказывает именно работа на семинарах. По статическим данным, процентное соотношение посещений лекций у всех студентов примерно одинаковое, баллы за лабораторную работу также имеют небольшое отклонение. Соответственно ключевым фактором являются ответы на семинарских занятиях, что подтверждают наши расчеты корреляции.
Также в таблице корреляции, мы видим высокую зависимость между факторными переменными. С первого взгляда это можно принять за мультиколлинеарность. Однако это не так, ведь добросовестный студент будет ходить на лекции, чтобы хорошо отвечать материал на семинарах, а на семинарах задавать вопросы по лабораторной работе. Таким образом, мы делаем вывод, что на самом деле взаимосвязь между факторными переменными логична и объективна.
Следующий шаг нашей работы – построение модели для Y^.
Тип нашей модели – аддитивный.
А значит наша модель будет иметь вид Y^= a+b1*X1+b2*X2+b3*x3.
С помощью метода наименьших квадратов и сервиса «Поиск решения» находим коэффициенты а, b1, b2, b3
Для этого сначала мы вводим произвольные a, b1, b2, b3.
Затем в сервисе «Поиск решения» целевой функцией мы устанавливаем сумму квадратов остатков =CУММ (Y^-Y)^2 и минимизируем ее. Изменяем переменные a, b1, b2, b3. Соответственно, наша модель принимает следующий вид.
Таблица 3
Оцененная функция Y
|
Ученики |
Y (оценка на экзамене) |
Y^ |
|
1 |
49 |
49,178 |
|
2 |
50 |
38,43168 |
|
3 |
50 |
77,28292 |
|
4 |
50 |
21,41668 |
|
5 |
51 |
22,82278 |
|
6 |
51 |
19,30752 |
|
7 |
51 |
22,82278 |
|
…. |
…… |
…… |
|
45 |
96 |
100 |
|
46 |
96 |
100 |
Построим график Y и Y^ и на основе этого графика оценим нашу модель и ее применимость в реальных условиях.
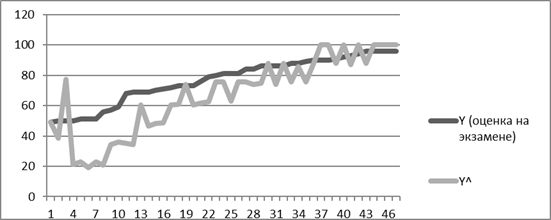
Рис. 1 Зависимость между реальной функцией и оцененной.
В целом мы видим, что модель, официально принятая для оценки работы студента работает в реальной жизни, реальные данные показывают интересную динамику. Чем выше балл студента, тем качественнее использует преподаватель систему оценки. Чем ниже балл студента (между 48 и 70) тем более субъективно преподаватель оценивает работу студента, троечникам преподаватели попросту завышают оценки, давая им шанс исправиться в будущем.
Также мы можем оценить нашу модель с помощью регрессионного анализа. Используем сервис регрессия. Для входного интервала Y выбираем Y^, для входного интервала Х столбики трех факторных переменных.
Результаты регрессионного анализа.
R-квадрат 0, 907653 и коэффициент Фишера 140,8788 говорят о том,0020то в целом мы правильно выстроили модель. Однако стандартная ошибка 7,9 говорит о ее неточности. Однако эта неточность уже была нами объяснена как субъективная оценка преподавателя конкретного студента.
Литература:
1. Орлов А.И., Эконометрика. Учебник. М.: Издательство "Экзамен", 2002.
2. Статистика. Учебник для ВУЗов под редакцией Елисеевой И.И. М.: Проспект 2006. - 443 с.
3. Эконометрика. Учебник для ВУЗов под редакцией Елисеевой И.И. М.: Финансы и статистика 2004.- 344 с.
4. В.Ф. Комиссарчик. Эконометрика: Учебное пособие. Тверь: ТГТУ 2003.- 77 с.







