Статья посвящена одному из разделов теории чисел — диофантовым уравнениям — как средству реализации интеграционных связей математического образования.
Учитель готовится к хорошему уроку всю жизнь… и, чтобы дать ученикам искорку знаний, учителю надо впитать целое море света.
В. А. Сухомлинский.
Одной из целей математического образования, нашедшей отражение в федеральном компоненте государственного стандарта по математике, является интеллектуальное развитие учащихся. Эта цель выходит на одно из ведущих мест при изучении математики на повышенном уровне. Поэтому в современных условиях значительно повышается необходимость создания оптимальной системы интегративного содержания образования и процесса обучения. Интеграция является сегодня одной из определяющих тенденций познавательного процесса.  Одним из средств реализации интеграционных связей математического образования является использование историко-математических сведений в учебном процессе [4, 5]. В частности, решение старинных задач в формулировке первоисточников, изучение истории их решения, сравнение различных методов решения подобных задач позволяет достичь указанные цели.
Одним из средств реализации интеграционных связей математического образования является использование историко-математических сведений в учебном процессе [4, 5]. В частности, решение старинных задач в формулировке первоисточников, изучение истории их решения, сравнение различных методов решения подобных задач позволяет достичь указанные цели.
В связи с вышеизложенным, тема «Диофантовы уравнения», то есть уравнения в целых и рациональных числах, является одной из актуальных в современном отечественном математическом образовании. Особенно важным является то, что в последнее время диофантовы уравнения различного вида стали одним из источников формирования базы задач типа С6 Единого Государственного Экзамена по математике Российской Федерации.
Поскольку одним из основных отличий задачи С-6 от остальных задач ЕГЭ является ее явно выраженный нестандартный характер, а сведения, необходимые для решения этой задачи, могут относиться к самым различным разделам школьного курса, построение решения может потребовать нетривиальных идей и методов, постольку смыслом включения задачи С-6 в состав контрольно-измерительных материалов является именно диагностика уровня интеллектуального развития учащихся. Недаром данная проблематика берет свои истоки с самого зарождения математики.
Проследим, как осуществлялось развитие и происходило становление теории диофантовых уравнений. Если обратиться к истории, то можно заметить, что конкретные задачи такого рода были решены еще в Древнем Вавилоне около 4 тысяч лет тому назад. Древнегреческий математик Диофант, который жил около 2 тысяч лет тому назад, в своей книге «Арифметика» решил большое число таких и более сложных уравнений в целых числах, и описал общие методы их решения.
Комментировать Диофанта начали ещё в древности. Разбору его книг были посвящены труды знаменитой Гипатии, дочери Теона Александрийского. Свое новое «рождение» идеи Диофанта получили в Константинополе, а также на арабском Востоке, откуда проникли в Европу. В 1572 году в «Алгебре» Рафаэля Бомбелли, профессора университета в Болонье, вдруг появляются 143 задачи из «Арифметики» Диофанта. Методы Диофанта обрели новую жизнь только в произведениях двух крупнейших математиков Франции XVI–XVII веков — Франсуа Виета и Пьера Ферма.
Первый этап развития учения о неопределённых уравнениях второго и третьего порядков, начало которому положил Диофант, нашёл своё завершение в работах Леонарда Эйлера [1, c. 39–48].
Итак, сформулируем определение понятия «диофантово уравнение»: линейным диофантовым уравнением называется уравнение с несколькими неизвестными вида 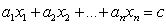 , где коэффициенты
, где коэффициенты 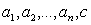 — целые числа, а неизвестные
— целые числа, а неизвестные 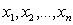 являются целыми или рациональными числами. К решению подобных уравнений сводятся разнообразные текстовые задачи, в которых неизвестные величины выражают количество предметов того или иного рода и поэтому являются натуральными (или неотрицательными целыми) числами. Каждая конкретная задача в целых числах может решаться с помощью разных методов.
являются целыми или рациональными числами. К решению подобных уравнений сводятся разнообразные текстовые задачи, в которых неизвестные величины выражают количество предметов того или иного рода и поэтому являются натуральными (или неотрицательными целыми) числами. Каждая конкретная задача в целых числах может решаться с помощью разных методов.
В настоящее время задача решения неопределенных уравнений формулируется так: пусть дано 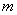 многочленов от
многочленов от 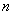 переменных,
переменных, 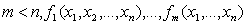 с коэффициентами из некоторого поля
с коэффициентами из некоторого поля 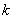 . Требуется найти множество
. Требуется найти множество 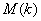 всех рациональных решений системы
всех рациональных решений системы
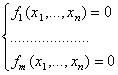 (1)
(1)
и определить его алгебраическую структуру. При этом решение 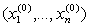 называется рациональным, если все
называется рациональным, если все 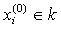 [2, c. 42].
[2, c. 42].
Ограничимся рассмотрением только таких задач Диофанта, которые сводятся к одному уравнению с двумя неизвестными, т. е. к случаю 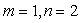 :
:
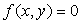 (2)
(2)
Это уравнение определяет на плоскости 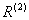 алгебраическую кривую
алгебраическую кривую 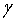 . Рациональное решение (2) будем называть рациональной точкой кривой
. Рациональное решение (2) будем называть рациональной точкой кривой 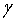 [1, c. 15].
[1, c. 15].
Для диофантовых уравнений имеет место теорема, позволяющая установить наличие корней или же их отсутствие: Неопределенное уравнение второго порядка от двух переменных либо не имеет ни одного рационального решения, либо имеет их бесконечно много, причем в последнем случае все решения выражаются как рациональные функции параметра 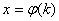 ,
, 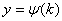 , где
, где 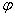 и
и 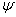 — рациональные функции [1, c. 23].
— рациональные функции [1, c. 23].
При исследовании линейных диофантовых уравнений необходимо ответить на следующие вопросы:
1) имеет ли уравнение целочисленные решения;
2) конечно или бесконечно множество его целочисленных решений;
3) решить уравнение на множестве целых чисел, т. е. найти все его целочисленные решения;
4) решить уравнение на множестве целых положительных чисел;
5) решить уравнение на множестве рациональных чисел [3].
В настоящее время известны следующие способы решения линейных диофантовых уравнений, а именно:
- использование алгоритма Евклида;
- использование цепных дробей;
- способ перебора вариантов;
- использование сравнений [3].
Уравнение второй степени с двумя неизвестными 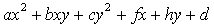 , где
, где 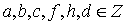 , может:
, может:
1) не иметь решений в целых числах;
2) иметь конечное число решений в целых числах;
3) иметь бесконечное множество решений в целых числах [3, c. 134].
При этом в рациональных числах диофантовы уравнения второй степени либо не имеют решений, либо имеют их бесконечно много.
На данный момент известны следующие способы решения неопределенных уравнений второго порядка, а именно [3]:
- метод полного перебора всех возможных значений переменных, входящих в уравнение;
- метод разложения на множители;
- метод, основанный на оценке выражений, входящих в уравнение;
- метод решения уравнения с двумя переменными как квадратного относительно одной из переменных;
- метод бесконечного (непрерывного) спуска;
- метод, основанный на выражении одной переменной через другую и выделении целой части дроби;
- метод, основанный на выделении полного квадрата.
Далее рассмотрим несколько примеров решения диофантовых уравнений, а именно: метод полного перебора всех возможных значений переменных, входящих в уравнение и метод разложения на множители.
1. Метод полного перебора всех возможных значений переменных, входящих в уравнение.
Пример 1. Найти множество всех пар натуральных чисел, которые являются решениями уравнения 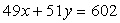
Решение.Выразим из уравнения переменную 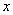 через
через 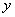 :
: 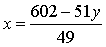 .
.
Так как 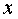 и
и 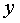 — натуральные числа, то
— натуральные числа, то 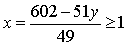 ,
, 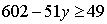 ,
, 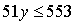 ,
, 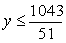 .
.
Показывает перебор вариантов показывает, что натуральными решениями уравнения являются 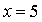 ,
, 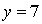 .
.
Ответ: 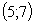 [3, c. 13].
[3, c. 13].
Пример 2. Решить в целых числах уравнение 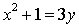 .
.
Решение.
1) Правая часть уравнения делится на 3 при любом целом 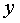 .
.
2) Исследуем, какие остатки может иметь при делении на три левая часть этого уравнения.
По теореме о делении с остатком целое число либо делится на 3, либо при делении на 3 в остатке дает 1 или 2.
Если 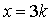 , то левая часть уравнения на 3 не делится.
, то левая часть уравнения на 3 не делится.
Если 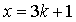 , то
, то
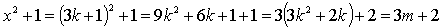 ,
,
следовательно, левая часть уравнения на 3 не делится.
Если 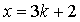 , то
, то
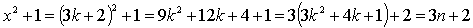 , следовательно, левая часть уравнения на 3 не делится.
, следовательно, левая часть уравнения на 3 не делится.
Таким образом, ни при каких целых 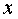 левая часть уравнения на 3 не делится, а правая часть — делится на 3 при любых значениях переменной
левая часть уравнения на 3 не делится, а правая часть — делится на 3 при любых значениях переменной 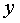 . Следовательно, уравнение в целых числах решении не имеет.
. Следовательно, уравнение в целых числах решении не имеет.
Ответ: решений нет [3, c. 15].
2. Метод разложения на множители.
Данный метод применяется в случаях, когда в уравнениях можно применить какой-либо из способов разложения на множители:
- Формулы сокращенного умножения;
- Вынесение общего множителя за скобку и т. д.
Итак, охарактеризуем метод разложения на множители на конкретных примерах.
Пример 1. Решить уравнение в целых числах 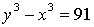 .
.
Решение.Используя формулы сокращенного умножения, разложим правую часть уравнения на множители 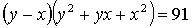 .
.
Выпишем все делители числа 91: 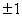 ,
, 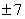 ,
, 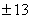 ,
, 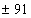 .
.
Проведем исследование: заметим, что для любых целых чисел 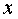 и
и 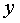 число
число 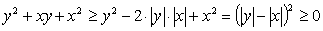 , следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение
, следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение 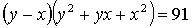 равносильно совокупности систем уравнений:
равносильно совокупности систем уравнений:
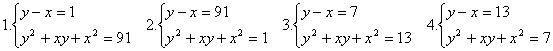 .
.
Решив системы, получим:
1) первая система имеет решения 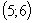 ,
, 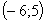 ;
;
2) вторая система решений в целых числах не имеет;
3) третья система имеет решения 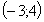 ,
, 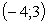 ;
;
4) четвертая система решений в целых числах не имеет.
Пример 2. Найти все целочисленные решения уравнения 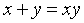 .
.
Решение.Проведем цепочку равносильных преобразований:
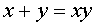 ó
ó 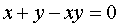 ó
ó 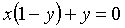 ó
ó 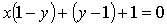 ó
ó 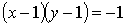 .
.
Так как 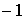 можно представить в виде двух целых чисел с учетом порядка двумя способами, т. е.
можно представить в виде двух целых чисел с учетом порядка двумя способами, т. е. 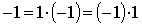 , получаем две системы:
, получаем две системы:
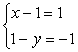 или
или 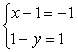 .
.
Решением первой системы является пара 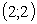 , а второй —
, а второй — 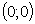 .
.
Ответ: 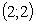 ,
, 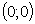 [3, c. 17–19].
[3, c. 17–19].
Оказывается, что некоторые текстовые задачи практического содержания также можно свести к составлению неопределённых уравнений первой и второй степени с двумя неизвестными. Покажем данный прием на конкретных примерах.
Задача № 1
Группу школьников нужно перевезти из летнего лагеря одним из двух способов: либо двумя автобусами типа  за несколько рейсов, либо тремя автобусами типа
за несколько рейсов, либо тремя автобусами типа  за несколько рейсов, причем в этом случае число рейсов каждого автобуса типа
за несколько рейсов, причем в этом случае число рейсов каждого автобуса типа  будет на один меньше, чем рейсов каждого автобуса типа
будет на один меньше, чем рейсов каждого автобуса типа 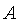 . В каждом из случаев автобусы заполняются полностью. Какое максимальное количество школьников можно перевезти при указанных условиях, если в автобус типа
. В каждом из случаев автобусы заполняются полностью. Какое максимальное количество школьников можно перевезти при указанных условиях, если в автобус типа 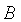 входит на 7 человек меньше, чем в автобус типа
входит на 7 человек меньше, чем в автобус типа 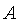 ?
?
Решение.Пусть в автобус типа B входит k человек, а в автобус типа A входит k+7 человек.
Пусть каждый из трех автобусов типа B сделает по m рейсов, а каждый из двух автобусов типа A — по m+1.
Так как в обоих случаях автобусы перевезут одно и то же количество детей, то получим уравнение: 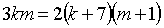 .
.
При k> 14 получаем: 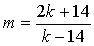 или
или 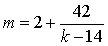 .
.
Число k — 14 — один из восьми делителей числа 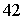 . Перебирая их по очереди, мы получим все возможные решения (8 пар k и m): (14; 44), (16; 23), (17; 16), (20; 9), (21; 8), (21; 5), (35; 4), (56; 3).
. Перебирая их по очереди, мы получим все возможные решения (8 пар k и m): (14; 44), (16; 23), (17; 16), (20; 9), (21; 8), (21; 5), (35; 4), (56; 3).
Для каждой пары последовательно находим количества перевозимых детей, равные 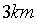 : 1980, 1104, 816, 540, 504, 420, 504.
: 1980, 1104, 816, 540, 504, 420, 504.
Ответ: 1980 детей перевозятся тремя автобусами типа В (по 15 человек) или двумя автобусами типа А (по 22 человека) за 45 рейсов.
Задача 2. Шарики можно разложить в пакетики, а пакетики упаковать в коробки, по 3 пакетика в одну коробку. Можно эти же шарики разложить в пакетики так, что в каждом пакетике будет на 3 шарика больше, чем раньше, но тогда в каждой коробке будет лежать по 2 пакетика, а коробок потребуется на 2 больше. Какое наибольшее количество шариков может быть при таких условиях?
Решение.Пусть в каждой из коробок лежит 3 пакетика, по n шариков в каждом. Во втором случае коробок x + 2, пакетиков в коробке 2, а шариков в пакетике n+ 3. По условию задачи получаем уравнение: 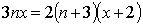 , откуда
, откуда 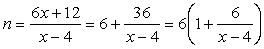 .
.
Заметим, что из 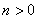 следует, что
следует, что 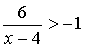 , откуда
, откуда 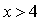 .
.
Учитывая, что числа n и x натуральные, получаем, что 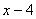 — натуральный делитель числа 36.
— натуральный делитель числа 36.
Количество шариков при этом 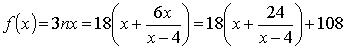 .
.
Решение находим, исследуя функцию 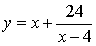 . Данная функция монотонно убывает при
. Данная функция монотонно убывает при 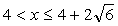 и монотонно возрастает при
и монотонно возрастает при 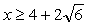 . Следовательно, наибольшее значение функции
. Следовательно, наибольшее значение функции 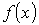 достигается, если
достигается, если 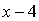 — наибольший или наименьший натуральный делитель числа 36.
— наибольший или наименьший натуральный делитель числа 36.
Если 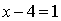 , то
, то 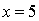 ,
, 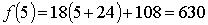 .
.
Если 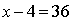 , то
, то 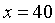 ,
, 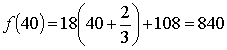 .
.
Ответ: 840 шариков [7, c. 27–28].
Таким образом, решение уравнений в целых и рациональных числах — один из самых красивых разделов математики, теоретические и практические сведения которого используются как в инженерии, биологии, так и повседневной жизни — последние две задачи тому подтверждение. Ни один крупный математик не прошёл мимо теории диофантовых уравнений. Ферма и Эйлер, Лагранж и Дирихле, Гаусс и Чебышев оставили неизгладимый след в этой интереснейшей теории. В настоящее время, в связи с современными требованиями к выпускнику школы, возникает особенная необходимость в изучении неопределенных уравнений. Считаем, что необходимо разрабатывать и составлять элективные и специальные курсы по обучению современных школьников и их учителей основным приемам решения данных уравнений и поиску способов нахождения этих решений, что, безусловно, служит предметом исследования, как математиков, так и методистов.
Литература:
1. Башмакова И. Г. Диофант и диофантовы уравнения. — М.: «Наука», 1972 г.
2. Башмакова И. Г., Славутин Е. И. История диофантова анализа от Диофанта до Ферма. — М.: «Наука», 1984 г.
3. Гринько Е. П., Головач А. Г. Методы решения диофантовых уравнений при подготовке школьников к олимпиадам. — Брест, 2013 г.
4. Жмурова И. Ю., Бесперстова А. Ю. Использование историко-математических сведений в курсе теории чисел // Молодой ученый. — 2013. — № 10
5. Жмурова И. Ю., Коршунова Л. А. Элективный курс «Эйлеровы графы» как средство реализации интеграционных связей математики // Молодой ученый. — 2013. — № 5
6. Корянов А. Г. Математика. ЕГЭ 2010. Задания С6. — Брянск, 2010 г.
7. Шевкин А. В., Пукас Ю. О. ЕГЭ. Математика. Задание С6. — М.: «Экзамен», 2014г.







