Поступающая в ствол реагирующей скважины жидкость начинает охлаждаться в силу существенной разницы температур пласта и расположенных выше горных пород. Контроль за тепловым полем пласта путем замеров температуры на забое добывающих скважин трудоемок из-за необходимости подъема оборудования на период проведения исследований. В то же время замер температуры добываемой жидкости на устье скважины не представляет никакой сложности. Поэтому необходимо установить эмпирическим путем связь между температурами жидкости на забое и устье добывающих скважин [1–7].
С другой стороны, располагая этой связью можно оценить среднее значение температуры нефти в скважине или колонне насосно-компрессорных труб и по ней рассчитать вязкость.
Температуру на забойном участке ниже приема насоса можно замерить спуском термометра сразу после извлечения насосного оборудования из скважины. Длительный период эксплуатации приводит к тому, что температура окружающих горных пород в непосредственной близости к стволу будет соответствовать температуре жидкости на соответствующей глубине скважины. Изменением температуры в период подъема оборудования очевидно можно пренебречь.
Замеренные таким образом температуры жидкости на устье, а также ниже глубины подвески насоса в нереагирующей и реагирующей скважинах показывают, что температура жидкости в нереагирующей скважине изменяется мало — на 2÷3 градуса. В то же время в реагирующей скважине охлаждение жидкости существенно. Наиболее интенсивно охлаждение на забойном участке ствола скважины. Изменение температуры жидкости в НКТ судя по замеренным кривым можно принять линейным.
Зависимость температуры от глубины скважины можно условно разделить на два прямолинейных участка: НКТ и участок между приемом насоса и интервалом перфорации.
С ростом температуры жидкости в интервале перфорации скорость охлаждения жидкости возрастает как на забойном участке, так и в колонне НКТ. Вместе с тем, охлаждение жидкости на забойном участке значительно интенсивнее в силу меньшей скорости подъема флюида и большей теплоотдаче жидкости горным породам при их непосредственном контакте.
В общем случае закономерность распределения температуры по стволу скважины на обоих участках можно схематично представить:
t пр =tу (1+К1 Н)
tзаб =tпр (1+К2 Н) (1)
где:
tу, tпр и tзаб — температуры на устье скважины, приеме насоса и забое скважины;
К1 и К2 — коэффициенты, относящиеся к колонне НКТ и забойному участку соответственно;
Н — текущая глубина скважины.
Обработка результатов замера температур по ряду скважин позволила получить выражения для расчета коэффициентов К1 и К2:
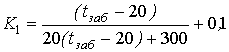 , 0С/м (2)
, 0С/м (2)
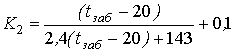 , 0С/м (3)
, 0С/м (3)
Формулы (2) и (3) получены для диапазонов изменения температур на забое скважины 20 ÷ 42,5°С, дебитов скважин 1,5 ÷ 3,6 м3/сут и обводненности нефти 6 ÷ 38 %. Погрешность в расчетах составляет 6,4 %.
Построив графически серию линий распространения температур по глубине скважин можно решать и обратную задачу — по температуре жидкости на устье и глубине подвески насоса рассчитать температуру на забое скважины.
Вопросу температурного режима работы добывающих скважин (нефтяных и гидротермальных) посвящены многочисленные работы, в итоге выполнения которых рассматриваются различные аспекты этого сложного явления. Анализ выполненных исследований показывает, что изучение теплового режима работы добывающих скважин возможно не только аналитически, но и на основе обобщения имеющихся экспериментальных данных. В результате аналитического исследования данного вопроса получено значительное число решений уравнения теплопроводности, описывающего температурные процессы, протекающие. при движении продукции по стволу добывающей скважины.
При теоретических исследованиях принимается, что горные породы в разрезе скважины однородны и изотропны; горные породы залегают горизонтально, а теплопроводные потоки в зоне скважины близки к радиальным при движении в скважине несжимаемой жидкости с постоянным расходом и определенными потерями на трение; отсутствуют фазовые переходы и другие процессы, связанные с выделением или поглощением энергии и т. д.
Тем не менее, во все полученные на сегодня аналитические решения входит ряд трудно определяемых параметров, что существенно сокращает область возможного использования на практике данных решении. Рассмотрим кратко основные физические процессы, происходящие при движении реальной продукции в скважине. Действительно, несмотря на то, что при движении реальной продукции происходит дополнительное выделение тепла за счет необратимых потерь на трение и кристаллизации парафина и солей, а также поглощение тепла при выделении и расширении свободного газа, решения, не учитывающие этих явлений, могут быть использованы, так как при нормальной эксплуатации скважины указанные процессы в тепловом балансе движущегося потока практически скомпенсированы.
В процессе движения продукции от забоя до устья изменение ее температуры за счет теплопередачи колонне труб происходит путем теплопроводности в ламинарном пограничном слое и путем конвекции — в турбулентном ядре. Причем, в зависимости от характеристик ламинарного пограничного слоя и турбулентного ядра изменяется и теплопередача. Так как передача тепла конвекцией протекает несоизмеримо более интенсивно, чем теплопроводностью, изменение температуры в любом поперечном сечении потока должно быть незначительным, что и подтверждается экспериментальными данными.
В ламинарном пограничном слое, хотя и считается, что теплообмен осуществляется теплопроводностью, фактически за счет свободной конвекции возникает массообмен между параллельно текущими слоями жидкости, и теплоотдача увеличивается, хотя остается существенно меньшей, чем в турбулентном ядре. Следует подчеркнуть, что интенсивность теплоотдачи в ламинарном пограничном слое определяется не только теплофизическими характеристиками движущегося потока и твердой стенки, но и толщиной ламинарного пограничного слоя, которая зависит от диаметра трубы, коэффициента гидравлического сопротивления и числа Рейнольдса. Число же Рейнольдса зависит от степени возмущения или стабилизации текущего флюида, возникающих вследствие внешних причин, условий движения флюида в трубе (колебательные процессы, местные сопротивления) и, наконец, вследствие шероховатости стенок трубы не только по ее размерам, но и по форме впадин и выступов. Можно предполагать наличие определенной количественной разницы в процессе теплопередачи при движении сходных потоков флюида по трубам с разным качеством их поверхности вследствие различной чистоты обработки или отложений твердой фазы.
Для стационарного режима работы добывающей скважины действительно могут быть приняты следующие допущения, которые существенно облегчают решение задачи, не приводя к значительным погрешностям [4]:
1. Скважина вертикальная.
2. Горные породы вокруг скважины представлены неограниченным массивом.
3. Горные породы однородны и изотропны.
4. Температура флюида в продуктивном горизонте (пластовая температура tпл) постоянна.
5. Пренебрегаем теплопроводностью вдоль оси скважины, т. к. скорость течения флюида достаточно высока.
6. Пренебрегаем потерями энергии на трение и фазовые переходы, т. к. совокупное проявление этих явлений не нарушает теплового баланса движущегося потока.
Для рассматриваемой задачи уравнение теплопроводности записывается в виде [5]:
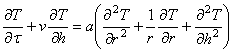 , (4)
, (4)
где T — температура, К;
τ — время,с;
h — вертикальная координата, м;
v — скорость движения флюида, м/с;
r — радиальная координата (радиус), м;
а — коэффициент температуропроводности, м2/с;
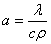 , (5)
, (5)
λ — коэффициент теплопроводности, Вт/м·град;
с — удельная теплоемкость флюида, Дж/кг·град;
ρ — плотность флюида, кг/м3.
Так как рассматривается стационарный процесс, то первое слагаемое в левой части (4) равно нулю. С учетом этого и принятых допущений перепишем (5) так:
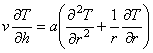 . (6)
. (6)
Все известные решения (6) могут быть приведены к следующему виду (с точностью до постоянного числового коэффициента в последнем слагаемом правой части):
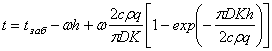 , (7)
, (7)
где tзаб — температура на забое скважины (пластовая температура), °С;
ω — геотермический градиент, град/м;
q — объемный расход жидкости, м3 /с;
D — внутренний диаметр канала, м;
К — коэффициент теплопередачи в скважине, Вт/м2· град.
Умножим сомножитель перед скобками в третьем слагаемом и показатель экспоненты в (7) на 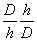 :
:
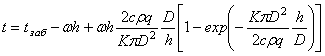 . (8)
. (8)
Разложим показательную функцию в (7) в степенной ряд и, ограничиваясь тремя первыми членами разложения, получим:
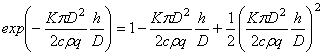 . (9)
. (9)
С учетом (8) выражение (7) после необходимых сокращений приводится к виду:
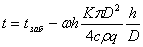 . (10)
. (10)
Полученная зависимость, являясь решением уравнения теплопроводности, может использоваться для расчета распределения температуры по глубине добывающей скважины.
Геотермический градиент ω можно рассчитать по следующей формуле:
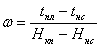 , (11)
, (11)
где tпл, tнс — соответственно пластовая температура и температура нейтрального слоя, °С;
Нкп, Hнс — соответственно расстояние от поверхности земли до кровли продуктивного пласта и до нейтрального слоя, м.
Температура нейтрального слоя для некоторых нефтяных регионов следующая: Коми Республика — 4°С; Западная Сибирь — 5°С; Урало-Поволжье — 6°С; Белоруссия и Украина — 9°С; Краснодарский край, Чечня и Ингушетия — 13,5°С; Азербайджан, Казахстан и Средняя Азия — 16°С. Расстояние до нейтрального слоя от поверхности земли изменяется от 20 до 40 м и может быть принято, в среднем, равным 30 м [7].
Гидродинамическое и тепловое подобие потоков возможно при соблюдении критериев Рейнольдса Re, Прандтля Pr и Нуссельта Nu
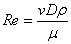 , (12)
, (12)
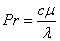 , (13)
, (13)
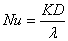 . (14)
. (14)
Взаимосвязь вышеприведенных критериев учитывается критерием Стантона St:
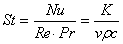 , (15)
, (15)
где v — скорость движения жидкости, м/с,
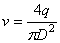 , (16)
, (16)
μ — вязкость жидкости, Па·с.
Подставляя (16) в (15), получим:
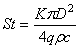 . (17)
. (17)
Заменим часть второго слагаемого правой части выражения (10) соответствующим значением (17) и запишем:
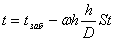
или
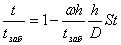 . (18)
. (18)
Данное выражение является уравнением распределения температуры по глубине скважины в безразмерном виде.
В полученных решениях (10) и (18) неизвестным остается коэффициент теплопередачи. К. Этот коэффициент зависит от большого количества факторов, которые в практической деятельности не всегда могут быть известными. Несмотря на значительное количество, в основном, аналитических исследований, промысловые инженеры не имеют простых и достаточно точных рекомендаций по его определению. В то же время, как это видно из (18), обобщение температурных режимов работы добывающих скважин может быть выполнено с использованием критерия Стантона. Знание же температуры не только в любой точке скважины, но даже на устье при известной температуре на забое скважины сегодня представляет несомненный практический интерес.
Литература:
1. Казак А. С. Технология и техника эксплуатации скважин с тяжелой высоковязкой нефтью // Тематич. научн.-техн. обзор: Сер. Нефтепромысловое дело. М.: ВНИИОЭНГ, 1979. С.44.
2. Рахматуллин В. Н., Валеев М. Д. Добыча тяжелой нефти Шафрановского месторождения // Нефтепромысловое дело и транспорт нефти / Научн.-техн. информ. сб. М.: ВНИИОЭНГ, 1985. № 3. С. 15–16.
3. Сейтпагамбетов Ж. С. Геотехнические и термические методы повышения нефтеотдачи пластов // Труды Международной научной конференции «Наука и образование — ведущий фактор стратегии «Казахстан -2030». Караганда, 2000. С. 670–672.
4. Мищенко И. Т. Скважинная добыча нефти. Москва, 2003.
5. Сахаров В. А., Мохов М. А. Гидродинамика газожидкостных смесей в вертикальных трубах и промысловых подъемниках. Москва, 2004.
6. Щуров В. И. Технология и техника добычи нефти. Москва, 2005.
7. Справочное руководство по проектированию разработки и эксплуатации нефтяных месторождений. Добыча нефти. Москва, 2005.







