В работе изучается поле динамических напряжений и смещений возникающее в близи цилиндрического тела произвольной плотности в упругой средств при прохождении плоской волны расширения. Получено численные результат на основе метода Гаусса и специально к функций.
Бу ишда зичлиги ихтиёрий бўлган цилиндрик жисмда ва унинг атрофида таъсирида ҳосил бўладиган кучланиш ва деформация ҳолати ўрганилган. Қўйилган масала махсус функциялар ва Гаусс усули ёрдамида ечилади ва сонли натижалар олинди.
В случае достаточно протяженных подземных сооружений и воздействия, направленного перпендикулярно ее продольной оси, окружающая среда и обделок сводятся к плоской задаче динамической теории упругости (или вязко упругости).В предположении обобщенного плоско деформированного состояния уравнение движения в смешениях имеет вид [1]
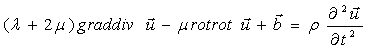 , (1)
, (1)
где 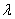 и
и 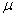 — модули упругости, называемыми постоянными Ламе;
— модули упругости, называемыми постоянными Ламе; 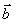 - вектор плотности объемных сил
- вектор плотности объемных сил 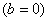 ; r — плотность материала,
; r — плотность материала, 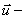 вектор смешения, который зависит от
вектор смешения, который зависит от 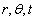 . На внутренний
. На внутренний 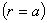 и внешний
и внешний 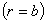 груния цилиндрического должны удовлетворяться следующие условия. Поставленная задача решается в потенциалах перемещений:
груния цилиндрического должны удовлетворяться следующие условия. Поставленная задача решается в потенциалах перемещений:
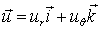 ;
; 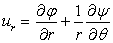 ;
; 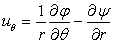 .
.
Потенциалы 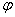 и
и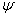 удовлетворяют волновому уравнению
удовлетворяют волновому уравнению
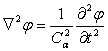 ;
; 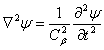 , (2)
, (2)
где 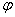 и
и 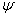 — являются потенциалами перемещений,
— являются потенциалами перемещений, 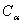 и
и 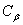 - фазовые скорости распространения волн расширения и сдвига. В работе [1] показано, что жидкость можно считать идеальной, а ее движение безвихревым и изотермическим. При давлениях до 100 МПа движение жидкости полнее удовлетворительно описывается волновыми равнениями для потенциалов скорости частиц жидкости [2]
- фазовые скорости распространения волн расширения и сдвига. В работе [1] показано, что жидкость можно считать идеальной, а ее движение безвихревым и изотермическим. При давлениях до 100 МПа движение жидкости полнее удовлетворительно описывается волновыми равнениями для потенциалов скорости частиц жидкости [2]
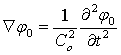 ,
,
где С0- скорость звука в жидкости. Потенциал φ0 и вектор скорости жидкости 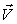 связаны зависимостью
связаны зависимостью 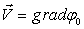 . Давление жидкости можно определить с помощью линеаризованного интеграла Коши-Лагранжа
. Давление жидкости можно определить с помощью линеаризованного интеграла Коши-Лагранжа 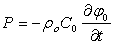 , где ρ0- плотность жидкости. При условии безотрывного обтекания жидкости нормальная компонента скорости жидкости и оболочка на поверхности их контакта должны быть равны, т. е.:
, где ρ0- плотность жидкости. При условии безотрывного обтекания жидкости нормальная компонента скорости жидкости и оболочка на поверхности их контакта должны быть равны, т. е.:
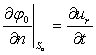 ,
,
где S0- поверхность контакта; n-нормальные поверхности оболочки; ur — перемещения оболочки по нормали. Падающая плоская волна расширения (или сдвига) рассматривается распространяющейся в положительном направлении оси х и представляется следующим образом:
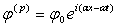 ;
; 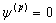 ; или
; или 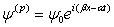 ;
; 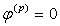 ,
,
где 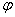 0 или
0 или 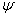 0 –величины амплитуды; ω- круговая частота;
0 –величины амплитуды; ω- круговая частота; 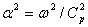 и
и 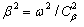 -волновые числа расширения и сдвига соответственно. Если граница области, в которой изучается волновое поле уходит в бесконечность, тогда требуются дополнительные условия в бесконечности и подробно обсуждены в работах [1,2]
-волновые числа расширения и сдвига соответственно. Если граница области, в которой изучается волновое поле уходит в бесконечность, тогда требуются дополнительные условия в бесконечности и подробно обсуждены в работах [1,2]
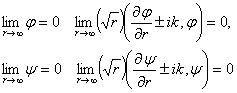 (3)
(3)
Если функция 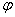 удовлетворяет уравнению Гельмгольца (в нашем случае удовлетворяет), то однозначность решения задачи в бесконечной области можно обеспечить требованиям (3). Здесь r радиус в цилиндрической системе координат. На границе двух тел, выполняется условие жесткого контакта, т. е. выполняется условие равенства соответствующих перемещений и напряжений:
удовлетворяет уравнению Гельмгольца (в нашем случае удовлетворяет), то однозначность решения задачи в бесконечной области можно обеспечить требованиям (3). Здесь r радиус в цилиндрической системе координат. На границе двух тел, выполняется условие жесткого контакта, т. е. выполняется условие равенства соответствующих перемещений и напряжений:
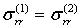 ;
; 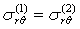 ;
; 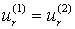 ;
; 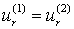 .
.
Одна из задач посвящена распространению гармонических сдвиговых волн в двумерном упругом теле с круглым отверстием (подкрепленным). В такой постановке изучается наложение подходящих волн и отраженных от отверстия волн сдвига и растяжения — сжатия, что приводит к концентрации напряжения. Решение дифракционной задачи для плоской гармонической сдвиговой волны получено в [1], который имеет следующий вид (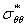 =
=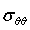 / s0; sq=mb2y0; y0 — амплитуда падающих волн, m — коэффициент Ламе)
/ s0; sq=mb2y0; y0 — амплитуда падающих волн, m — коэффициент Ламе)
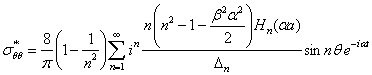
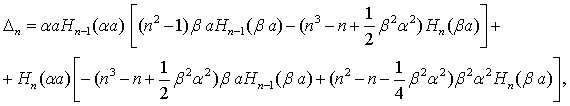 где Hn(ba) — функция Ханкеля; a = w/Cp; b = w/CS; Cp и CS — соответственно скорости распространения продольных и поперечных волн; w — круговая частота, p = 3,14. Расчеты методами теории упругости дают при отсутствии обделки вокруг отверстия и длине волны существенно большей диаметра отверстия, следующее приближенное выражение для напряжений по периметру:
где Hn(ba) — функция Ханкеля; a = w/Cp; b = w/CS; Cp и CS — соответственно скорости распространения продольных и поперечных волн; w — круговая частота, p = 3,14. Расчеты методами теории упругости дают при отсутствии обделки вокруг отверстия и длине волны существенно большей диаметра отверстия, следующее приближенное выражение для напряжений по периметру:
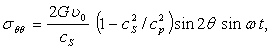
где G — модуль сдвига для грунта, u0 — амплитуда скорости падающий сейсмические волны. Ввиду того, что длинные сейсмические волны, как правило, превышают характерные размеры поперечных сеченый выработок (например, диаметр D), особы интерес представляет решение дифракционных задач для длинноволновых воздействий, т. е. когда 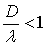 . При больших длинах волн (
. При больших длинах волн (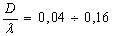 ) максимальные коэффициенты динамических концентраций оказалась на 5–10 % больше, чем при соответствующем двуосном статическом нагружении (λ→¥) [1]. При
) максимальные коэффициенты динамических концентраций оказалась на 5–10 % больше, чем при соответствующем двуосном статическом нагружении (λ→¥) [1]. При 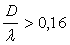 динамические концентрации напряжений существенно ниже статических. Представленные числовые результаты показывает, что в отличие от случая жесткого включения [1], величина Кs очень сильно зависит от
динамические концентрации напряжений существенно ниже статических. Представленные числовые результаты показывает, что в отличие от случая жесткого включения [1], величина Кs очень сильно зависит от 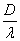 . Это различия можно отнести к возможности распространения обобщённых волн типа Релея на вогнутой свободной цилиндрической поверхности полости. Учет вязких свойств материала окружающей среды при расчета на действие сейсмических волн, снижает напряжения и перемещения на 10–15 %.
. Это различия можно отнести к возможности распространения обобщённых волн типа Релея на вогнутой свободной цилиндрической поверхности полости. Учет вязких свойств материала окружающей среды при расчета на действие сейсмических волн, снижает напряжения и перемещения на 10–15 %.
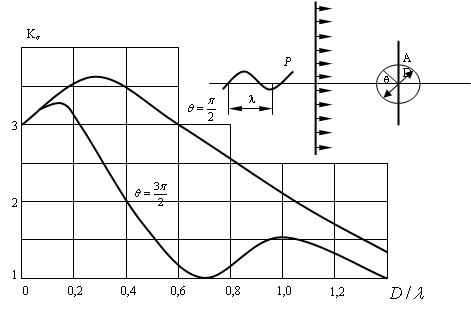
Рис. 1. Зависимость коэффициента концентрации напряжения от длины волны
Расчеты показывают, что при фиксированных значениях амплитуды и длительности действия падающей волны с увеличением акустических параметров жидкости, прогибы и усилия также увеличиваются. В области длинных волн распределения напряжения трубы с жидкостью и без жидкости отличаются до 15 %, а в области коротких волн в некоторых значениях частоты они отличается до 40 %.
Полученные численные результаты позволяют сделать следующие выводы:
- явление местного резонанса проявляется более сильно для сейсмического воздействия в виде SV — волны, чем Р — волны.
- наличие воды в трубах увеличивает сейсмическое воздействие на них на 10–20 %.
- чем плотнее грунт насыпи, тем меньше сейсмическое воздействие на подземные трубы. При 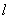 >10D динамическая задача сводится к квазистатической.
>10D динамическая задача сводится к квазистатической.
- изменение толщины стенки и класса бетона практически не влияет на динамическое давление грунта на железобетонные трубы при сейсмическом воздействии. Можно отметить, что проектирование оптимальной обделки с учетом влияния динамической нагрузки требует в общем случае, кроме обычного выбора толщины и конструкционного материала, согласования последнего со свойствами окружающего горного массива.
Литература:
1. Рашидов Т. Р. Динамическая теория сейсмостойкости сложных систем подземных сооружений.- Ташкент. Фан.1973.-182с.
2. Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. СО РАН, Новосибирск, 1966.- 188с.
3. Рашидов Т. Р., Хожиметов Г. Х., Мардонов Б. М. Колебания сооружений, взаимодействующих с грунтом. – Ташкент. Фан. 1975.-174с.







