Применение систем компьютерной математики и компьютерных технологий при изучении дисциплин высшей математики как один из видов педагогических технологий

В статье рассматриваются стратегические ориентиры создания новых  программ высшего математического образования для экономистов, обусловленные вызовами современного постиндустриального общества. Рассмотрены пути профессио­нально-ориентированного обучения с помощью компьютерных технологий в рамках концепции компетентностного подхода к формированию руководителей высшего, среднего и низшего звена, знакомых с компьютерными технологиями  решения  задач во всех сферах экономики, а также в международном бизнесе.

1. Системы компьютерной математики, их структура, задачи и основные характеристики

            Одним из приоритетных направлений развития экономики и образования в современном мире является применение компьютерных технологий.

   Учет этого объективного фактора  требует от  ВУЗов обучать и выпускать руководителей высшего, среднего и низшего звена, знакомых с компьютерными технологиями  решения  задач во всех сферах экономики, а также в международном бизнесе. В свою очередь от преподавателей  ВУЗов сегодня требуется не только умение обучать  с   использованием классических форм преподавания, но также создавать и осваивать новые способы изучения предметов с применением компьютеров и компьютерных технологий.

            Компьютерная математика – это новое направление в математике, появившееся на пересечении классической математики и информатики. Оно возникло на рубеже нового столетия и связано с успехами внедрения персональных компьютеров (ПК) в практику решения математических задач.

    Главным средством компьютерной математики стали системы компьютерной математики (СКМ). Они дают возможность использовать математические методы без процедуры программирования и тем самым создают любому бухгалтеру, банковскому служащему, экономисту-аналитику удобную для их работы среду.

    Признанными мировыми лидерами из числа универсальных математических систем  являются пять:

Derive (Corp. Texas Instruments Ins.,USA), Maple (Corp.MapleSoft, Canada),

 Mathcad (MathSoft Ins.,USA), Mathematica (Wolfram Research Ins., USA),

Matlab (Mathworks Ins., USA).

Общими признаками систем  этого класса считаются:

1) объединение аналитических и численных методов вычислений;

2)  использование языков высокого уровня;

3) визуализация результатов вычислений;

4) возможность обмена информацией между собой с помощью различных форматов.

Следует заметить, что все они совместимы с операционными системами  Windows , широко используемыми в банковском деле, бухгалтерии и других отраслях экономики. 

   По своему содержанию СКМ – это особый вид программ, реализуемых на ПК и предназначенных для решения широкого круга математических задач.

Принципиальная структурная схема СКМ приведена на рис. 1.

Основу системы компьютерной математики составляет представительный набор базовых функций и алгоритмов, так называемых  встроенных функций, образующих ЯДРО системы. С помощью подготовленных программ осуществляются быстрые вычисления всех функций ядра.

 Количество встроенных функций в ядре системы компьютерной математики может составлять от нескольких сотен (Derive 6) до  нескольких тысяч (Maple, Mathematica), что отображено на диаграмме 1.1.

Диаграмма 1.1

 

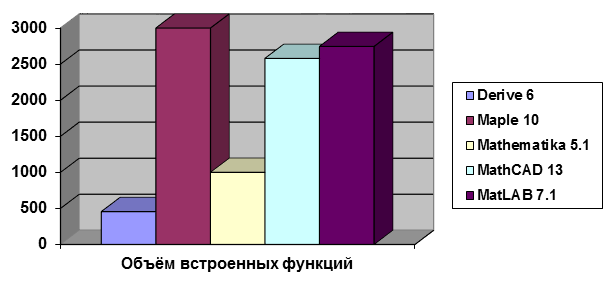
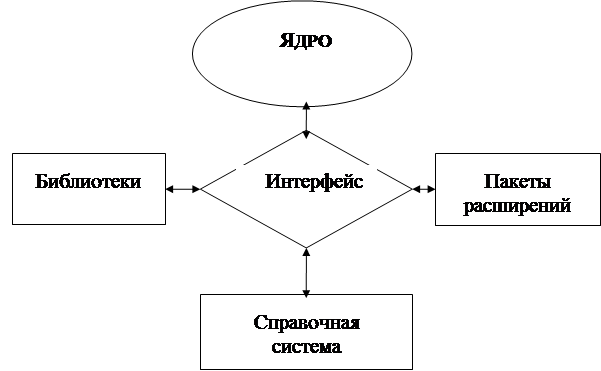
Рис. 1. Принципиальная структурная схема универсальных СКМ

 

Для вычислений редких функций и процедур  вне ядра создаются БИБЛИОТЕКИ. Наращивание вычислительных возможностей системы достигается также за счет ПАКЕТОВ РАСШИРЕНИЯ. Такие пакеты может писать сам пользователь на языке программирования системы компьютерной математики, что обеспечивает большую адаптацию системы к решаемым задачам.

ИНТЕРФЕЙС современных СКМ обычно базируется на операционной системе WINDOWS и, следовательно, является типичным для Windows-приложений.

Любая из существующих СКМ содержит в своем составе в большей или меньшей степени огромный математический аппарат и объем знаний в области математики.  Поэтому такие системы могут не только обеспечить решение прикладных задач, но и могут служить практически неисчерпаемой и  быстро доступной библиотекой математических знаний, накопленных за многие века.

В области высшей математики СКМ решают следующие основные задачи:

Раздел 1.  Математический анализ:

·         вычисление пределов функций;

·         дифференцирование выражений;

·         поиск экстремумов функций;

·         интегрирование функций;

·         решение дифференциальных уравнений;

·         вычисление сумм и произведений рядов;

·         разложение функций в ряд Тейлора и др.

Раздел 2.  Линейная алгебра:

·         решение систем линейных уравнений;

·         выполнение операций с векторами и матрицами;

·         вычисление собственных значений и собственных векторов матриц;

·         решение задач линейного программирования и др.

Раздел 3.  Аналитическая геометрия:

·         вычисление элементов треугольника;

·         определение уравнений плоскостей в трехмерном пространстве

·         кривые второго порядка.

Раздел 4.  финансовая математика:

·         разовые платежи;

·         поток платежей.

         Кроме задач перечисленных разделов СКМ решают также основные задачи аналитической геометрии, теории вероятностей и математической статистики и др..

Современные универсальные  СКМ во всем мире получили широкое применение, прежде всего в образовании и науке. В сфере образования применение СКМ способствует повышению фундаментальности математического образования и сближению отечественной системы образования с западной.

           Современные версии основных систем компьютерной математики, их разработчики, а также сложившиеся к настоящему времени оценки применения этих систем в образовании и науке представлены в таблице 1.

Таблица 1.

Системы компьютерной математики	Фирма разработчик	Применение в образовании и науке
Derive 6	Texas Instruments, Dallas,USA	Изучение математики на первых курсах ВУЗов нематематического профиля, а также в школах. Система достаточно простая в изучении, надёжная и дешевая.
Maple 10	Waterloo Maple Ins., Canada	Университетское образование и научные исследования. Уникальное ядро символьных вычислений. Развитая графика и средства форматирования.
Mathematika 5.1	Wolfram	Высшее образование и научные исследования. Содержит методы теории графов, линейного программирования и др. Уникальная трехмерная графика.
MathCAD 13	MathSoft	Универсальное применение и высокая популярность. Подготовка научных отчётов, книг и других документов.
MatLAB 7.1	MathWork	Университетское образование с техническим уклоном. Научные исследования с численным моделированием. Развитые матричные средства.

 

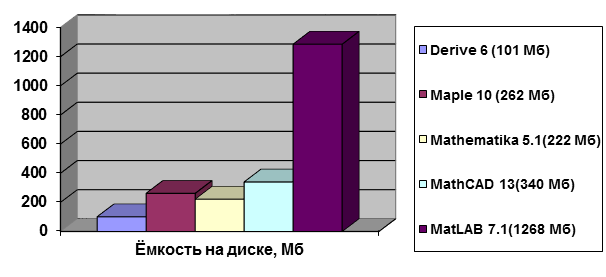
На диаграмме 1.2 приведены ёмкостные характеристики современных систем компьютерной математики.

Диаграмма 1.2

2. Компьютерная графика как новое средство визуализации математических понятий

Системы компьютерной математики решают также задачи графической визуализации результатов вычислений, в том числе построение:

·         графиков функций в декартовой, полярной системе координат и графиков функций в параметрической форме;

·         графиков трехмерных поверхностей;

·         контурных, векторных и других специальных графиков;

·         анимированных графиков с их воспроизведением.

Графика систем СКМ является новым и достаточно эффективным средством визуализации математических понятий, что способствует их лучшему восприятию и усвоению.

Эффект и новизна компьютерной визуализации основаны на способности СКМ мгновенно формировать график функции.

После ввода функции и выдачи соответствующей команды СКМ немедленно строит график функции. Это свойство СКМ позволяет при изучении функций произвольно изменять любой параметр отображаемой функции и одновременно наблюдать, как это сказалось на графике функции.

График функции одной переменной и графики ее первой и второй производных на одном экране позволяют понять качественную связь между ними, в  том числе условия существования точек экстремума и точек перегиба, условия возрастания и убывания функции и др.

На рис. 2. связь функции, и ее первых двух производных показана на примере простейшей функции  y = x³.  Графики функции, и ее первой и второй производной обозначены соответственно – 0;1;2.

 

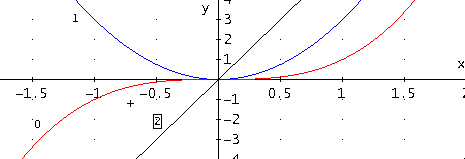
Рис. 2. Графики: функции (0), ее первой (1) и второй (2) производной

 

Компьютерная графика является незаменимым дополнительным средством для визуализации и усвоения понятия сходимости степенных рядов. Удерживая в разложении функции в ряд Тейлора различное количество членов и создавая одновременно на экране графики таких выражений, можно наглядно видеть степень близости различных разложений к самой функции.

На рис. 3 приведены графики функции sinx и ее разложений в ряд Маклорена с удержанием одного – x, двух – ( x – x³ /6 ) и трех членов – ( x – x³/ 6 + x⁵/ 120 ). Графики на рисунке обозначены соответственно– 0, 1, 2, 3. Для иллюстрации сходимости ряда выбран диапазон изменения  x  от  –4 до  +4, т.е. близко к основному периоду функции.

 

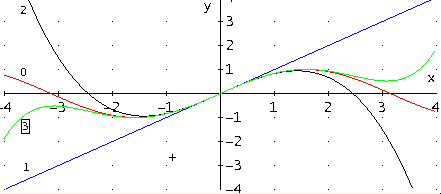
Рис. 3. Графики функции sinx и ее разложений в ряд Маклорена

 

Из рисунка видно, как с увеличением количества членов в разложении и уменьшением значений аргумента графики разложений приближаются к графику исходной функции.

Большие трудности при изучении функций двух переменных вызывает наглядное представление сложных трехмерных поверхностей.

Система Derive решает и эту задачу, создавая наглядный пространственный образ математических выражений с двумя переменными. При этом свойство системы вращать график и фиксировать его произвольное положение позволяет всесторонне и детально изучить закономерность, описываемую функцией.

3. Математический практикум на основе системы Derive

В системе изучения высшей математики в Академии практикум по математике на основе системы Derive может рассматриваться как завершающий этап обучения после традиционного изучения основных дисциплин: «Линейной алгебры», «Математического анализа», «Аналитической геометрии» и «Финансовой математики».

            Основными целями проведения практикума являются:

1.Овладение студентами основами компьютерных технологий решения основных задач линейной алгебры и математического анализа.

2.Углубление и расширение знаний математических методов этих дисциплин, повышение фундаментальности математического образования.

3.Приобретение навыков экономических исследований с использованием методов высшей математики и возможностей компьютерной системы Derive.

Кроме отмеченных выше, цель практикума состоит также в том, чтобы научиться решать задачи математики не «вручную» на бумаге, как это было в прошлом, а с использованием современного интеллектуального технического средства – компьютера.

Выбор системы Derive  для проведения практикума обусловлен следующими соображениями.

            Во-первых, из всех известных и широко используемых в настоящее время универсальных математических систем, например,Maple, Mathcad, Matlab и др. система Derive является самой малой и одновременно уникальной системой, способной эффективно решать разнообразные математические задачи с высокой достоверностью и корректностью.

            Во-вторых, в области образования Derive считается наиболее простой в освоении и самой популярной системой начального уровня математического образования с ориентацией на студентов первых курсов ВУЗов и школьников.

            В-третьих, система Derive не требует от компьютера сколько-нибудь значительных ресурсов и может быть установлена на любом современном компьютере.

Прохождение практикума предполагает чтение лекций и практику решения задач в компьютерных классах с использованием последней версии системы Derive 6 и отдельного приложения с вариантами индивидуальных заданий для студентов.

Полученный опыт проведения такого практикума на факультете бизнеса и делового администрирования показывает, что необходимый объем аудиторных занятий укладывается в одном учебном модуле: 16 часов лекций и 36 часов практических занятий в компьютерных классах (18 занятий по 2 часа каждое). Таким образом, всего 52 часа.

Наблюдение за студентами во время проведения практикума свидетельствует о появлении у них повышенного интереса к изучению профессио­нально-ориентированной математики.

Практикум на основе Derive 6 позволяет студентам решать задачи большой размерности, помогает им развить геометрическое воображение, освобождает много времени, которое можно потратить на решение собственно экономических проблем.

 

ЛИТЕРАТУРА

1. Пучков В.И., Филиппова Н.В., Быканова О.А., Кислов В.И. Практикум по    математике     с использованием компьютерной системы DERIVE . М. Изд-во, Рос. экон. акад.,2006.
2. Половко А.М. Математическая система DERIVE для студентов. «БХВ – Петербург». СПб.,2005.
3. Дьяконов В.П. Система компьютерной алгебры DERIVE. Самоучитель и руководство пользователя. СОЛОН – Р. М., 2002.
4. Дьяконов В.П., Новиков Ю., Рычков В. Самоучитель. Компьютер для         студента.  «Питер». СПб.,2000.
5. Лобанова О.В. Практикум по   решению задач в  математической системе DERIVE.Финансы и статистика. М.,1999.
6. Практикум по  математике для экономистов. Под ред. проф. Крамер Н.Ш. ЮНИТИ. М., 2005.
7. Пучков В.И., Филиппова Н.В., Быканова О.А., Практикум по    математике     с использованием компьютерной системы DERIVE . М. Изд-во, Рос. экон. акад.,2008.

8.      Kutzler B., Kokol-Volic V. Introduction to DERIVE 6. Hagenberg: Soft Warehouse GmbH&CoKG ISBN3-9500364-5-8, 2003.

9.      Kutzler B., Kokol-Volic V. DERIVE 6 Reference Guide. Hagenberg: Soft Warehouse GmbH&CoKG ISBN3-9500364-7-4, 2003.