При разработке наукоемких методологий для начальных этапов поиска решений трудных, нестандартных практических задач, содержащих трудно формализуемые и высокие требования к качеству управления (оценивания, прогнозирования), основную роль играет системный подход (идентификация, математические и вычислительные проблемы управления, развитие информационно-вычислительной среды) [1…5].
Обычно конкретные математические и прикладные исследования часто опережаются и подсказываются интуицией, в том числе математической. Применение математического аппарата определяется степенью его разработанностиидостаточности для отыскания решения практических проблем операциональных возможностей. При поиске решения практической проблемы иногда целесообразнее использовать непараметрические условия, чем параметрические. Абстрактность и отсутствие наглядности основных математических понятий (иногда сильно отличающихся от естественных для человека базисных понятий), требуют создания специальных возможностей перехода от явлений реального мира в виртуальный мир математической теории и обратно из виртуального — в объективную реальность (идентификации). Любая методология, естественно, содержит человеческий выбор в текущем процессе идентификации.
Поиск адекватного семейства математических моделей (альтернатив) для параметрической или непараметрической идентификации фактически является структурной идентификацией. К сожалению, пока нет четкого понимания терминов поиск и адекватность; нет общепризнанного толкования их смысла и детально разработанных трактовок. Поиск на предметно-содержательном (наглядном) уровне обычно осознается как сложная интеллектуальная деятельность с доминирующей ролью технологических и теоретических знаний, интуиции, здравого смысла и опыта субъекта идентификации (целостный наглядный образ реальных процессов выражается на языке выбранного метода идентификации). На концептуальном (объяснительном) уровне считается, что в процессе структурной идентификации существенную роль играют интуиция и жизненный опыт лица, принимающего решение. На уровне конкретного теоретического исследования основные интеллектуальные усилия направляются на структуризацию и абсолютную формализацию данного процесса. В рамках математического дисциплинарного образанаиболее важны теоретические исследования по разработке алгоритмов генерации и перебора структур (заданное семейство математических уравнений), выбор и оценка качества наилучшей структуры.
Не менее сложная ситуация связана со словом адекватность. В настоящее время содержанием математической теории структурной идентификации является математическое моделирование и исследование актуальных проблем локальных фрагментов без учета их реального контекста (их учет возможен при наличии отображения всего наглядного образа на дисциплинарный уровень при разработанных математических основах структурной идентификации). Структурная идентификация предполагает:
- математический выбор типа ковариационной матрицы выхода многомерной системы,порядков дискретных динамических моделей на основе ранговых критериев, типа модели нелинейного динамического объекта;
- оценивание достоверности результатов при использовании различных методов практической идентификации;
- переход от идеи к адекватной математической задаче;
- локальную и глобальную идентифицируемость типа модели в пространстве состояний;
- автоматизацию процессов структурной и параметрической идентификации;
- математический выбор типа моделей нелинейной системы (из нескольких семейств нелинейных дифференциальных уравнений при различных входных процессах и воздействиях);
- многомерный статистический контроль технологического процесса по регрессионным остаткам и др.
Интуиция, жизненный опыт и здравый смысл, как уже отмечалось, признаются в качестве основных инструментов субъекта структурной идентификации (доминирование творческих способностей человека над ценностью современного теоретического знания).
Допускаются различные типы структурной идентификации; основными ее этапами являются:
- разработка содержательной постановки практической задачи,
- выбор математической задачи с заданными параметрами,
- поиск адекватных значений заданныхпараметров математической задачи,
- коррекция содержательной постановки практической задачи,
- предварительный выбор и алгоритмизация адекватной постановки,
- поиск решения пробнойпостановки практической задачи и др.
Таким образом, идентификация рассматривается как процесс получения знания для внедрения в практику методов математики.
В качестве иллюстрации рассмотрим приложения диаграммы и принцип Парето (начальные 20 % определяют последующие 80 % времени выхода контролируемого параметра на эксплуатационное значение) для управления качеством строительных материалов. А именно, формирования требуемых структуры и свойств эпоксидных композитов (ЭК) повышенной плотности для защиты от радиации (использовались отходы стекольной промышленности с большим содержанием свинца) [6,7].
Для случая скалярного управления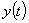 
при оптимизации (с точки зрения требуемых характеристик кинетических процессов формирования отдельных физико-механических характеристик (свойств) материала) использовался функционал
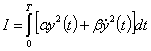
В частном случае при a = 1, b = 0
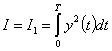
и оптимизация обеспечивает перевод объекта из начального в конечное состояние на промежутке [0, Т] сминимальной энергией управления.
Учитывая, что управление структурой и свойствами материала осуществляется изменением соответствующих рецептурно-технологических параметров, естественным является подход к синтезу материалов как к задаче управления[6,7].
Обычно структура композита в большей степени зависит от скорости расхода энергии, чем от ее величины, сообщенной системе. В связи с этим наряду с I1 рассматривался функционал
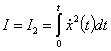
и кумулятивная кривая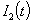 
.
Как оказалось, для всех основных кинетических процессов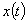 
, tÎ [0, Т] выполняется условие
,
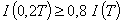что подтверждает возможность использования принципа Парето при оценке формирования физико-механических характеристик материалов. А именно, структура и свойства материала на 80 % определяются начальными 20 % длительности выхода контролируемого параметра на эксплуатационное значение.
На рис. 1 приводится кинетический процесс 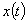и соответствующие кумулятивные кривые тепловыделения (из сравнения кумулятивных кривых I1(t)иI2(t)следует, что при использовании диаграмм Парето необходимо исходить из функционала I2).
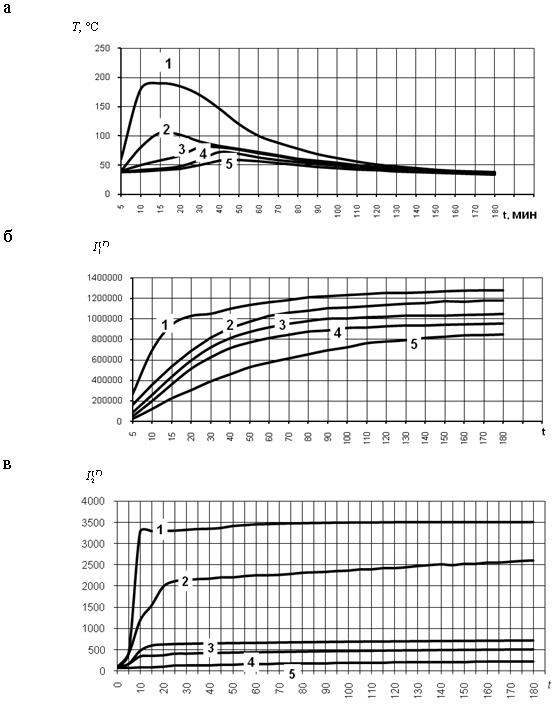
Рис.1. Зависимость температуры саморазогрева при полимеризации эпоксидного композита,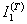 
и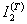 
от t, мин: 1 — ненаполненная смола; 2 — П/Н = 1/5; 3 — П/Н = 1/10; 4 — П/Н = 1/15; 5 — П/Н = 1/20
Литература:
1. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.
2. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. –2013. — № 5. — С. 42–45.
3. Гарькина И. А., Данилов А. М. Опыт разработки композиционных материалов: некоторые аспекты математического моделирования / Известия ВУЗов. Строительство. — 2013. -№ 8 (656). — С.28–33.
4. Данилов А. М., Гарькина И. А., Жегера К. В. Математическое программирование в управлении качеством материалов // Региональная архитектура и строительство. № 1(18), 2014. — C. 30–37
5. Гарькина И. А., Данилов А. М., Прошин И. А. Опыт разработки материалов с позиций системного анализа / XXI век: итоги прошлого и проблемы настоящего (плюс) Серия: технические науки. Машиностроение и информационные технологии. — № 12(16). — 2013. С. 219–225.
6. Гарькина И. А., Данилов А. М. Управление качеством материалов со специальными свойствами / Проблемы управления. — 2008. -№ 6. -С. 67–74.
7. Гарькина И. А., Данилов А. М., Королев Е. В. Когнитивное моделирование при синтезе композиционных материалов как сложных систем / Известия вузов. Строительство. — 2009. -№ 3/4. — С.30–37.
