Ключевые слова: нейронные сети, прогнозирование, моделирование, энергопотребление
Введение. В настоящее время на предприятиях осуществляется контроль различных показателей электрическими средствами, с помощью химического или физического анализа и т. д. От способа измерения зависит дискретность контроля и своевременность получения значений. В случае прогнозирования энергопотребления необходимо иметь данные о таких характеристиках как температура и потребляемая мощность за один час. Рассматриваемые характеристики измеряются электрическими средствами, т. е. дискретность контроля мала, и результаты можно использовать незамедлительно. Однако стоит задача обработки большого количества информации. В данной работе предлагается использовать нейронные сети для получения значения энергопотребления, обучение которой происходит по методу обратного распространения ошибки. Также проведено сравнение рассматриваемого метода с встроенным методом для построения нейронной сети программного пакета Matlab.
Обучение нейронной сети по методу обратного распространения ошибки. Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.
Прогнозирование с помощью нейронной сети методом обратного распространения ошибки происходило в несколько этапов:
Этап 1. Инициализация и исходные данные. Исходные данные по энергопотреблению имеют значения за период с 01.01.2010 по 31.03.2011. Обучение сети, то есть определение весов и смещений для всех нейронов выполняется на периоде значений с 01.01.2010 по 31.12.2010. В качестве тестового был выбран период с 01.01.2011 по 31.03.2011.
Этап 2. Предварительная обработка исходных данных. Нейронная сеть работает со значениями временных рядов от 0 до 1. Исходные значения энергопотребления в массиве выходят далеко за этот диапазон. Для использования нейронной сети необходимо предварительно нормировать исходный временной ряд, как показано на рис. 1.
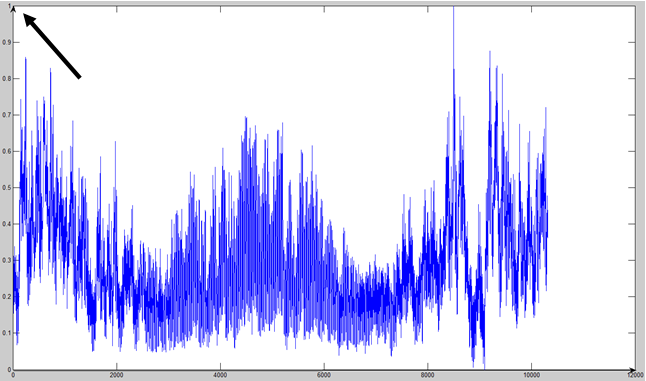
Рис. 1. График нормированных значений энергопотребления
Этап 3. Настройка нейронной сети. Для прогнозирования использовалась трехслойная полносвязная нейронная сеть (рис. 2).
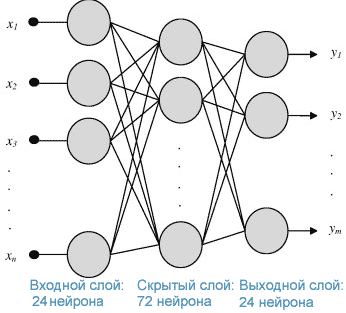
Рис.2. Структура нейронной сети
В результате эксперимента было выявлено, что наилучший результат получается, если на вход нейронной сети подается 24 значения за двое предыдущих суток, скрытый слой после нескольких попыток стал содержать 72 нейрона, а на выходе мы получаем 24 спрогнозированных значений энергопотребления на будущие сутки (рис. 3).
Этап 4. Обучение сети. Двойной цикл по эпохам и внутренней корректировки был взят из примера Хайкина [1]. Такое обучение называется обучением нейронной сети по методу “back propagation error” (обратное распространение ошибки).
Этап 5. Тестовое прогнозирование. На пятом этапе формируется тестовый массив и прогнозируются значения энергопотребления с помощью полученной нейронной сети (рис. 3). При подаче на вход нейронной сети 48 значений энергопотребления график модели и объекта имеют вид, представленный на рис. 3.
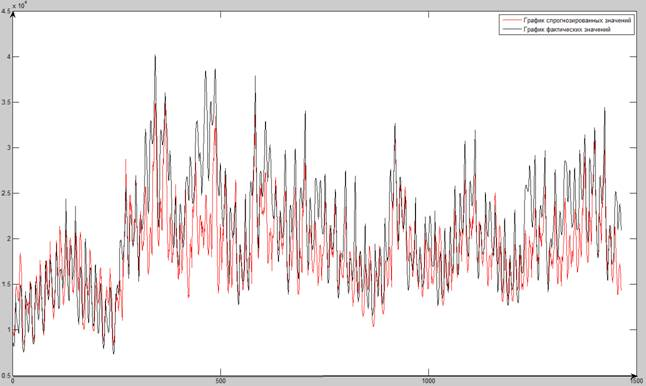
Рис. 3. График фактического и спрогнозированного значения
Количество эпох обучения 600. О качестве полученной модели будем судить по значению средней абсолютной ошибке в процентах (MAPE).
Ошибка прогнозирования MAPE в данном случае получилась равной 13.725 %. Судя по величине ошибки модель адекватно описывает поведение объекта.
На рис. 4 представлен график модели и объекта, при подаче на вход нейронной сети 24 значения энергопотребления, т. е. при прогнозе учитываем предыдущие сутки.
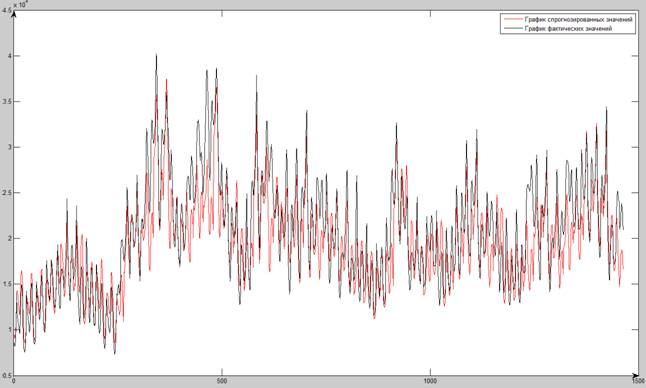
Рис. 4. График фактического и спрогнозированного значения
Количество эпох обучения 600. Величина MAPE оставила около 10.8845 %, что показывает в целом адекватность разработанной нейросетевой модели прогнозирования. Созданная нейронная сеть обучается очень быстро: от 60 до 120 секунд в зависимости от мощности компьютера.
Использование встроенного функционала Matlab для построения нейронной сети. Для реализации нейронно-сетевых концепций разработано большое количество специализированных программных средств. Пакет фирмы «The MathWorks» MATLAB также предоставляет пользователям возможность работы с нейронными сетями. Использование «Neural Network Toolbox» совместно с другими средствами MATLAB открывает широкий простор для эффективного комплексного использования современных математических методов для решения самых разных задач прикладного и научного характера.
Для построения модели прогнозирования энергопотребления был доработан типовой функционал среды Matlab. Обучение сети происходило с помощью алгоритма Левенберга — Маркуардта. Обучающая выборка составляла 80 % от всего объема выборки. Тестовая выборка 20 %. Полный объем выборки равен 10320 значениям энергопотребления на каждый час.
На рис. 5 изображен график прогнозирования энергопотребления методом нелинейной авторегрессии (NAR).
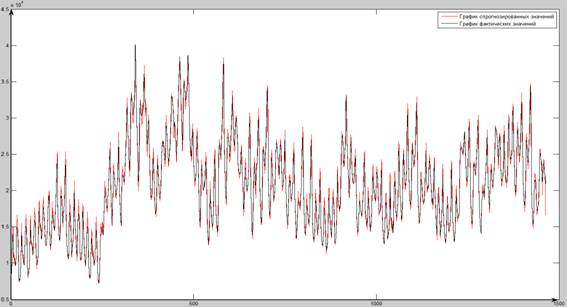
Рис. 5. График модели и объекта
В этом случае на вход подавались значения только энергопотребления. Для прогноза следующего значения энергопотребления использовались ранее спрогнозированные значения.
Величина MAPE составила 3.32652 %, что показывает адекватность разработанной нейросетевой модели прогнозирования. Однако это далеко не предел точности. Предлагается при обучении сети использовать метод нелинейной авторегрессии с расширенным входом. Помимо энергопотребления на вход также подается температура.
Ошибка прогнозирования MAPE, с использованием метода нелинейной авторегрессии с расширенным входом, составила всего 2.46294 %. При таких небольших значениях ошибки разница с предыдущим методом обучения нейронной сети весьма ощутима. При прогнозировании энергопотребления борьба за десятые доли процентов ведется постоянно, так как, например, расходы на покупку электроэнергии напрямую зависят от точности прогноза собственного энергопотребления.
Заключение. Прогнозирование временных рядов энергопотребления показало высокую эффективность реализованных моделей. Значения ошибки прогнозирования MAPE при обучении сети методом обратного распространения ошибки лежит в пределах от 10.8 % до 13 %, что сравнительно хуже значений, полученных при помощи новейших методов обучения нейронной сети.
Литература:
1. Хайкин, С. Нейронные сети: полный курс / С. Хайкин. — М.: ООО «И. Д. Вильямс», 2008. — 1104 с.







