Поставлена математическая задача о конкуренции на линейном ареале двух популяций. Математическая модель представляет собой краевую задачу для системы двух нелинейных дифференциальных уравнений в частных производных. Исследуется устойчивость стационарных состояний. Для построения численного решения предлагается вариационный метод с представлением решений в виде тригонометрических рядов.
Ключевые слова: популяция, краевые задачи, математическое моделирование.
Введение. Математическому моделированию конкуренции двух взаимодействующих популяций посвящено большое число работ [1, 2, 6, 8, 18, 19, 25, 26, 36, 37, 40, 51, 52, 56, 57, 60–63, 66–67]. В основе математических моделей лежит задача Коши для системы обыкновенных дифференциальных уравнений. Распространение особей в пространстве в таких моделях не учитывается. Реальные популяции живут на ограниченных территориях с различными свойствами среды обитания в разных ее частях [4, 5, 11, 15, 35, 45, 64]. Часть особей по различным причинам (например, в поисках пищи или свободных мест обитания) склонна к перемещению по территории. Как показывает анализ результатов полевых наблюдений [4, 35, 45, 64] перемещение особей происходит случайным образом. В моделях с распределенными параметрами, в которых учитывается пространственное распределение особей популяции, вводится плотность популяции на единицу длины, площади или объема, и считается, что особи распределены в пространстве [3–5, 12, 18, 30–34, 49, 56, 64]. Среда обитания считается сплошной, что позволяет использовать аппарат дифференциальных уравнений в частных производных, широко применяемый при разработке математических моделей сплошных сред с нелинейными свойствами [16, 20, 27–29, 41–44, 53–55, 58, 59, 65].
Существенное влияние на биоценозы оказывает и производственная деятельность человека, приводящая к изменению условий существования флоры и фауны. Для учета негативных последствий, вносимых человеком нарушений в ход эволюционных процессов, в модели популяционной биологии необходимо подключать модели математической экономики [13, 14, 38, 39, 47].
Задача анализ результатов полевых наблюдений является отдельной и достаточно сложной задачей. Здесь не просто выявить основные причины, характеризующие конкуренцию и, соответственно, определить значения параметров необходимых для разработки математических моделей [17, 21–24, 48].
Математическая модель конкуренции. Для описания динамики численности двух конкурирующих популяций Вольтера, Лотка и Гаузе [2, 4, 64] была предложена математическая модель
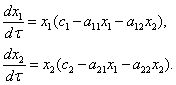 (1)
(1)
В этих уравнениях 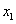 и
и 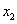 — численности двух конкурирующих видов,
— численности двух конкурирующих видов, 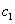 ,
, 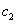 ,
, 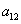 ,
, 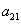 ,
, 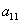 и
и 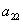 — постоянные (положительные) коэффициенты,
— постоянные (положительные) коэффициенты, 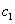 и
и 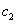 — удельные скорости роста популяций при их малой численности,
— удельные скорости роста популяций при их малой численности, 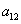 и
и 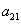 — коэффициенты межвидовой конкуренции,
— коэффициенты межвидовой конкуренции, 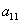 и
и 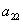 — коэффициенты внутривидовой конкуренции [2].
— коэффициенты внутривидовой конкуренции [2].
Система уравнений (1) заменой [2]
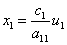 и
и 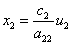
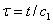
приводятся к виду
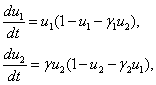 (2)
(2)
где 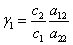 ,
, 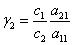 ,
, 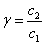 .
.
Система уравнений (2) имеет четыре стационарные точки
1. 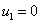 ,
, 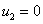 .
.
2. 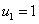 ,
, 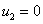 .
.
3. 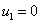 ,
, 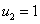 .
.
4. 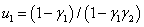 ,
, 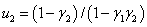 , если
, если 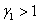 и
и 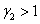 или
или 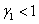 и
и 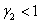 .
.
Стационарные точки системы уравнений (2) считаются устойчивыми, если все собственные значения матрицы Якоби
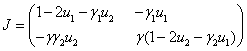
правой части уравнения (2) в этих точках имеют отрицательные вещественные части [7].
Первая стационарная точка неустойчива, поскольку оба собственных значения якобиана 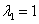 и
и 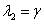 положительны. То есть в рассматриваемой модели из двух малочисленных конкурирующих популяций хотя бы одна выживет.
положительны. То есть в рассматриваемой модели из двух малочисленных конкурирующих популяций хотя бы одна выживет.
Во второй стационарной точке собственные значениями матрицы Якоби 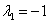 и
и 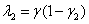 будут отрицательными, если выполнится неравенство
будут отрицательными, если выполнится неравенство 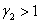 . В этом случае стационарная точка будет устойчивой, а при выполнении неравенства
. В этом случае стационарная точка будет устойчивой, а при выполнении неравенства 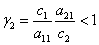 — неустойчивой. То есть выживаемость первой популяции (условие
— неустойчивой. То есть выживаемость первой популяции (условие 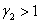 ) в условиях конкуренции обеспечивается большей скоростью роста ее численности по сравнению со скоростью роста численности второй популяции (
) в условиях конкуренции обеспечивается большей скоростью роста ее численности по сравнению со скоростью роста численности второй популяции (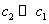 ) и низкой внутривидовой конкуренцией по сравнению с межвидовой (
) и низкой внутривидовой конкуренцией по сравнению с межвидовой (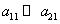 ). Аналогичный результат следует и для третьей стационарной точки, в которой
). Аналогичный результат следует и для третьей стационарной точки, в которой 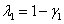 и
и 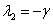 . Эта точка устойчива, если
. Эта точка устойчива, если 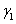 >1 и неустойчива, если
>1 и неустойчива, если 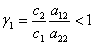 .
.
В четвёртой стационарной точке характеристическое уравнение
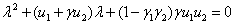
имеет корни с отрицательными вещественными частями, если 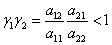 , и корни противоположных знаков, если
, и корни противоположных знаков, если 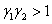 . То есть эта стационарна точки будет устойчивой, если внутривидовая конференция оказывает большее влияние на численность популяции, чем межвидовая (
. То есть эта стационарна точки будет устойчивой, если внутривидовая конференция оказывает большее влияние на численность популяции, чем межвидовая (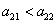 ,
, 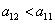 ). При этом в четвертой стационарной точке, если она устойчивая,
). При этом в четвертой стационарной точке, если она устойчивая, 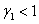 и
и 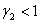 .
.
Таким образом, в системе конкурирующих видов побеждает тот, кто сильнее подавляет конкурента: 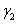 >1 или
>1 или 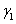 >1. При выполнении одного из этих неравенств четвертая стационарная точка либо не имеет физического смысла, либо будет неустойчивой. Поэтому один из видов исчезает. Если внутривидовая конкуренция слабее межвидовой (
>1. При выполнении одного из этих неравенств четвертая стационарная точка либо не имеет физического смысла, либо будет неустойчивой. Поэтому один из видов исчезает. Если внутривидовая конкуренция слабее межвидовой (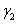 <1 и
<1 и 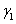 <1), то совместное существование популяций будет устойчивым.
<1), то совместное существование популяций будет устойчивым.
Модель конкуренции на линейном ареале. Примерами линейных ареалов служат трубопроводы, обочины дорог, лесные просеки [4, 11, 15, 35, 45, 64]. Математическая модель конкуренции двух видов (2) на отрезке представляется системой двух эволюционных уравнений [18, 19, 33, 49, 56, 64]
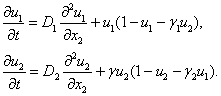 (3)
(3)
В этих уравнениях 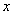 — координата,
— координата, 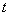 — время,
— время, 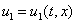 и
и 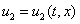 — линейные плотности популяций,
— линейные плотности популяций, 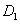 и
и 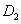 — параметры, характеризующие подвижности особей.
— параметры, характеризующие подвижности особей.
В качестве начальных условий задается значение функций 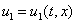 и
и 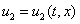 в начальный момент времени: при
в начальный момент времени: при 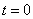
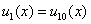 ,
, 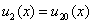 .
.
В качестве граничных условий для случая отрезка длиной 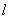 рассматриваются два варианта:
рассматриваются два варианта:
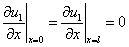 ,
, 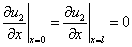 (4)
(4)
и
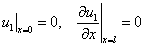 ,
, 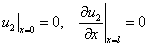 . (5)
. (5)
Условие обращения в ноль функций 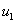 и
и 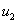 на границе отрезка соответствует невозможности существования популяции в этой точке, а условие обращения в ноль производных
на границе отрезка соответствует невозможности существования популяции в этой точке, а условие обращения в ноль производных 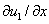 и
и 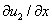 (условие наполнения среды [12, 56, 64]) допускает свободный рост численности популяций.
(условие наполнения среды [12, 56, 64]) допускает свободный рост численности популяций.
Общие численности популяций (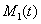 ) и (
) и (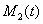 ) на отрезке в момент времени
) на отрезке в момент времени 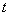 подсчитываются по формулам
подсчитываются по формулам
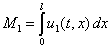 ,
, 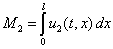 .
.
Устойчивость тривиального решения. Системе уравнений (3) при граничных условиях (4) удовлетворяют функции, не зависящие от пространственной координаты. Потому устойчивость решений уравнений (3) при граничных условиях (4) будет совпадать и с устойчивостью решений уравнений (2). Поэтому ниже будет исследоваться устойчивость решений, удовлетворяющих только граничным условиям (5).
В стационарном случае системе уравнений (3) при граничных условиях (5) удовлетворяет тривиальное решение 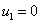 ,
, 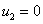 . Возмущение этого равновесного состояния представляется в виде [9, 10, 56, 59]
. Возмущение этого равновесного состояния представляется в виде [9, 10, 56, 59] 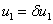 ,
, 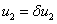 , где
, где 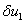 и
и 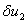 малые по сравнению с единицей величины:
малые по сравнению с единицей величины: 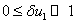 ,
, 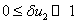 . Тогда уравнения (3) с точностью до величин второго порядка малости [27, 56, 58] приводятся к виду
. Тогда уравнения (3) с точностью до величин второго порядка малости [27, 56, 58] приводятся к виду
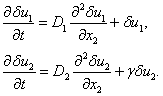
Решение этих уравнений, удовлетворяющее граничным условиям (5), представляется в виде тригонометрических рядов
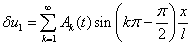 ,
, 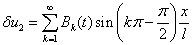 .
.
При этом коэффициенты разложения должны удовлетворять уравнениям
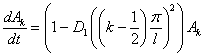 ,
, 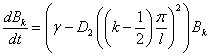 (
(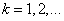 .).
.).
Отсюда следует, что при выполнении неравенства 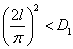 все коэффициенты
все коэффициенты 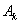 будут убывающими функциями времени и, соответственно, решение
будут убывающими функциями времени и, соответственно, решение 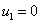 будет устойчивым. А при выполнении неравенства
будет устойчивым. А при выполнении неравенства 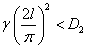 будет устойчивым решение
будет устойчивым решение 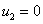 . Последнее означает, что при высокой подвижности особей малочисленные популяции в рассматриваемой модели погибают. Аналогичный результат получен в [12] для одиночной популяции.
. Последнее означает, что при высокой подвижности особей малочисленные популяции в рассматриваемой модели погибают. Аналогичный результат получен в [12] для одиночной популяции.
Численное решение. Построить аналитическое решение нелинейных уравнений (3) не представляется возможным. Поэтому используются различные методы аппроксимаций уравнений (3) или их решений. Наибольшее распространение получили конечно-разностная аппроксимация уравнений и вариационные методы, основанные на представлении решения в виде линейной комбинации аналитических функций [46, 50, 58]. Численное решение уравнений (3), удовлетворяющее граничным условиям (5) на отрезке ищется в виде суммы тригонометрических функций [56, 58]
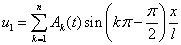 ,
, 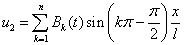 . (6)
. (6)
Система функций 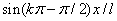 (
(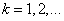 ) удовлетворяет граничным условиям (5), является полной и ортогональной [58] на отрезке
) удовлетворяет граничным условиям (5), является полной и ортогональной [58] на отрезке 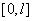 . После подстановки выражений (6) в уравнения (3), умножения последних на
. После подстановки выражений (6) в уравнения (3), умножения последних на 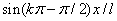 (
(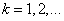 ) и последующего интегрирования по промежутку
) и последующего интегрирования по промежутку 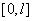 будет получена система обыкновенных дифференциальных уравнений для коэффициентов
будет получена система обыкновенных дифференциальных уравнений для коэффициентов 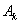 и
и 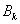 (
(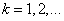 )
)
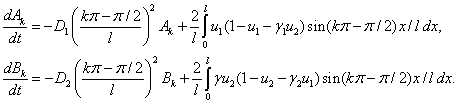 (7)
(7)
Начальные условия для функций 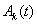 и
и 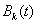 (
(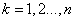 ) определяются из соотношений
) определяются из соотношений
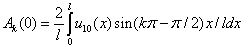 ,
,
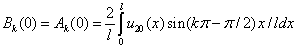 .
.
Для одного члена разложения (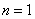 ) в (6) для случая отрезка единичной длины (
) в (6) для случая отрезка единичной длины (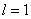 ) коэффициенты
) коэффициенты 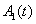 и
и 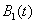 удовлетворяют уравнениям
удовлетворяют уравнениям
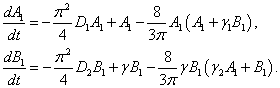 (8)
(8)
Матрица Якоби правой части этих уравнений
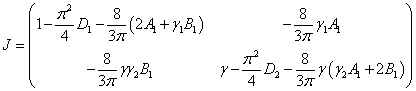 .
.
Система уравнений (8) имеет четыре стационарные точки.
1. 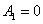 ,
, 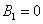 .
.
В этой стационарной точке собственные значения
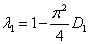 и
и 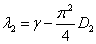
матрицы Якоби будут отрицательными, если выполняются неравенства 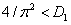 и
и 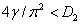 . В этом случае тривиальная стационарная точка будет устойчивой. То есть при высокой подвижности особей обе популяции могут погибнуть.
. В этом случае тривиальная стационарная точка будет устойчивой. То есть при высокой подвижности особей обе популяции могут погибнуть.
2. Во второй стационарной точке
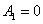 ,
, 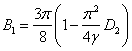 .
.
Эта стационарная точка будет устойчивой, если собственные значения матрицы Якоби
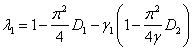 ,
, 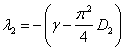
будут отрицательными.
3. В третьей стационарной точке
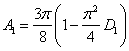 ,
, 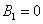
Эта стационарная точка будет устойчивой, если собственные значения матрицы Якоби
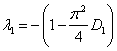
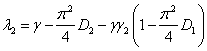
будут отрицательными.
4. В четвертой стационарной точке
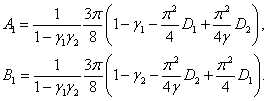 (9)
(9)
При выполнении неравенства 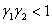 при положительных значениях
при положительных значениях 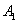 и
и 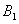 вторая и третья стационарные точки будут неустойчивыми.
вторая и третья стационарные точки будут неустойчивыми.
Собственные значения матрицы Якоби в рассматриваемой стационарной точке являются корнями квадратного уравнения
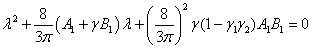 .
.
Корни этого уравнения при выполнении неравенств 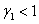 и
и 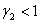 будут иметь отрицательные вещественные части. То есть эта стационарная точки будет устойчивой, если
будут иметь отрицательные вещественные части. То есть эта стационарная точки будет устойчивой, если 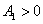 и
и 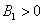 . При этом вторая и третья стационарные точки будут неустойчивыми.
. При этом вторая и третья стационарные точки будут неустойчивыми.
Общая численность популяции на отрезке подсчитывается по формулам 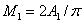 и
и 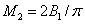 . И как следует из (9) увеличение подвижности одной популяции (параметров
. И как следует из (9) увеличение подвижности одной популяции (параметров 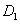 или
или 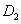 ) приводит к уменьшению ее общей численности на отрезке и увеличению общей численности конкурирующей популяции.
) приводит к уменьшению ее общей численности на отрезке и увеличению общей численности конкурирующей популяции.
Таким образом, условия существования четвертой стационарной точки при условии, что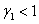 и
и 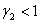 , определяются системой неравенств
, определяются системой неравенств
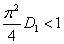 ,
, 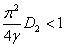 ,
, 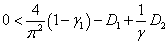 ,
, 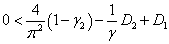 .
.
В системе координат 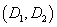 эти неравенства определяют область значений параметров
эти неравенства определяют область значений параметров 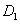 и
и 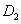 , в которой четвертая стационарная точка реализуется и является устойчивой (рис. 1,
, в которой четвертая стационарная точка реализуется и является устойчивой (рис. 1, 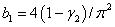 ,
, 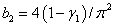 )
)
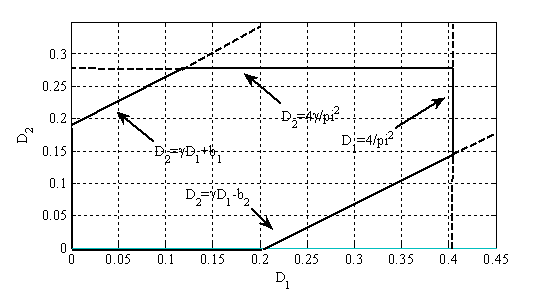
Рис. 1. Границы области устойчивости нетривиального стационарного решения (9) в системе координат (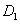 ,
,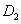 )
)
Анализ поведения решения при большем числе слагаемых в представлениях (6) не представляется возможным без использования численных методов. Решение задачи Коши для системы уравнений (7) осуществлялось с применением численных методов типа Рунге-Кутты [46]. Некоторые из результатов численных экспериментов приведены на рис. 2–4 (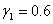 ,
, 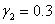 ,
, 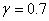 ).
).
На рис. 2 показано изменение коэффициентов 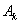
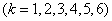 как «функции»
как «функции» 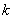 в установившемся режиме (
в установившемся режиме (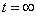 ) для случая
) для случая 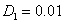 ,
,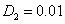 , а на рис. 3 —
, а на рис. 3 — 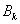 . Как следует из рис. 2 и рис. 3 при решении нелинейных уравнений с высокой степенью точности можно ограничиться 2–3 членами в представлениях (6).
. Как следует из рис. 2 и рис. 3 при решении нелинейных уравнений с высокой степенью точности можно ограничиться 2–3 членами в представлениях (6).
На рис. 4 отражено изменение функций 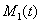 и
и 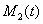 (общей численности популяций на отрезке) в зависимости от значений параметров
(общей численности популяций на отрезке) в зависимости от значений параметров 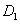 и
и 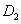 . Пара кривых
. Пара кривых 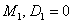 (первая популяция) и
(первая популяция) и 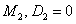 (вторая популяция) соответствуют решению системы уравнений (2), а пара кривых
(вторая популяция) соответствуют решению системы уравнений (2), а пара кривых 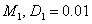 и
и 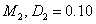 — системе уравнений (7). Как следует из этого рисунка высокая подвижность особей приводит к уменьшению общей численности популяции.
— системе уравнений (7). Как следует из этого рисунка высокая подвижность особей приводит к уменьшению общей численности популяции.
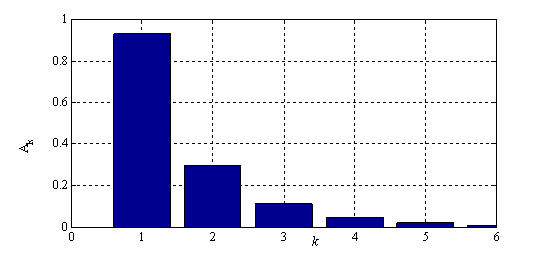
Рис. 2. Значения коэффициентов 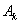
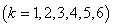 в (6) при
в (6) при 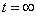
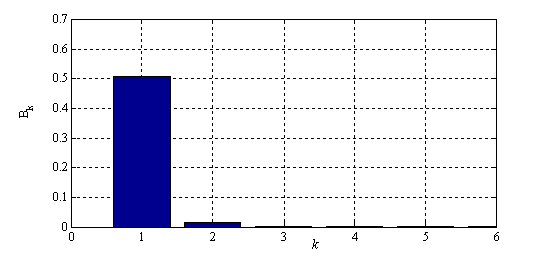
Рис. 3. Значения коэффициентов 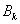
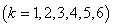 в (6) при
в (6) при 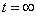
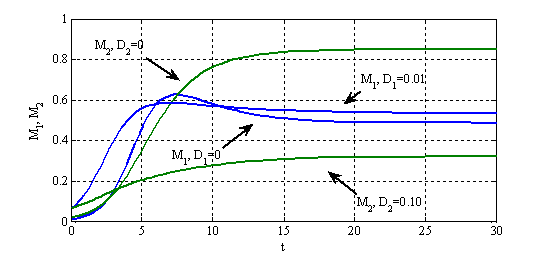
Рис. 4. Изменение функций 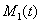 и
и 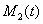 (общей численности популяций на отрезке) в зависимости от значений параметров
(общей численности популяций на отрезке) в зависимости от значений параметров 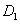 и
и 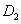
Заключение. Учет неоднородности среды обитания в математических моделях двух конкурирующих популяций приводит к результатам, не содержащихся в точечных моделях. С ростом подвижности особей уменьшается общая численность популяции. При этом численность конкурирующей популяции увеличивается. Существует критическая подвижность особей, превышение которой приводит к гибели популяции.
Литература:
- Апонин Ю. М., Апонина Е. А. Принцип инвариантности Ла-Салля и математические модели эволюции микробных популяций // Компьютерные исследования и моделирование. — 2011. — Т. 3. — № 2. — С. 177–190.
- Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий. — 2003. 368 с.
- Балыкина Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.
- Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в двух томах. М.: Мир, 1989. Т. 1. 667 с. Т. 2. 477с.
- Будянский А. В., Цибулин В. Г. Моделирование пространственно-временной миграции близкородственных популяций // Компьютерные исследования и моделирование. — 2011. — Т. 3. — № 4. — С. 477–488.
- Викторов А. А., Холоднов В. А., Гладких В. Д., Алехнович А. В. Математическая модель влияния окружающей среды на старение живых систем // Успехи геронтологии. — 2013. — Т. 26. — № 1. — С. 52–57.
7. Виташевская И. С., Олемской И. В., Хитров Г.М О некоторых инвариантах квадратных (од)-матриц // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2007. — № 1. — С. 38–45.
- Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий. — 2004. — 288 с.
- Гасратова Н. А. Напряженно-деформированное состояние упругого пространства со сферическим жестким включением // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 1. — С. 14–18.
- Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 2. — С. 122–128.
- Гилев А. В. Закономерности пространственного распределения и научные основы охраны рыжих лесных муравьев // Зоологический журнал. — 2010. — Т. 89. — № 12. — С. 1413–1420.
- Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вест. С.-Петерб. ун-та. Сер. 10. — 2012. — Вып. 4. — С. 18–30.
13. Григорьева К. В., Иванов А. С., Малафеев О. А Статическая коалиционная модель инвестирования инновационных проектов // Экономическое возрождение России. — 2011. — № 4. — С. 90–98.
- Григорьева К. В., Малафеев О. А. Динамический процесс кооперативного взаимодействия в многокритериальной (многоагентной) задаче почтальона // Вестник гражданских инженеров. — 2011 — № 1. — С. 150–156.
- Громов В. С. Пространственно-этологическая структура популяций грызунов. М.: Т-во научн. изданий КМК. 2008. 581 с.
- Даль Ю. М., Пронина Ю. Г. Деформация шаровой поры в нелинейно-упругом теле // Известия Российской академии наук. Серия физическая. — 2006. — Т. 70. — № 9. — С. 1341–1343.
17. Жабко Н. А. Параметрическая идентификация динамических моделей морских судов // Вестник Воронежского государственного технического университета. — 2012. — Т. 8. — № 1. — С. 80–84.
- Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
- Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
- Кабриц С. А. Мальков В. М., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.
- Карелин В. В Один подход к задаче оценки параметров динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 31–36.
- Карелин В. В Точные штрафы в задаче наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2008. — № 4. — С. 3–8.
- Карелин В. В. Точные штрафы в задаче оценки координат динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 4. — С. 40–46.
- Карелин В. В. Штрафные функции в задаче управления процессом наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2010. — № 4. — С. 109–114.
- Колобов А. Н. Численно-аналитическое исследование модели роста дерева в условиях конкуренции за свет // Математическая биология и биоинформатика. — 2012. — Т. 7. — № 1. — С. 125–138
- Колокольцов В. Н., Малафеев О. А. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть I) // Вестник гражданских инженеров. — 2010 — № 4 — С. 144–153.
- Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
- Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
- Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2(61). — С. 19–24.
- Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28–33.
- Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
- Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
- Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
- Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
- Коробченко М. А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. — 2009. — Т. 88. — № 4. — С. 465–472.
36. Лежнина Е.А Свойство подтверждения и аксиоматизация наименьшего ядра // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2010. — № 1. — С. 50–64.
- Лугин В. Г. Математическое моделирование распространения новшеств с использованием стохастической фрактальной клеточной модели // Международный журнал прикладных и фундаментальных исследований. — 2014. — № 4. — С. 109–114.
- Малафеев О. А., Пахар О. В. Динамическая нестационарная задача инвестирования проектов в условиях конкуренции // Проблемы механики и управления: Нелинейные динамические системы. — 2009. — № 41. — С. 103–108.
39. Малафеев О. А., Соснина В. В. Модель управления процессом кооперативного трехагентного взаимодействия // Проблемы механики и управления: Нелинейные динамические системы. — 2007. — № 39. — С. 131–144.
- Малков С. Ю., Кирилюк И. Л. Моделирование динамики конкурирующих сообществ: варианты взаимодействия // Информационные войны. — 2013. — № 2 (26). — С. 49–56.
- Мальков В. М., Малькова Ю. В. Исследование нелинейной задачи Фламана // Известия Российской академии наук. Механика твердого тела. — 2006. — № 5. — С. 68–78.
- Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для несжимаемого материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 4. — С. 73–82.
- Мальков В. М., Малькова Ю. В., Иванов В. А. Бесконечная плоскость с круговым включением, имеющим отслоение на части границы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 152–165.
- Мальков В. М., Малькова Ю. В.Плоская задача нелинейной упругости для гармонического материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 3. — С. 114–126.
- Мамонтов С. Н. Распределение по стволу дерева короеда-типографа (ips typographus, coleoptera, scolyniddae) и его энтомогафов // Зоологический журнал. — 2009. — Т. 88. — № 9. — С. 1139–1145.
- Матросов А. В. Сходимость степенных рядов в методе начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 1. — С. 41–51.
- Миндлин Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
48. Мышков С. К., Полякова Л. Н., Тарасова В. В. О применимости численных методов негладкого анализа к решению линейной квадратичной задачи оптимального управления с неполной информацией [6]) // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2005. — № 3–4. — С. 130–137.
- Мятлев В. Д., Панченко Л. А., Ризниченко Г. Ю., Терехин А. Т. Теория вероятностей и математическая статистика. Математические модели. М.: Издательский центр «Акадкмия», 2009. 320 с.
- Олемской И. В. Модификация алгоритма выделения структурных особенностей // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 2. — С. 55–64.
- Орлова Е. В., Ульмасова И. С. Методы ценообразования и их использование на высоко конкурентном рынке // Молодой ученый. — 2014. — № 3 (62). — С. 495–497.
- Поспелов И. Г., Радионов С. А. Динамика количества фирм в рамках концепции экономики разнообразия // Математическое моделирование. — 2014. — Т. 26. — № 2. — С. 65–80.
- Пронина Ю. Г. Периодическая задача о точечных воздействиях в упругой полуплоскости с отверстиями // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 3. — С. 118–128.
- Пронина Ю. Г. Сосредоточенные силы и моменты в упругой полуплоскости с отверстием // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 2. — С. 104–114.
- Пронина Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.
- Ризниченко Г. Ю., Рубин А. Б. Биофизическая динамика продукционных процессов. Москва — Ижевск: Институт компьютерных технологий, 2004. — 464 с.
- Садыков О. Ф., Бененсон И. Е. Динамика численности мелких млекопитающих: Концепции, гипотезы, модели. М.: Наука, 1992. 191 с.
- Тихонов А. Н., Самарский А. А. Уравнение математической физики. М.: Наука, 1972. 735 с.
- Черных К. Ф., Кабриц С. А., Колпак Е. П., Слепнева Л. В. Точные решения краевых задач нелинейной теории упругости // отчет о НИР № 96–01–00739 (Российский фонд фундаментальных исследований).
- Шестакова Т. П. Исследование одной математической модели конкуренции трех популяций // Инновации в науке. — 2012. — № 7. — С. 6–11.
- Braselton J., Waltman P. A competition model with dynamically allocated inhibitor production // Mathematical Biosciences. — 2001. V. 173. — N 2. — P. 55–84.
- Křivan V. Competition in di- and tri-trophic food web modules // Journal of Theoretical Biology. — 2014. — V. 343. — P. 127–137.
63. Mirrahimi S., Perthame B., Yuichiro Wakano J. Direct competition results from strong competition for limited resource // Journal of Mathematical Biology. — 2014. — V. 68. — 931–949.
- Murray D. D. Mathematical biology. N. Y. Springer. 2002. — 551 p.
- Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — С. 361–364
66. Sanling Yuan, Dongmei Xiao, Maoan Han Competition between plasmid-bearing and plasmid-free organisms in a chemostat with nutrient recycling and an inhibitor // Mathematical Biosciences. — 2006. — V. 202. — N 1. — P. 1–28.
67. Sze-Bi Hsu, Xiao-Qiang Zhao A Lotka–Volterra competition model with seasonal succession // Journal of Mathematical Biology. — 2012. — DOI 10.1007/s00285–011–0408–6.







