Прогнозирование денежных потоков инвестиционного проекта

В период резких изменений в экономике, технологии, экологии и политики выживание и успех в мире бизнеса, в большей степени, чем когда-либо зависят от правильности принимаемых инвестиционных решений. Инвестиционное решение — одна из наиболее важных деловых инициатив, которая должна осуществляться предпринимателями или менеджерами, поскольку инвестиции связывают финансовые ресурсы на относительно большой период времени. Инвестиционное решение воплощается в инвестиционный проект. Центральное место в комплексе мероприятий по определению степени обоснованности инвестиционных решений и анализу эффективности инвестиционных проектов занимает оценка будущих денежных потоков, возникающих в результате вложения средств.

Прогнозирование денежных потоков — одна из наиболее важных и в то же время наиболее трудоемких задач для специалистов по разработке инвестиционных проектов. Подготовка исходной информации для составления такого прогноза ведется целой командой специалистов, в которую входят специалисты по исследованию рынков, инженеры, экономисты, занимающиеся проблемами себестоимости, сотрудники отделов кадров, финансисты, экологи и т. д. Очевидно, что на основе полученных результатов определяются и все остальные параметры производственно-финансовой деятельности фирмы.

Наиболее важным элементом всех прогнозов является прогноз продаж. Достоверность этого показателя особенно важна, так как обоснование инвестиционного проекта основывается именно на этом элементе. На сегодняшний день наука достаточно далеко продвинулась в разработке технологий прогнозирования. К ним относят анализ временных рядов, метод скользящих средних, анализ безубыточности, факторный анализ, дерево решений, использование экономических моделей, экспертные оценки и т. д.

Покажем на примере применение метода корреляционно-регрессионного анализа для расчета будущего объема продаж. Для экономического прогнозирования разработано множество соответствующих программных пакетов, но они, к сожалению, не всегда доступны. Однако, многие из этих проблем можно достаточно успешно решать в широко известном и распространенном пакете прикладных программ MS Excel.

План продаж — это прогноз поступлений денежных средств компании в оплату за товары, работы, услуги. Качество составления плана продаж очень важно, так как без четкого прогноза доходов компании невозможно определить ключевые финансовые показатели, а следовательно, принять решение о разработке стратегии и тактики на прогнозный период. В планах должны стоять конкретные цифры, которые лучше брать не с потолка, а вычислять с помощью моделей. Покажем, как для прогнозирования плана продаж может быть применен регрессионный анализ, позволяющий строить модели на основе взаимодействия признаков. В качестве наглядного примера приведем зависимость между интенсивностью вложений в рекламную деятельность и объемами продаж одной из фирм. Исходные данные для расчета будущего объема продаж приведены в Таблице 1 [1].

Таблица 1

Исходные данные для расчета будущего объема продаж

В простейшем случае регрессия для объема продаж (Q) и одной независимой переменной (X) может быть представлена следующим уравнением:

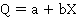
Использование метода наименьших квадратов позволяет аналитику определить такие величины a и b, чтобы полученные из уравнения регрессии значения показателя Q как можно меньше отличались от наблюдаемых его значений. Однако в практике финансового анализа для нахождения a и b в уравнении линейной регрессии с одной независимой переменной применяют упрощенный подход, в рамках которого рассчитываются искомые коэффициенты по следующим формулам:

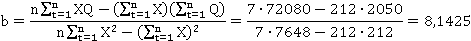
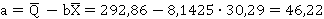
где n — число наблюдений, 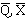 — средние арифметические объема продаж и затрат на рекламу соответственно.

После того как были получены значения a и b, уравнение регрессии для рассматриваемого примера будет представлено выражением

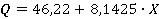
Иллюстрация решения рассматриваемой задачи с использованием MS Excel приведена на Рисунке 1.

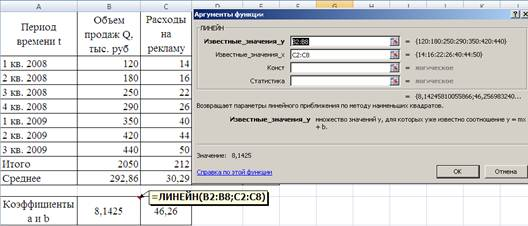
Рис. 1. Фрагмент окна MS Excel c функцией ЛИНЕЙН

Если финансовые аналитики в следующем квартале планируют произвести затраты на рекламную деятельность на сумму 100 тыс. руб., то прогнозируемый объем продаж составит, тыс. руб.:

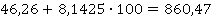
При желании достичь объема продаж в размере 1000 тыс. руб. финансистам следует планировать расходы на рекламную деятельность 117,14 тыс. руб.:

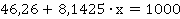
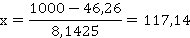
Следующим шагом в рассматриваемом примере будет проверка адекватности регрессионной модели. Чтобы определить, насколько построенное уравнение регрессии подходит для конкретного случая, рассчитаем такие показатели качества и надежности регрессионного анализа, как среднюю ошибку аппроксимации, коэффициент детерминации и среднюю ошибку предвидения. Исходные данные для проверки адекватности регрессионной модели приведены в Таблице 2.

Таблица 2

Исходные данные для проверки адекватности регрессионной модели

Чтобы иметь общее суждение о качестве построенной модели, определим среднюю ошибку аппроксимации, которая показывает среднее отклонение расчетных данных от фактических.

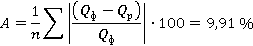
где Q_ф — фактический объем продаж, тыс. руб.;

Q_р — рассчитанный объем продаж с помощью уравнения регрессии;

n — число наблюдений (n=7).

Чем меньше средняя ошибка аппроксимации (A), тем ближе Q_р к Q_ф. Практически полагают, что значение средней ошибки аппроксимации не должно превышать 12–15 % для грубого приближения регрессии к реальной зависимости.

Коэффициент детерминации (D) позволяет определить качество регрессионной модели, назначение которого состоит в оценке тесноты связи между результативной (Q) и факторной переменной (X). Коэффициент детерминации равен D = r² = 0,9753² = 0,9513. Коэффициент детерминации изменяется в пределах между 0 и 1. Чем ближе D к единице, тем точнее выбрана функция, описывающая зависимость между результативной переменной и факторной переменной.

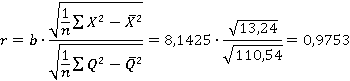
где n — число наблюдений, 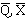 — средние арифметические объема продаж и затрат на рекламу соответственно, b — коэффициент регрессии.

Таким образом, около D=95,13 % изменений в объеме продаж происходит в зависимости от величины средств, израсходованных на рекламу, остальные 4,86 % происходят под влиянием прочих не учтенных в процессе анализа факторов.

Чтобы перейти от относительных величин к стоимостным показателям при измерении точности прогнозирования, на практике рассматривается еще один показатель — средняя ошибка предвидения S_e. В нашем примере расчета будущего объема продаж стандартная ошибка оценки прогноза для фирмы составит 28,86 тыс. руб [2], [3].

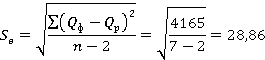
Проверка адекватности регрессионной модели показала, что построенное уравнение регрессии достаточно точно описывает зависимость между интенсивностью вложений в рекламную деятельность и объемами продаж, вычисленные коэффициенты регрессии значимы, и такая модель может быть использована для принятия решений и осуществления прогнозов, в частности денежных потоков инвестиционного проекта.

Литература:

1.         Киселева, О.В., Инвестиционный анализ: учебное пособие / О. В. Киселева, Ф. С. Макеева. — М.:КНОРУС, 2010.-208 с.

2.    Айвазян, С. А. Эконометрика / С. А. Айвазян, С. С. Иванова. — М.:Маркет ДС, 2010. — 104 с.

3.    Елисеева, И. И. Практикум по эконометрике: Учебное пособие. — М.: Финансы и статистика, 2008.-192 с.