Дается качественный анализ математической модели хищник-жертва Базыкина-Свирежева, представляющую собой задачу Коши для системы двух обыкновенных дифференциальных уравнений. Проводится анализ устойчивости стационарных точек в зависимости от параметров, входящих в уравнения.
Ключевые слова: популяция, дифференциальные уравнения, математическое моделирование.
Математическая модель «хищник-жертва» достаточно часто встречается в научных публикациях [1, 2, 5, 6, 16, 26, 28, 29, 32–37, 40]. В основе большинства моделей лежит модель Лотка и Вольтерра, представляющая собой задачу Коши для системы обыкновенных дифференциальных уравнений. Модель объясняет периодическое изменение численности популяций, происходящее в природе. Колебания численности связаны с внешними воздействиями и внутренними изменения в биоценозе. От них зависят период и амплитуда колебаний, механизмы регуляции численности популяций. Однако, эта модель не лучшим образом согласуется с данными полевых наблюдений [4, 18, 20, 23, 25, 30]: амплитуда и период колебаний численности популяций не являются неизменными, на отдельных длительных временных промежутках численность популяций становится минимальной, периодически возникают «вспышки» численности.
Математическая модель, описывающая динамику численности двух популяций, взаимодействующих по принципу хищник-жертва, была предложена Лотка и Вольтерра [2, 6]:
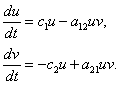(1)
В этих уравнениях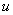 
и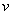 
— численности популяций жертвы и хищника соответственно, 
, 
,
, 
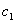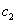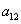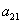— константы. Стационарной точкой системы уравнений (1) является 
, 
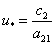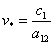. В окрестности этой стационарной точки (центр) происходят гармонические колебания численности обеих популяций с частотой 
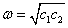[2, 16]. При этом независимо от значений, которые принимают константы, стационарная точка остается центром.
Модель Базыкина-Свирежева [2, 22] представлена системой дифференциальных уравнени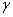й (
и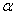 
— константы)
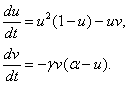(2)
В этой модели учтена внутривидовая конкуренция у жертвы и нелинейность размножения жертвы при малой ее численности.
Система уравнений (2) имеет две нетривиальные стационарные точки:
1. 
, 
.
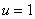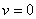2. 
, 
.
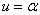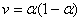В первой стационарной точке собственными значения матрицы Якоби будут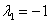 
и 
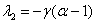. При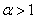 
эта стационарна точка будет устойчивой и, соответственно, хищник «погибает», периодические колебания не возникают.
Во второй стационарной точке, а она имеет физический смысл, если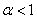 
, собственные значения матрицы Якоби являются корнями квадратного уравнения
.
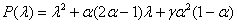При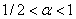 
полином 
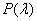в зависимости от значений параметра 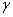будет иметь либо пару комплексно сопряженных корней с отрицательной вещественной частью, либо отрицательные корни. Соответственно, положение равновесия будет устойчивым.
При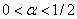 
полином 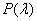будет иметь корни с положительной вещественной часть. В этом случае положение равновесия будет неустойчивым. При 
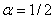стационарная точка является центром.
Третья стационарна точки — тривиальная: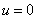 
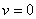, . Одно из собственных значений в этой точке равно нулю. В окрестности этой точки уравнения (2) в линейном приближении принимают вид
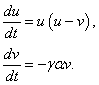
Если на решениях уравнений (1) в окрестности этой стационарной точки будет выполняться неравенство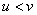 
, то функци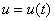и 
и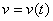 
будут убывающими функциями, стремящимися в точку 
.
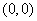Таким образом, при выполнении неравенств 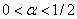все три стационарные точки могут быть неустойчивыми (в зависимости от значения параметра 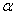). При 
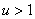производная 
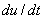отрицательна. Потому 
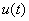не может возрастать до бесконечности и, начиная с какого-то момента времени, станет убывать. Поэтому колебания в рассматриваемой модели могут возникнуть только при выполнении неравенства 
.
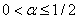Некоторые из результатов численных экспериментов представлены на рис. 1 — рис. 3 (
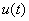). На рис. 1 приведены зависимости функций и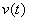 
от времени пр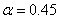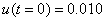и 
, 
и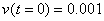 
. На рис. 2 — аналогичные зависимости при 
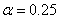, а на рис. 3 — при 
, и значениях 
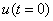и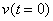 
близких к значениям этих функций во второй стационарной точке (, ).
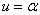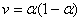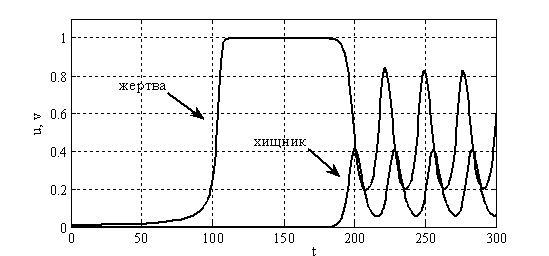
Рис. 1. Изменение функций и от времени при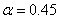
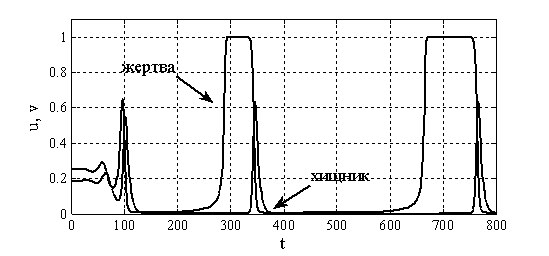
Рис. 2. Изменение функци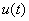й и 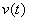от времени при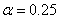
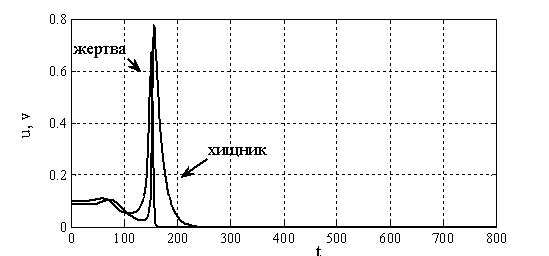
Рис. 3. Изменение функци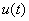й и 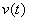от времени при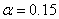 
Параметр 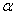во втором уравнении в (2) представляет собой удельную смертность хищника. Потому модель Базыкина — Свирежева в отличие от модели Лотка и Вольтерра «чувствительна» к смертности хищника. То есть, если в системе по каким-то причинам изменяется значение параметра 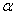, то в зависимости от ее текущего состояния, могут, либо возникнуть колебания (рис. 1), либо периодические «вспышки» численности (рис. 2). Возможна гибель хищника при высокой его удельной смертности, или гибель обеих популяций при малой удельной смертности хищника (рис. 3).
Полученные выше результаты относятся к «точечным» моделям. Поскольку реальные популяции живут на территориях, то учет пространственного распределения особей в математических моделях может привести к результатам не содержащихся в точечных моделях [5, 7, 13–17, 24, 29, 30, 37].
Математические методы, используемые при моделировании взаимодействующих популяций, можно использовать и при моделировании процессов, происходящих в физически, химически и биологически активных средах [3, 8, 9, 11, 12, 27, 38, 39]. Для оценки экономических последствий взаимоотношений в системе «хищник-жертва» можно использовать методы математической экономики [10,19, 21].
Работа частично поддержана грантом РФФИ 14–06–00326.
Литература:
1. Апонин Ю. М., Апонина Е. А. Математическая модель сообщества хищник — жертва с нижним порогом численности жертвы // Компьютерные исследования и моделирование. — 2009. — Т. 1. — № 1. — С. 51–56.
2. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
3. Балыкина Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.
4. Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в двух томах. М.: Мир, 1989. Т. 1. — 667 с. Т. 2. — 477с.
5. Будянский А. В., Цибулин В. Г. Моделирование пространственно-временной миграции близкородственных популяций // Компьютерные исследования и моделирование. — 2011. — Т. 3. — № 4. — С. 477–488.
6. Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. — 288 с.
7. Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вест. С.-Петерб. ун-та. Сер. 10. — 2012. — Вып. 4. — С. 18–30.
8. Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
9. Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
10. Колокольцов В. Н., Малафеев О. А. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть I) // Вестник гражданских инженеров. — 2010 — № 4 — С. 144–153.
11. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
12. Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2(61). — С. 19–24.
13. Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28–33.
14. Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
15. Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
16. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
17. Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
18. Коробченко М. А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. — 2009. — Т. 88. — № 4. — С. 465–472.
19. Малафеев О. А., Пахар О. В. Динамическая нестационарная задача инвестирования проектов в условиях конкуренции // Проблемы механики и управления: Нелинейные динамические системы. — 2009. — № 41. — С. 103–108.
20. Мамонтов С. Н. Распределение по стволу дерева короеда-типографа (ips typographus, coleoptera, scolyniddae) и его энтомогафов // Зоологический журнал. — 2009. — Т. 88. — № 9. — С. 1139–1145.
21. Миндлин Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
22. Мятлев В. Д., Панченко Л. А., Ризниченко Г. Ю., Терехин А. Т. Теория вероятностей и математическая статистика. Математические модели. М.: Издательский центр «Акадкмия», 2009. — 320 с.
23. Окулова Н. М., Катаев Г. Д. Взаимосвязи «хищник-красно-серая полевка» в сообществах позвоночных животных Лапландского заповедника // Зоологический журнал. — 2007. — Т. 86. — № 8. — С. 989–998.
24. Ризниченко Г. Ю., Рубин А. Б. Биофизическая динамика продукционных процессов. Москва — Ижевск: Институт компьютерных технологий, 2004. — 464 с.
25. Садыков О. Ф., Бененсон И. Е. Динамика численности мелких млекопитающих: Концепции, гипотезы, модели. М.: Наука, 1992. — 191 с.
26. Свирежев Ю. М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. М: Наука, 1987. — 368 с.
27. Тихонов А. Н., Самарский А. А. Уравнение математической физики. М.: Наука, 1972. — 735 с.
28. Трубецков Д. И. Феномен математической модели Лотки-Вольтерры и сходных с ней // Известия высших учебных заведений. Прикладная нелинейная динамика. — 2011. — Т. 19. — № 2. — С. 69–88.
29. Тютюнов Ю. В. Пространственная модель развития устойчивости насекомых-вредителей к трансгенной инсектицидной сельскохозяйственной культуре // Биофизика. — 2007. — Т. 52. — № 1. — С. 95–113.
30. Тютюнов Ю. В., Загребнева А. Д., Сурков Ф. А., Азовский А. И. Микромасштабная пятнистость распределения веслоногих рачков как результат трофически обусловленных миграций // Биофизика. — 2009. — Т. 54. — Вып. 3. — С. 508–514.
31. Уморин П. П. Роль хищников в устойчивом существовании нескольких видов водорослей // Биология внутренних вод. — 2009. — № 1. — С. 3–7.
32. Abrams P. A., Chad E., Brassil C. E., Robert D., Holt R. D. Dynamics and responses to mortality rates ofcompeting predators undergoing predator–prey cycles // Theoretical Population Biology. — 2003. — V. 64. — P. 163–176.
33. Garvie M. R. Finite-difference schemes for reaction–diffusion equations modeling predator–prey interactions in Matlab // Bulletin of Mathematical Biology. — 2007. — V. 69. — P. 931–956.
34. Ge w., Gui z. The effect of harvesting on a predator–prey system with stage structure // Ecological Modelling. — 2005. — V. 187. — P. 329–340.
35. Jones L. E., Ellner S. P Evolutionary Tradeoff and Equilibrium in an Aquatic Predator–Prey System // Bulletin of Mathematical Biology. — 2004. — V. 66. — P. 1547–1573.
36. Lopez-Sanchez J. F., Alhama F., Gonzalez-Fernandez C.F Introduction and permanence of species in a diffusive Lotka-Volterra system with time-dependent coefficients // Ecological Modelling. — 2005. — V. 183. P. 1–9.
37. Murray D. D. Mathematical biology. N. Y. Springer. 2002. — 551 p.
38. Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
39. Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — С. 361–364.
40. Wang W., Takeuchi Y.Adaptation of prey and predators between patches // Journal of Theoretical Biology. — 2009. — V. 258. — P. 603–613.
