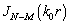В статье рассмотрен алгоритм UCA‑Root‑Rare, применяемый для однородной антенной решётки с кольцевой апертурой, предназначенный для оценивания азимута и угла места источников радиоизлучения. Алгоритм позволяет получить оценки азимута источников радиоизлучения отдельно от оценок угла места. Приведены результаты моделирования алгоритма. В рамках статьи рассмотрено только азимутальное оценивание.
Ключевые слова: UCA‑Root‑Rare, редукция ранга, пеленг, кольцевая антенная решётка
Введение. За последние 40 лет разработано и исследовано большое количество алгоритмов оценивания местоположения (ОМ) источников радиоизлучения (ИРИ). Возможность применения таких алгоритмов в реальных системах основывается на их вычислительной сложности и требованиях к геометрии антенной решётки (АР). Многие из алгоритмов, применяются только с АР определённой конфигурации, такие как однородные линейные АР и однородные кольцевые АР (ОКАР).
Среди алгоритмов ОМ ИРИ особое место занимают алгоритмы, основанные на разделении подпространств сигнала и шума. Наиболее популярным алгоритмом является алгоритм многосигнальной классификации или MUSIC (Multiple Signal Classification) [1,2]. Однако для приложений реального времени вычислительная сложность алгоритма MUSIC может оказаться неприемлемой, поскольку для получения оценок необходимо выполнить процедуру двухмерного поиска.
Наименьшей вычислительной сложностью среди алгоритмов, основанных на разделении подпространств сигнала и шума, обладают так называемые алгоритмы свободные от поиска. Первыми и, возможно, наиболее популярными алгоритмами подобного типа являются алгоритм Root‑MUSIC [3] и алгоритм ESPRIT [4]. Однако они могут быть применены только для определённого типа АР. В частности, алгоритм Root‑MUSIC может быть применён только к линейным АР, а алгоритм ESPRIT требует АР, состоящей из двух одинаковых и одинаково ориентированных подрешёток [5]. Для обоих этих алгоритмов были разработаны полезные обобщения для некоторых типов АР. В частности, для ОКАР были получены алгоритмы UCA‑Root‑MUSIC, UCA‑ESPRIT [6], алгоритм UCA‑Rare [7] и обобщенный ESPRIT [8].
Некоторые алгоритмы ОМ, применяемые с ОКАР, состоящей из ненаправленных элементов, среди которых UCA‑ESPRIT, привлекательны из‑за их простой реализации и способности обеспечивать автоматическое получение пары оценок азимута и угла места. Однако эти методы опираются на предположение о ненаправленности элементов. Алгоритм UCA‑Rare позволяет преодолеть предположение о ненаправленности элементов, тем самым допуская применение решёток, состоящих из произвольных, но идентичных, направленных элементов [7].
Цель работы — рассмотреть теоретические аспекты алгоритма UCA‑Root‑Rare и исследовать погрешность оценок местоположения ИРИ и их зависимость при различных параметрах ОКАР и отношении сигнал–шум.
1. Модель сигнала
Рассмотрим ОКАР из 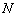 элементов, равномерно расположенных по окружности радиусом
элементов, равномерно расположенных по окружности радиусом 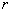 , изображённую на рисунке 1.
, изображённую на рисунке 1.
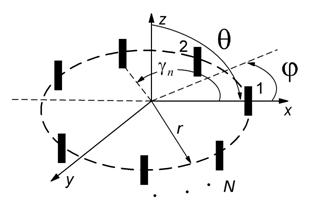
Рис. 1. Однородная кольцевая решётка
Предположим, что на АР, расположенную в дальней зоне относительно ИРИ, падают плоские волны, излучённые 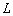 источниками. Неизвестные направления прихода волн характеризуются парами углов
источниками. Неизвестные направления прихода волн характеризуются парами углов 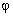 и
и 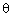 , где
, где 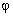 азимут,
азимут, 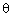 угол места. Угол места ИРИ
угол места. Угол места ИРИ 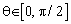 отсчитывается вниз по оси
отсчитывается вниз по оси 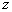 , а азимут
, а азимут 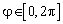 измеряется от оси
измеряется от оси 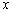 против часовой стрелки в плоскости
против часовой стрелки в плоскости 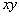 . Поскольку источников
. Поскольку источников 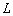 , то имеем набор из
, то имеем набор из 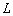 пар
пар 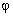 и
и 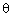 :
: 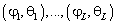 . Вектор отсчётов сигналов с АР в
. Вектор отсчётов сигналов с АР в 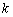 ‑ый момент времени, имеющий размерность
‑ый момент времени, имеющий размерность 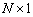 , может быть записан как:
, может быть записан как:
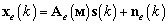 , (1)
, (1)
где 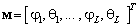 — вектор направлений, размером
— вектор направлений, размером 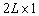 ;
; 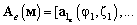
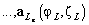 — матрица отклика ОКАР в пространстве элементов, размером
— матрица отклика ОКАР в пространстве элементов, размером 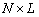 , состоящая из
, состоящая из 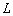 векторов отклика
векторов отклика 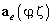 :
:
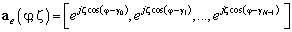 , (2)
, (2)
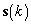 — вектор сигналов от различных ИРИ в
— вектор сигналов от различных ИРИ в 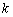 ‑ый момент времени, размером
‑ый момент времени, размером 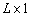 ;
; 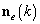 — вектор отсчётов шума с
— вектор отсчётов шума с 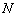 элементов решётки в
элементов решётки в 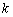 ‑ый момент времени, размером
‑ый момент времени, размером 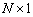 ;
; 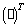 знак транспонирования, нижний индекс
знак транспонирования, нижний индекс 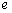 обозначает, что пока все операции проводятся в пространстве элементов (см. далее).
обозначает, что пока все операции проводятся в пространстве элементов (см. далее).
Вектор 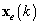 содержит отсчёты доступные алгоритму в качестве входных данных. Тогда для
содержит отсчёты доступные алгоритму в качестве входных данных. Тогда для 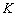 отсчётов
отсчётов 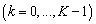 получим матрицу
получим матрицу 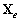 , размером
, размером 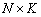 , содержащую набор из
, содержащую набор из 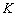 векторов
векторов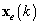 :
:
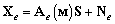 , (3)
, (3)
где 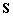 — это
— это 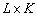 сигнальная матрица,
сигнальная матрица, 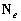 матрица шума размером
матрица шума размером 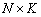 .
.
Алгоритм UCA‑Root‑Rare является обобщением алгоритма Root‑MUSIC для случая частично калиброванных антенных решёток. Алгоритм Root‑MUSIC был разработан для применения с однородными линейными решётками [5], поэтому он не может быть напрямую применён к ОКАР. Однако был предложен метод, позволяющий косвенным путём применить Root‑MUSIC не непосредственно к ОКАР, а к виртуальной проекции ОКАР или к так называемой виртуальной линейно АР, используя метод возбуждения фазовых мод [6,9], также называемым переходом в пространство лучей.
2. Переход в пространство лучей
В этой части статьи, описывается режим или принцип возбуждения фазовых мод [6,9]. Преобразование в пространство лучей, описываемое в этом разделе, основано на режиме возбуждения фазовых мод.
2.А Непрерывная кольцевая апертура
В случае непрерывной кольцевой апертуры, любая возбуждающая функция является периодической с периодом 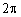 и поэтому может быть представлена рядом Фурье [6,9,10]. Произвольная функция возбуждения
и поэтому может быть представлена рядом Фурье [6,9,10]. Произвольная функция возбуждения 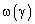 , которая может быть представлена как
, которая может быть представлена как 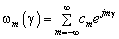 , где
, где 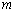 ‑ая фазовая мода
‑ая фазовая мода 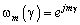 — это пространственная гармоника возбуждённой решётки, а
— это пространственная гармоника возбуждённой решётки, а 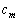 — соответствующий коэффициент ряда Фурье. Интегрируя пространственную гармонику
— соответствующий коэффициент ряда Фурье. Интегрируя пространственную гармонику 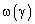 по всей апертуре решётки, мы можем вычислить нормированную диаграмму направленности в дальней зоне
по всей апертуре решётки, мы можем вычислить нормированную диаграмму направленности в дальней зоне 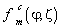 , которая для заданной апертуры для
, которая для заданной апертуры для 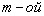 фазовой моды имеет вид [6]:
фазовой моды имеет вид [6]:
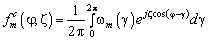 , (4)
, (4)
где верхний индекс 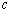 означает непрерывную апертуру.
означает непрерывную апертуру.
Выражение (4) также может быть представлено с помощью функции Бесселя [9]:
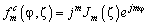 , (5)
, (5)
где 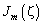 — функция Бесселя первого рода порядка
— функция Бесселя первого рода порядка 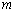 . Поскольку
. Поскольку 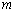 ‑ая фазовая мода пропорциональна функции Бесселя первого рода
‑ая фазовая мода пропорциональна функции Бесселя первого рода 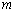 ‑го порядка, имеющей убывающий, в зависимости от порядка, характер, в области определения
‑го порядка, имеющей убывающий, в зависимости от порядка, характер, в области определения 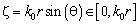 может возбуждаться только конечное число мод, имеющих достаточную силу [9].
может возбуждаться только конечное число мод, имеющих достаточную силу [9].
Обозначим через 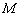 наивысший порядок моды, возбуждающейся в решётке с достаточной силой. Правило определения
наивысший порядок моды, возбуждающейся в решётке с достаточной силой. Правило определения 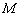 [9]:
[9]:
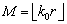 , (6)
, (6)
где 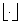 определяет целую часть.
определяет целую часть.
Для наглядного изображения этого свойства, рассмотрим ОКАР радиусом 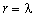 . Выражение (6) предполагает, что максимальный порядок моды
. Выражение (6) предполагает, что максимальный порядок моды 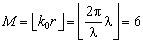 . На рисунке 2 отображены функции Бесселя первого рода порядка
. На рисунке 2 отображены функции Бесселя первого рода порядка 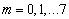 . Как видно из приведённых графиков, значение функции Бесселя 7 порядка
. Как видно из приведённых графиков, значение функции Бесселя 7 порядка 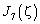 мало в области определения
мало в области определения 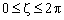 . Тогда согласно (6), следует ограничить порядок фазовых мод до значений
. Тогда согласно (6), следует ограничить порядок фазовых мод до значений 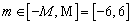 .
.
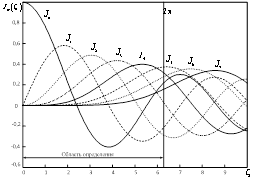
Рис. 2. Функции Бесселя первого рода порядка 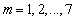 .
.
2.Б Дискретная ОКАР
Дискретный вариант ОКАР — это случай кольцевой АР с непрерывной апертурой при конечном количестве 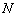 элементов АР, равномерно распределённых по всей длине окружности, как показано на рисунке 1.
элементов АР, равномерно распределённых по всей длине окружности, как показано на рисунке 1.
Для ОКАР, нормированный весовой вектор в пространстве лучей, который возбуждает решётку фазовой модой порядка 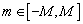 , записывается как
, записывается как
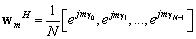 , (7)
, (7)
где 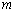 — порядок возбуждающей моды,
— порядок возбуждающей моды, 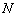 — количество антенных элементов,
— количество антенных элементов, 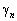 — угловое положение
— угловое положение 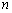 ‑го элемента,
‑го элемента, 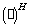 — знак комплексного сопряжения и транспонирования. Следовательно, диаграмма направленности может быть записана как
— знак комплексного сопряжения и транспонирования. Следовательно, диаграмма направленности может быть записана как
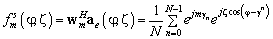 , (8)
, (8)
где 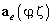 — это вектор отклика в пространстве элементов (2), верхний индекс
— это вектор отклика в пространстве элементов (2), верхний индекс 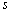 обозначает дискретную ОКАР. Для моды порядка
обозначает дискретную ОКАР. Для моды порядка 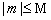 , выражение (8) может быть переписано:
, выражение (8) может быть переписано:
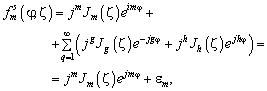 (9)
(9)
где 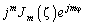 — основная компонента, идентичная описанию диаграммы направленности АР в дальней зоне для непрерывной АР;
— основная компонента, идентичная описанию диаграммы направленности АР в дальней зоне для непрерывной АР; 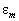 — остаточная компонента, возникающая из‑за дискретизации непрерывной апертуры на
— остаточная компонента, возникающая из‑за дискретизации непрерывной апертуры на 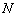 элементов,
элементов, 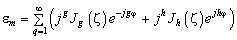 ;
;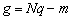 и
и 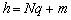 . Величину
. Величину 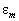 необходимо минимизировать для получения максимально приближенных к идеальным (при непрерывной апертуре) характеристикам [6].
необходимо минимизировать для получения максимально приближенных к идеальным (при непрерывной апертуре) характеристикам [6].
Проведённое в [6] исследование формулы (9) показывает, что для того, чтобы влияние остаточной компоненты было минимальным, необходимо выполнить условие:
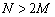 . (10)
. (10)
Рассмотрим влияние количества элементов решётки 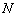 на величину остаточной компоненты. Наибольший вес среди всех остаточных компонент имеет компонента с индексом
на величину остаточной компоненты. Наибольший вес среди всех остаточных компонент имеет компонента с индексом 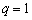 , а её амплитуда выражается функцией Бесселя порядка
, а её амплитуда выражается функцией Бесселя порядка 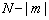 , где
, где 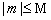 . Очевидно, что её значение максимально для моды порядка
. Очевидно, что её значение максимально для моды порядка 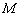 , а её амплитуда равняется
, а её амплитуда равняется 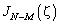 . С увеличением порядка, функция
. С увеличением порядка, функция 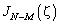 становится монотонно возрастающей в области определения
становится монотонно возрастающей в области определения 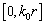 (см.
(см. 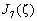 на рисунке 2). Выбирая число
на рисунке 2). Выбирая число 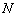 элементов решётки, можно уменьшить вес и влияние остаточной компоненты.
элементов решётки, можно уменьшить вес и влияние остаточной компоненты.
Рассмотрим решётку радиусом 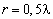 , и посмотрим на значение остаточной компоненты с индексом
, и посмотрим на значение остаточной компоненты с индексом 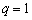 , амплитуда которой равна
, амплитуда которой равна 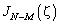 , количество элементов решётки будем изменять. Область определения
, количество элементов решётки будем изменять. Область определения 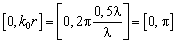 , максимальный порядок моды
, максимальный порядок моды 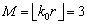 .
.
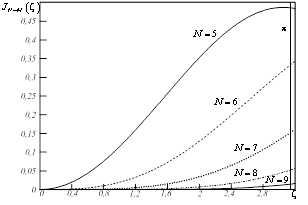
Рис.к 3. Функции Бесселя первого рода, порядка 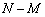 для ОКАР радиусом
для ОКАР радиусом 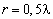 при различном количестве элементов
при различном количестве элементов 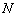
На рисунке 3 показаны соответствующие функции Бесселя для рассматриваемой ОКАР. Как видно из рисунка 3, значение остаточной компоненты с индексом 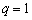 резко (с 0,485 до 0,015) уменьшается при увеличении количества элементов решётки
резко (с 0,485 до 0,015) уменьшается при увеличении количества элементов решётки 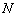 . В таблице 1 приведены соответствующие значения остаточной компоненты на границе области определения при различном количестве элементов ОКАР.
. В таблице 1 приведены соответствующие значения остаточной компоненты на границе области определения при различном количестве элементов ОКАР.
Таблица 1
Зависимость остаточной компоненты от количества элементов решётки
|
Количество элементов ОКАР |
Значение остаточной компоненты |
|
5 |
0,485 |
|
6 |
0,333 |
|
7 |
0,151 |
|
8 |
0,052 |
|
9 |
0,015 |
3. Алгоритм UCA‑Root‑Rare
Как говорилось ранее, алгоритм UCA‑Root‑Rare является обобщением алгоритма Root‑MUSIC, который в свою очередь основан на разделения подпространств сигнала и шума ковариационной матрицы. Однако для применения алгоритма UCA‑Root‑Rare к ОКАР необходимо выполнить преобразование в пространство лучей. Таким образом, можно записать следующие этапы алгоритма UCA‑Root‑Rare.
Этапы выполнения алгоритма:
Шаг 1. Переход из пространства элементов в пространство лучей
Преобразование в пространство лучей осуществляется с помощью умножения вектора 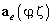 и матрицы данных
и матрицы данных 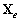 из пространства элементов на матрицу дискретного преобразования Фурье
из пространства элементов на матрицу дискретного преобразования Фурье 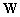 , размером
, размером 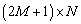 ,
, 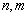 ‑ый элемент которой равен
‑ый элемент которой равен 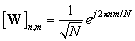 ,
, 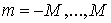 ,
, 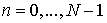 . Тогда,
. Тогда, 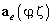 преобразуется в вектор:
преобразуется в вектор:
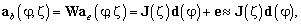 (11)
(11)
где 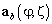 — вектор отклика ОКАР в пространстве лучей, размером
— вектор отклика ОКАР в пространстве лучей, размером 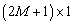 , нижний индекс
, нижний индекс 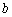 показывает, что обработка ведётся в пространстве лучей.
показывает, что обработка ведётся в пространстве лучей.
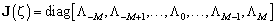 , (12)
, (12)
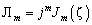 ; (13)
; (13)
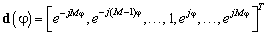 . (14)
. (14)
Вектор 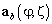 может быть разложен на составляющие:
может быть разложен на составляющие:
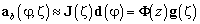 , (15)
, (15)
где
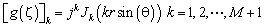 , (16)
, (16)
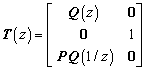 (17)
(17)
размера 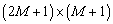 ,
,
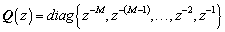 (18)
(18)
размера 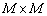 ,
,
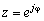 . (19)
. (19)
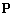 — это
— это 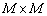 матрица отражений:
матрица отражений:
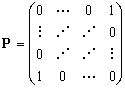 . (20)
. (20)
Теперь произведём отображение матрицы данных 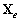 из пространства элементов в матрицу данных в пространстве лучей:
из пространства элементов в матрицу данных в пространстве лучей:
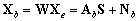 , (21)
, (21)
где 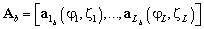 — матрица отклика в пространстве лучей,
— матрица отклика в пространстве лучей, 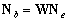 матрица белого шума в пространстве лучей, размером
матрица белого шума в пространстве лучей, размером 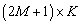 .
.
Шаг 2. Вычисление ковариационной матрицы
Вычисление оценки ковариационной матрицы 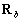 в пространстве лучей выполняется следующим образом:
в пространстве лучей выполняется следующим образом:
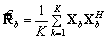 . (22)
. (22)
Шаг 3. Получение подпространств сигнала и шума.
Выполним разложение матрицы 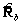 и выделим подпространство сигнала и подпространство шума [11]:
и выделим подпространство сигнала и подпространство шума [11]:
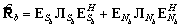 , (23)
, (23)
где собственные значения 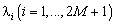 сортированы в порядке убывания
сортированы в порядке убывания 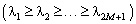 ,
, 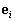 — собственные вектора соответствующие собственным значениям, а матрицы
— собственные вектора соответствующие собственным значениям, а матрицы 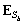 и
и 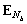 соответствуют подпространству сигнала и подпространству шума соответственно, причем
соответствуют подпространству сигнала и подпространству шума соответственно, причем 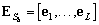 , а
, а 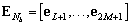 ,
, 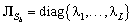 диагональная матрица из
диагональная матрица из 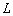 наибольших собственных чисел матрицы
наибольших собственных чисел матрицы 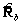 , соответствующая сигнальному подпространству,
, соответствующая сигнальному подпространству, 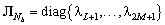 диагональная матрица из
диагональная матрица из 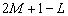 оставшихся собственных значений матрицы
оставшихся собственных значений матрицы 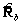 , соответствующая шумовому подпространству.
, соответствующая шумовому подпространству.
Шаг 4. Оценивание азимута
Рассмотрим алгоритм MUSIC в пространстве лучей. Получение оценок местоположения такой функцией соответствует двухмерному поиску 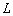 минимумов функции:
минимумов функции:
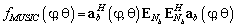 . (24)
. (24)
Заменяя 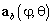 выражением (15) получим:
выражением (15) получим:
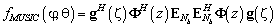 . (25)
. (25)
В случае если бы углы места были известны ИРИ, то функцию MUSIC 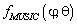 можно было бы представить как полином с
можно было бы представить как полином с 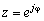 , а для получения оценок азимута можно было бы применить вычислительно эффективный алгоритм Root‑MUSIC. Но на практике, получение априорной информации об угле места ИРИ не всегда возможно. Разложение на множители вектора
, а для получения оценок азимута можно было бы применить вычислительно эффективный алгоритм Root‑MUSIC. Но на практике, получение априорной информации об угле места ИРИ не всегда возможно. Разложение на множители вектора 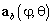 (15) позволяет применить алгоритмUCA‑Root‑Rare. Идея алгоритма заключается в том, чтобы частично разрешить проблему поиска минимумов функции (25), расширяя множество возможных решений в исходном пространстве до множества решений в так называемое Rare пространстве
(15) позволяет применить алгоритмUCA‑Root‑Rare. Идея алгоритма заключается в том, чтобы частично разрешить проблему поиска минимумов функции (25), расширяя множество возможных решений в исходном пространстве до множества решений в так называемое Rare пространстве 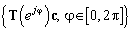 , где
, где 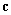 — это произвольный комплексный вектор, размером
— это произвольный комплексный вектор, размером 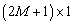 . Перепишем выражение (25):
. Перепишем выражение (25):
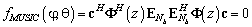 . (26)
. (26)
Алгоритм UCA‑RARE использует особенность выражения (26), заключающуюся в том, что оно содержит только информацию об азимуте ИРИ. Поскольку произвольный вектор 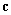 не может быть нулевым, то можно записать
не может быть нулевым, то можно записать
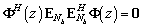 . (27)
. (27)
Получение оценок азимута получается независимо от оценок угла места, путем вычисления нулей (27). Это выражение может быть сведено к одномерному полиномиальному критерию [7]
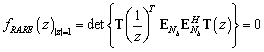 . (28)
. (28)
Результаты моделирования получения оценок азимута по выражению (28) приведены в экспериментальной части.
4. Экспериментальные исследования.
Рассмотрим ОКАР с количеством элементов 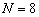 , радиусом
, радиусом 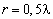 . Предположим, что излучают три некоррелированных источника, с координатами
. Предположим, что излучают три некоррелированных источника, с координатами 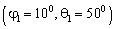 ,
, 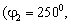
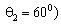 и
и 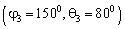 . Количество выборок сигнала с каждого элемента ОКАР
. Количество выборок сигнала с каждого элемента ОКАР 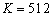 .
.
На рисунке 4 приведены получаемые алгоритмом UCA‑Root‑Rare азимутальные оценки местоположения (корни полиномиального выражения (28)) отмеченные кружками. Крестиками отмечены истинные координаты ИРИ, пунктиром показана единичная окружность. Согласно рисунку 4, помимо оценок, соответствующих истинным положениям ИРИ, присутствуют также зеркальные оценки, отстоящие от истинных на 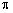 , и паразитные.
, и паразитные.
Проведем численный анализ смещения оценок азимута от их истинных значений при различных конфигурациях ОКАР, а также при различных отношениях сигнал‑шум. Предполагается, что устранены все зеркальные и паразитные оценки. Полученные оценки являются средним арифметическим модулей смещения оценок трех источников, измеренных по 300 запускам алгоритма. Моделируются источники, параметры которых приведены выше.

Рис. 4.Оценки местоположения ИРИ, полученные алгоритмом UCA‑RARE. 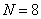 , отношение сигнал‑шум 25 дБ
, отношение сигнал‑шум 25 дБ
На рисунке 5 представлена зависимость модуля смещения оценок, от истинного значения местоположения ИРИ при фиксированном радиусе ОКАР 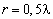 .
.
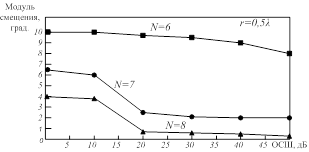
Рис. 5. Модуль смещения оценок азимута ИРИ, при различном количестве элементов ОКАР 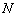 и отношении сигнал‑шум; радиус решётки
и отношении сигнал‑шум; радиус решётки 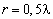
Как видно из рисунка 5 наибольшим смещением обладает конфигурация ОКАР, содержащая 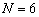 элементов, а при увеличении количества элементов, смещение уменьшается. При малом количестве элементов решётки становится заметным влияние остаточной компоненты, что частично объясняет ухудшение определения места положения ИРИ при уменьшении количества элементов в АР.
элементов, а при увеличении количества элементов, смещение уменьшается. При малом количестве элементов решётки становится заметным влияние остаточной компоненты, что частично объясняет ухудшение определения места положения ИРИ при уменьшении количества элементов в АР.
На рисунке 6 показаны зависимости величины модуля смещения при фиксированном количестве элементов решётки 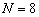 и различном радиусе ОКАР.
и различном радиусе ОКАР.
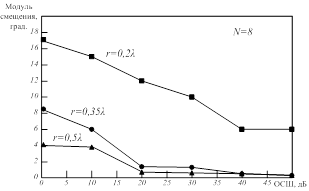
Рис. 6. Модуль смещения оценок местоположения ИРИ при различных значениях радиуса ОКАР и отношениях сигнал‑шум (ОСШ); количество элементов 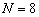
Согласно рисунку 6, уменьшение радиуса ОКАР негативно сказывается на точности определения оценок. С увеличением радиуса точность оценок взрастает. При работе в области высокого отношения сигнал‑шум (более 20 дБ) точность для решётки радиусом 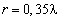 и
и 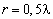 практически одинакова.
практически одинакова.
5. Заключение
В статье описывается алгоритм UCA‑Root‑Rare, позволяющий получить оценки местоположения множественных узкополосных ИРИ при применении ОКАР. Показано, что в отличие от популярного алгоритма MUSIC, требующуего выполнения двухмерного поиска, алгоритм UCA‑RARE выполняет одномерный поиск оценок местоположения, путём вычисления корней полиномиального выражения (28). К сожалению, эти оценки содержат паразитные и зеркальные оценки, методы устранения которых требуют повышения вычислительных затрат.
Показано, что использование ОКАР с малым количеством элементов 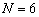 и менее не целесообразно для данного алгоритма, поскольку получаемые оценки имеют смещение
и менее не целесообразно для данного алгоритма, поскольку получаемые оценки имеют смещение 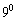 даже при высоких (30 дБ и более) отношениях сигнал‑шум.
даже при высоких (30 дБ и более) отношениях сигнал‑шум.
Также показано, что при малом радиусе антенной решётки (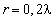 ) смещение оценок составляет не менее
) смещение оценок составляет не менее 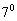 даже при отношении сигнал‑шум 40–50 дБ.
даже при отношении сигнал‑шум 40–50 дБ.
Достоинствами данного алгоритма является независимое от угла места получение оценок азимута ИРИ.
Литература:
1. Schmidt R. O. Multiple Emitter Location and Signal Parameter Estimation // IEEE Antennas and Propagation. 1986. Vol. AP-34. P. 276–280.
2. Barabell A. Improving the resolution performance of eigenstructure-based direction-finding algorithms // ICASSP. 1983. P. 336‑339.
3. Friedlander B. The root-MUSIC algorithm for direction finding with interpolated arrays // Europe Journal Signal Processing. 1993. No 30. P. 15–29.
4. Roy R., Kailath T. ESPRIT: estimation of signal parameters via rotational invariance techniques // IEEE Acoustics, Speech and Signal Processing. 1989. No 37(7). P. 984–995.
5. Tuncer E., Friedlander B. Classical and Modern Directional-of-Arrival Estimation. Burlington: Academic Press, 2009. 400 p.
6. Mathews C. P., Zoltowski M. D. Eigenstructure techniques for 2-D angle estimation with uniform circular arrays // IEEE Signal Processing. 1994. No 42(9). P. 2395–2407.
7. Pesavento M., Böhme J. F. Direction of arrival estimation in uniform circular arrays composed of directional elements // Sensor Array and Multichannel Signal Processing Workshop. 2002. No 8. P. 503–507.
8. Gao F., Gershman A. B. A generalized ESPRIT approach to direction-of-arrival estimation // IEEE Signal Processing. 2005. No 12(3). P. 254‑257.
9. Davis D. E. N. The Handbook of Antenna Design. London: Peregrinus, 1983.Vol. 2.
10. Belloni F., Richter A., Koivunen V. Reducing excess variance in beamspace methods for uniform circular array // IEEE Statistical Signal Processing Workshop. 2005. No 7. P. 17–20.
11. Marple L. Digital spectral analysis with applications. New Jersey: Prentice-Hall, 1987. P. 492.