Рассмотрены методы пеленгования источников излучения (ИИ), основанные на анализе корреляционной матрицы принятых сигналов, анализе собственных значений и собственных векторов корреляционной матрицы. Приведено поэтапное описание шагов выполнения алгоритмов, а также результаты численного моделирования. В рамках статьи рассмотрены только алгоритмы, требующие выполнение полного двухмерного поиска по координатам азимута и угла места.
Ключевые слова: MUSIC, AAR, Кейпон, MEM, MLM, пеленг, кольцевая антенная решётка
Введение. Во многих приложениях, связанных с обработкой сигналов с антенных решёток, таких как радиолокация, гидролокация и беспроводная связь, интересующая нас информация о местоположении ИИ извлекается из принимаемых волн, излученных источником. Проблема оценивания координат ИИ при помощи корреляционных алгоритмов привлекает внимание разработчиков и исследователей последние несколько десятилетий.
Корреляционные алгоритмы пеленгования могут быть разделены на два класса по количеству затрачиваемых ресурсов вычислительной системы и времени выполнения. К первому, «медленному» классу, можно отнести алгоритмы, требующие повышенных вычислительных затрат вызванных необходимостью выполнением полного двухмерного поиска по обеим координатам азимута и угла места. Сюда можно отнести такие алгоритмы как: алгоритм сканирования лучом (Beam Scan Algorithm (BSA)), алгоритм Кейпона (Capon) [1], алгоритм теплового шума (Thermal Noise Algorithm (TNA)) [2], обобщенный метод Кейпона [3], алгоритм многосигнальной классификации (Multiple Signal Classification (MUSIC)) [4] и др. Ко второму, «быстрому» классу алгоритмов, требующих меньше вычислительных затрат, можно отнести алгоритмы, избегающие выполнения полного двухмерного поиска. Обычно такие алгоритмы являются численно и вычислительно эффективными модификациями алгоритмов «медленного» класса. К таким алгоритма можно отнести: модификации алгоритмов основанные на вычислении корней, например Root‑MUSIC, алгоритм оценивания параметров через инвариант вращения (ESPRIT), алгоритмы редукции ранга (Rank Reduction (RARE)), например UCA‑RARE.
Цель статьи — демонстрация поиска координат ИИ при помощи некоторых алгоритмов «медленного» класса при применении однородной кольцевой антенной решётки (ОКАР).
1. Модель сигнала. Рассмотрим ОКАР из 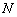 элементов, равномерно расположенных по окружности радиусом
элементов, равномерно расположенных по окружности радиусом 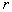 , изображённую на рисунке 1.
, изображённую на рисунке 1.
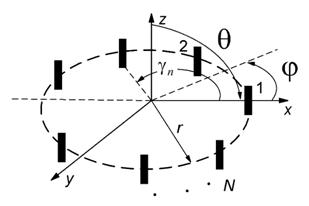
Рис. 1. Однородная кольцевая решётка
Предположим, что на АР, расположенную в дальней зоне относительно ИРИ, падают плоские волны, излучённые 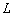 источниками. Неизвестные координаты источников излучения характеризуются парами углов
источниками. Неизвестные координаты источников излучения характеризуются парами углов 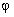 и
и 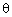 , где
, где 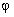 азимут,
азимут, 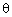 угол места. Угол места ИИ
угол места. Угол места ИИ 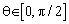 отсчитывается вниз по оси
отсчитывается вниз по оси 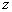 , а азимут
, а азимут 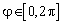 измеряется от оси
измеряется от оси 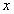 против часовой стрелки в плоскости
против часовой стрелки в плоскости 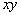 . Поскольку источников
. Поскольку источников 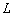 , то имеем набор из
, то имеем набор из 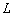 пар
пар 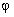 и
и 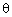 :
: 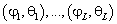 . Вектор отсчётов сигналов с АР в
. Вектор отсчётов сигналов с АР в 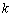 ‑ый момент времени, имеющий размерность
‑ый момент времени, имеющий размерность 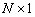 , может быть записан как:
, может быть записан как:
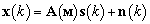 , (1)
, (1)
где 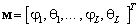 — вектор направлений, размером
— вектор направлений, размером 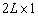 ;
; 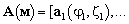
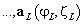 — матрица отклика ОКАР в пространстве элементов, размера
— матрица отклика ОКАР в пространстве элементов, размера 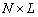 , состоящая из
, состоящая из 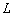 векторов отклика
векторов отклика 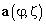 :
:
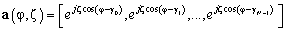 ; (2)
; (2)
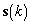 — вектор сигналов от различных ИРИ в
— вектор сигналов от различных ИРИ в 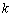 ‑ый момент времени, размера
‑ый момент времени, размера 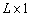 ;
; 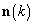 — вектор отсчётов шума с
— вектор отсчётов шума с 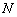 элементов решётки в
элементов решётки в 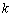 ‑ый момент времени, размером
‑ый момент времени, размером 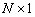 ;
; 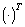 знак транспонирования.
знак транспонирования.
Все приведённые ниже алгоритмы работают с корреляционной матрицей сигнала, которая может быть вычислена как:
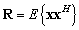 , (3)
, (3)
где 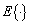 определяет математическое ожидание величины, стоящей в скобках.
определяет математическое ожидание величины, стоящей в скобках.
2. Алгоритмы. Ниже представлены некоторые алгоритмы «медленного» класса в порядке возрастания вычислительной сложности. При выполнении численного моделирования были приняты следующие допущения: шум предполагался аддитивным гауссовским случайным процессом с нулевым средним значением, отношение сигнал‑шум составляло 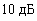 , расстояние между антенными элементами составляло
, расстояние между антенными элементами составляло 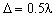 , число антенных элементов
, число антенных элементов 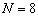 , число отсчётов сигнала с каждого элемента ОКАР составляло
, число отсчётов сигнала с каждого элемента ОКАР составляло 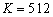 , предполагалось, что излучал один источник
, предполагалось, что излучал один источник 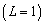 , имеющий координаты
, имеющий координаты 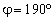 и
и 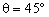 . Все спектральные характеристики нормированы к 1. Приведённые зависимости вычислялись при фиксированных углах
. Все спектральные характеристики нормированы к 1. Приведённые зависимости вычислялись при фиксированных углах 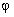 и
и 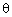 , а пример двухмерного углового спектра, полученного алгоритмом MUSIC, приведён на рисунке 2.
, а пример двухмерного углового спектра, полученного алгоритмом MUSIC, приведён на рисунке 2.
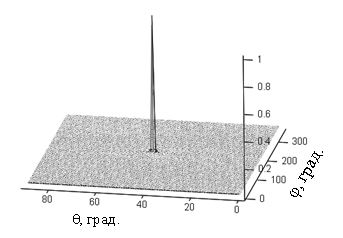
Рис. 2. Нормированный двухмерный угловой спектр алгоритма MUSIC
2.А. Алгоритм сканирования лучом (BSA)
BSA алгоритм выполняет поиск координат ИИ при помощи следующей функции
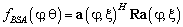 , (4)
, (4)
Соответствующие графики функции (4) приведены на рисунке 3.
Из графиков, приведённых на рисунке 3, видно, что угловой спектр является достаточно широким и в случае наличия нескольких близкорасположенных ИИ алгоритм BSA не сможет дать адекватных оценок их координат.
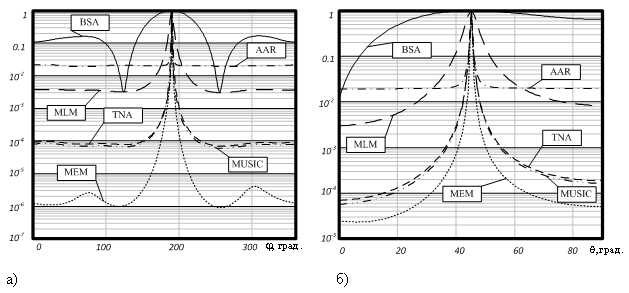
Рис. 3. Нормированный угловой спектр различных корреляционных методов пеленгования: а) спектр по азимуту, б) спектр по углу места
2.Б. Алгоритм Кейпона
Алгоритм Кейпона или как его часто называют метод максимального правдоподобия (Maximum Likelihood Method (MLM)) был предложен в 1969 году и относится к классу “сверхразрешающих”. Используя аналогию частотного и пространственного спектров, метод был предложен также для оценивания координат ИИ сигналов при помощи антенных решёток:
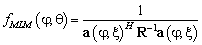 , (5)
, (5)
Из рисунка 3 следует, что алгоритм Кейпона обладает значительно более лучшим разрешением, чем алгоритм BSA. Антенная решётка (АР), оптимизированная по критерию Кейпона, стремится подавить любой сигнал, волновой фронт которого отличается от 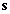 . Средняя мощность на выходе АР получается минимальной везде, кроме углов вблизи направлений на ИИ. Непосредственно в направлении на ИИ функция
. Средняя мощность на выходе АР получается минимальной везде, кроме углов вблизи направлений на ИИ. Непосредственно в направлении на ИИ функция 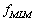 имеет максимум [3].
имеет максимум [3].
2.В. Алгоритм теплового шума.
Вскоре после появления метода Кейпона был предложен так называемый метод теплового шума TNA. Идея метода опирается на свойства АР, критерием эффективности которой является величина отношения мощности сигнала к средней суммарной мощности внешней помехи и собственного шума на выходе АР. В качестве функции, которая обеспечивает угловое разрешение в методе TNA, рассматривается величина, обратная мощности собственного шума [3]:
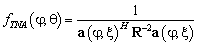 , (6)
, (6)
Соответствующий угловой спектр функции 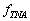 приведён на рисунке 3.
приведён на рисунке 3.
2 Г. Обобщенный метод Кейпона
Очевидно, что методы Кейпона и теплового шума могут быть рассмотрены с единой точки зрения и на основе этого могут быть предложены новые методы свехразрешения. Можно ожидать, что функции вида
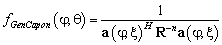 , (7)
, (7)
при 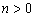 будут обладать повышенной эффективностью углового разрешения по сравнению с обычным методом сканирования лучом антенны.
будут обладать повышенной эффективностью углового разрешения по сравнению с обычным методом сканирования лучом антенны.
2.Д. Метод максимальной энтропии
В 1967 году Джон Бург (Burg) пошатнул основы обычного временного спектрального анализа с его предположением, что традиционное спектральное оценивание по существу было бесполезным. Он был недоволен тем фактом, что во времени, все общепризнанные методы для вычисления спектральной плотности мощности полностью ограничивается корреляционными задержками. Как альтернативу, Бург предложил его, теперь известный, метод спектрального оценивая или метод максимальной энтропии (Maximum Entropy Method (MEM)) [5]. Модификация метода максимальной энтропии для задачи пеленгования ИИ записывается как:
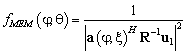 , (8)
, (8)
где 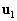 — это первый столбец единичной матрицы. Угловой спектр по методу максимальной энтропии приведён на рисунке 3.
— это первый столбец единичной матрицы. Угловой спектр по методу максимальной энтропии приведён на рисунке 3.
2.Е. Алгоритм адаптивной угловой характеристики.
Алгоритм Adapted Angular Response (AAR) был предложен Боргиотти (Borgiotti) и Капланом (Kaplan) [6]. Он может интерпретироваться как вариация алгоритма максимального правдоподобия. Спектральные оценки алгоритма AAR получаются масштабированием или взвешиванием спектральных оценок по методу максимального правдоподобия, так, что сумма квадратов амплитуд весовых коэффициентов принимала некоторое фиксированное значение. Вычисление углового спектра по методу AAR проводится при помощи следующего выражения:
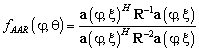 . (9)
. (9)
Угловой спектр алгоритма AAR приведён на рисунке 3.
2.Ж. Алгоритм многосигнальной классификации
Алгоритм MUSIC впервые был предложен Шмидтом (Shmidt) в 1979 году. Подход многосигнальной классификации для своего применения, помимо вычисления корреляционной матрицы, требует её разложения на собственные вектора и собственные числа с последующим выделением подпространств сигнала и шума. Этапы вычисления углового спектра по алгоритму MUSIC приведены в таблице 1, а соответствующий угловой спектр приведён на рисунках 1 и 3.
Таблица 1
Этапы выполнения алгоритма MUSIC
|
1. |
Получить корреляционную матрицу по формуле (3). |
|
2. |
Вычислить собственные значения корреляционной матрицы |
|
3. |
Вычислить собственный вектор |
|
4. |
Выделить подпространство шума |
|
5. |
Вычислить угловой спектр по формуле (10) |
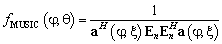 (10)
(10)
В общем, из рисунка 3 следует, что наилучшими характеристиками обладает метод максимальной энтропии MEM, нижняя граница которого примерно на два порядка ниже, чем у наиболее популярного алгоритма многосигнальной классификации (MUSIC). К тому же, MEM алгоритм не требует процедур, связанных с нахождением подпространств сигнала и шума. Дополнительным преимуществом при этом является то, что не нужно оценивать число ИИ, пеленгуемых ОКАР. Для алгоритма MUSIC неверная оценка числа ИИ в системе может привести к его полной неработоспособности или появлению в спектре паразитных пиков, которые могут быть приняты за ИИ. Остальные предлагаемые алгоритмы, также дают хорошие оценки координат ИИ, за исключением алгоритма BSA.
Заключение. Встатье были рассмотрены несколько корреляционных алгоритмов нахождения углового спектра. Проведено численное моделирование алгоритмов для случая пеленгования одного ИИ при использовании ОКАР, состоящей из 8 элементов, при сравнительно низком отношении сигнал шум, равным 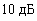 .
.
Литература:
1. J. Capon, «High-Resolution Frequency-Wavenumber Spectrum Analysis»,Proc. IEEE, 57, 1408 (1969).
2. W. Gabriel, «Spectral Analysis and Adaptive Array Superresolution Techniques», Proc. IEEE, 68, 654 (1980).
3. Ермолаев В. Т., Флаксман А. Г. Методы оценивания параметров источников сигналов и помех, принимаемых антенной решеткой. Учебно-методический материал по программе повышения квалификации «Новые подходы к проблемам генерации, обработки, передачи, хранения, защиты информации и их применение». Нижний Новгород, 2007, 98 с.
4. R. Schmidt, «Multiple Emitter Location and Signal Parameter Estimation»,Proc. RADC Spectrum Estimation Workshop, Rome, NY, 1979.
5. J. P. Burg, «Maximum Entropy Spectral Analysis», Proc. 37th Annual Meeting of the Society of Exploration Geophysicists, Oklahoma City, Oct. 31, 1967.
6. G. V. Borgiotti and L. J. Kaplan, «Super resolution of Uncorrelated Interference Sources by Using Adaptive Array Techniques», Trans. Antennas Propagation, AP-27, 842 (1979).







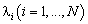 и сортировать их в порядке убывания
и сортировать их в порядке убывания 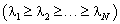 .
.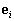 корреляционной матрицы для каждого собственного значения.
корреляционной матрицы для каждого собственного значения.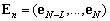 . Подпространство шума образуют собственные вектора, соответствующие
. Подпространство шума образуют собственные вектора, соответствующие 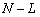 наименьшим собственным значениям
наименьшим собственным значениям